НАХОЖДЕНИЕ  ОПТИМАЛЬНОГО  ТУРИСТИЧЕСКОГО  МАРШРУТА

Варламова  Анна  Александровна

Хантова  Анна  Дмитриевна

студенты  3  курса,  факультет  информатики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

E -mail:  varlamova.anna.95@mail.ru

Тишин  Владимир  Викторович

научный  руководитель,  доцент,  кафедра  прикладной  математики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

Введение

Задача  о  нахождении  кратчайшего  пути  в  наше  время  является  очень  актуальной  и  находит  широкое  применение.  Например,  в  туризме,  являющимся  важной  отраслью  экономики  для  любого  города,  страны  —  он  приносит  значительную  долю  дохода.  Туристы  тратят  деньги  на  проживание,  покупку  сувениров,  питание  и  многое  другое.  И,  конечно  же,  на  экскурсии,  поэтому  сейчас  во  многих  городах  туризм  активно  развивается.  Создаются  удобства:  гостиницы,  рестораны,  кафе,  и,  конечно  же,  создаются  сами  туристические  маршруты.  Их  необходимо  создавать  с  учетом  занимаемого  времени,  охватываемых  достопримечательностей,  длины.  Ведь  вряд  ли  найдется  человек,  которому  понравится,  если  его  будут  несколько  часов  водить  по  городу  с  экскурсией,  которая  при  более  рациональной  организации  заняла  бы  минут  сорок.  В  связи  с  этим,  конечно  же,  проложенный  маршрут  должен  быть,  прежде  всего,  кратчайшим.  Таким  образом,  возникает  задача  —  как  обойти  выбранные  достопримечательности  города  по  кратчайшему  маршруту  и  вернуться  в  отправную  точку?  Такая  задача,  по  сути,  является  задачей  коммивояжера,  для  решения  которой  нами  используется  теория  графов.  Все  исследования  и  расчеты  проведены  в  работе  для  города  Самара.

Цель:  построить  оптимальный  туристический  маршрут  по  достопримечательностям  г.  Самара  с  помощью  задачи  коммивояжера  с  использованием  программных  средств.

Задачи:  изучить  методы  и  алгоритмы  решения  задачи  коммивояжера,  использовать  выбранный  алгоритм  для  нахождения  оптимального  маршрута

Результат  исследования:  построенный  кратчайший  туристический  маршрут. 

Основные  понятия

Теория  графов  —  раздел  дискретной  математики,  изучающий  свойства  графов.  В  общем  смысле  граф  представляется  как  множество  вершин  (узлов),  соединённых  рёбрами.

Пусть    —  непустое  конечное  множество,  элементы  этого  множества  будем  называть  вершинами.  Пусть    —  множество  всевозможных  пар  различных  элементов  множества  :    Неориентированным  графом  (графом)    называется  пара    где    —  множество  вершин,    —  множество  ребер,  Обычно  граф  изображают  в  виде  диаграммы,  на  которой  вершины  обозначаются  точками,  а  ребра,  соединяющие  две  вершины  —  линиями  между  этими  точками.  Если    —  ребро,  тогда  вершины  х  и  у  называются  концами  (вершинами)  ребра    [1,  с.  4].

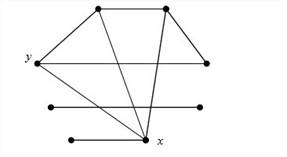
Рисунок  1.  Неориентированный  граф

Матрица  смежности  —  квадратная  матрица,  порядка    на  ,  где    —  количество  вершин  графа,  такая  что    и 

Для  неориентированного  графа  матрица  смежности  всегда  симметрична.

Граф,  каждому  ребру  которого  сопоставлено  число  назовем  взвешенным.  Простой  взвешенный  граф  можно  представить  своей  матрицей  весов  W=[w_ij],где  w_ij  —  вес  соединяющего  вершины  i,  j.  Веса  несуществующих  рёбер  полагают  равными  0  или  ¥.  Матрица  весов,  таким  образом,  будет  являться  простым  обобщением  матрицы  смежности.

Задача  коммивояжёра   —  задача  комбинаторной  оптимизации,  заключающаяся  в  отыскании  самого  выгодного  маршрута,  проходящего  через  указанные  вершины  по  одному  разу  с  последующим  возвратом  в  исходную  вершину.

За  оптимальный  путь  возьмем  кратчайший  путь  по  длине.

Алгоритмы  решения  задачи  коммивояжера

Существует  множество  алгоритмов  решения  задачи  коммивояжера:  полный  перебор,  случайный  перебор,  жадный  алгоритм,  метод  ветвей  и  границ,  муравьиный  алгоритм,  генетический  алгоритм  и  другие.

Общепризнанно,  что  задача  коммивояжера  в  общем  случае  точно  решается  только  полным  перебором  всех  вариантов,  так  как  с  ростом  количества  узлов  время,  затрачиваемое  на  полный  перебор,  растет  экспоненциально.  Например,  на  машине  с  четырехъядерным  процессором  (2,67  ГГц)  задача  в  10  узлов  рассчитывается  в  среднем  за  5  мс.,  в  20  узлов  —  за  15  мин.,  а  на  расчет  оптимального  пути  для  60  узлов  уйдет  более  6  триллионов  лет  [2].  Поэтому  для  сокращения  времени  вычисления  при  большом  количестве  узлов  используют  эвристические  методы,  с  помощью  которых  находится  приближенное  решение  задачи.

Жадный  алгоритм

Жадный  алгоритм  имитирует  поведение  жадного  человека:  выбирается  самое  короткое,  еще  не  выбранное  ребро  так,  чтобы  оно  не  образовывало  цикл  с  уже  выбранными  ребрами,  но,  как  правило,  на  последних  шагах  приходится  жестко  расплачиваться  за  «жадность».  Использование  такого  алгоритма  при  решении  задачи  коммивояжера  приводит  к  выбору  ближайшей,  ранее  не  посещенной  вершины.

Жадный  алгоритм  чаще  всего  не  даёт  оптимального  решения  при  решении  задачи  коммивояжера.

Муравьиный  алгоритм

В  настоящее  время  одним  из  лучших  эвристических  алгоритмов  является  муравьиный.  Он  относится  к  так  называемым  «природным  вычислениям»  —  это  интенсивно  разрабатываемое  направление,  объединяющее  математические  методы,  основанные  на  принципе  природных  механизмов  принятия  решений.  Кроме  муравьиного  алгоритма,  основанного  на  поведении  колонии  муравьев,  примерами  таких  методов  является  алгоритм,  имитирующие  поведение  роя  пчёл.  Существует  ещё  несколько  алгоритмов,  но  они  малоизвестны.  Имитация  самоорганизации  муравьиной  колонии  составляет  основу  муравьиных  алгоритмов  оптимизации.  Колония  муравьев  рассматривается  как  многоагентная  система,  где  каждый  агент  (муравей)  функционирует  отдельно  по  примитивным  правилам,  но  поведение  всей  системы  получается  разумным.  Основой  поведения  муравьиной  колонии  является  самоорганизация.  Она  обеспечивает  достижение  общих  целей  колонии  на  основе  низкоуровневого  взаимодействия.  Особенностями  колонии  является  наличие  непрямого  обмена,  который  и  используется  в  муравьиных  алгоритмах.  Таким  образом,  в  общем  случае  рассматриваются  слепые  муравьи,  не  способные  чувствовать  близость  пищи.

Основой  поведения  муравьиной  колонии  является  самоорганизация,  которая  обеспечивает  достижение  общих  целей  колонии  на  основе  низкоуровневого  взаимодействия.  Установлено,  что  такое  взаимодействие  осуществляется  через  секрет  специальных  желез,  откладываемый  муравьями  при  их  перемещении  —  феромон.  Его  концентрация  на  пути  и  определяет  предпочтительность  движения.  Адаптивность  поведения  реализуется  испарением  феромона,  который  в  природе  воспринимается  муравьями  втечение  нескольких  суток.  Передвигаясь  по  некоторому  пути,  муравей  оставляет  след  из  феромона,  который  дает  другим  муравьям  информацию,  позволяющую  выбрать  наилучший  путь.  Благодаря  этому,  муравьи  способны  быстро  находить  новый  путь,  если  старый,  по  каким-либо  причинам,  оказался  недоступен.  Моделирование  поведения  муравьев,  связанного  с  этой  способностью,  является  идеей  муравьиного  алгоритма  [3].

При  решении  задачи  коммивояжера  муравьиный  алгоритм  также  приобретает  некоторые  особенности:

Муравьи  имеют  собственную  «память».  Поскольку  каждая  достопримечательность  может  быть  посещена  только  один  раз,  то  у  каждого  муравья  есть  список  уже  посещённых  достопримечательностей  —  список  запретов.  Обозначим  через    список  городов,  которые  необходимо  посетить  муравью  k,  находящемуся  в  городе  i. 

Муравьи  обладают  «зрением»  –  видимость  есть  эвристическое  желание  посетить  достопримечательность  j,  если  муравей  находится  у  достопримечательности  i.  Будем  считать,  что  видимость  обратно  пропорциональна  расстоянию  между  достопримечательностями  .

Муравьи  обладают  «обонянием»  —  они  могут  улавливать  след  феромона,  подтверждающий  желание  посетить  достопримечательность  j  после  достопримечательности  i  на  основании  опыта  других  муравьёв.

Количество  феромона  на  ребре    в  момент  времени  t  обозначим  через

Тогда  учетом  особенностей  задачи  коммивояжера  алгоритм  представим  в  следующем  виде  [4,  с.  8]: 

1.  Создание  муравьев

Общее  количество  муравьев  равно  количеству  достопримечательностей.

Каждый  муравей  начинает  маршрут  от  «своей»  достопримечательности.

Начальный  уровень  феромона  —  небольшое  положительное  число,  поскольку  вероятности  перехода  в  следующую  вершину  на  начальном  шаге  не  должны  быть  нулевыми. 

2.  Поиск  решения

Вероятностно-пропорциональное  правило,  определяющее  вероятность  перехода  k-го  муравья  из  достопримечательности  i  в  j:

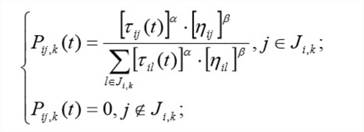(1)

где:    —  уровень  феромона,

  —  эвристическое  расстояние,  а 

—  константные  параметры,  задающие  веса  следа  феромона.  При  α  =  0  алгоритм  вырождается  в  жадный.  При  β  =  0  выбор  происходит  только  на  основании  феромона,  что  приводит  к  субоптимальным  решениям.  Поэтому  необходим  компромисс  между  этими  величинами,  который  находится  экспериментально.

Замечание:  выбор  достопримечательности  является  вероятностным,  правило  (1)  лишь  определяет  ширину  зоны  достопримечательности  j,  оно  не  изменяется  в  ходе  алгоритма,  но  для  разных  муравьев  будет  отличаться,  так  как  они  будут  иметь  разные  списки  разрешенных  достопримечательностей.

В  общую  зону  всех  достопримечательностей  ,  бросается  случайное  число,  которое  и  определяет  выбор  муравья.

3.  Обновление  феромона

Пройдя  ребро,  муравей  откладывает  на  нём  некоторое  количество  феромона,  которое  должно  быть  связано  с  оптимальностью  сделанного  выбора.  Пусть    есть  маршрут,  пройденный  муравьём  k  к  моменту  времени  t,    —  длина  этого  маршрута,  а  Q  —  параметр,  имеющий  значение  порядка  длины  оптимального  пути,  то  есть    —  феромон,  откладываемый  k-ым  муравьем,  использующим  ребро  .  Тогда  откладываемое  количество  феромона  может  быть  задано  в  виде:

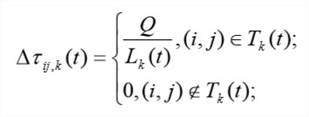(2)

Правила  внешней  среды  определяют,  в  первую  очередь,  испарение  феромона.  Пусть  есть  коэффициент  испарения,  тогда  правило  испарения  имеет  вид:

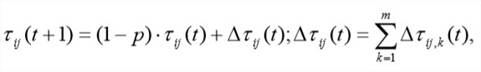  (3)

где  —  количество  муравьёв  в  колонии.

4.  Дополнительные  действия

Дополнительная  модификация  алгоритма  может  состоять  во  введении  «элитных»  муравьёв,  усиливающих  рёбра  наилучшего  маршрута,  найденного  с  начала  работы  алгоритма.

Построение  оптимального  туристического  маршрута

На  рис.  2.  представлена  карта  г.  Самара  с  отмеченными  достопримечательностями,  которые  были  выбраны  по  результатам  опроса  жителей  г.  Самара  и  являются,  по  их  мнению,  наиболее  интересными  для  посещения  туриста  местами.

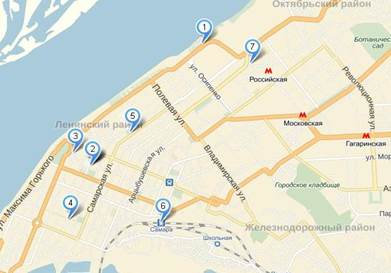
Рисунок  2.  Достопримечательности  города  Самара

1.  Скульптурная  композиция  «Ладья»

2.  Самарский  академический  театр  оперы  и  балета

3.  Самарский  академический  театр  драмы  им.  М.  Горького

4.  Ленинградская  улица

5.  Самарская  площадь

6.  Железнодорожный  вокзал

7.  Музейно-выставочный  комплекс  «Самара  космическая»

Для  нахождения  оптимального  маршрута  с  возвратом  в  исходную  точку  был  выбран  муравьиный  алгоритм,  дающий  эвристическое  решение.  Пунктом  отправления  является  железнодорожный  вокзал.

Для  наглядности,  зададим  матрицу  весов  графа  (табл.1.),  где  вершинами  1—6  являются  достопримечательности,  а  расстояния  (содержимое  таблицы)  указаны  в  километрах:

Таблица  1. 

Матрица  весов

Расстояния  между  пунктами  были  вычислены  при  помощи  сервиса  интернет  .

Для  решения  нашей  задачи  возьмем  следующие  начальные  условия:

где    —  ребро,  соединяющее  вершины  i  и  j;    —  эвристическое  расстояние  между  вершинами  i  и  j;    —  концентрация  ферамона  на  ребре  .

Таблица  2. 

Начальные  условия

С  помощью  программного  обеспечения,  написанного  нами  на  языке  программирования  С++,  было  рассчитано,  что  наилучшим  является  маршрут:

6–>4–>3–>2–>5–>1–>7–>6.

Его  длина  составляет  15,1  км.

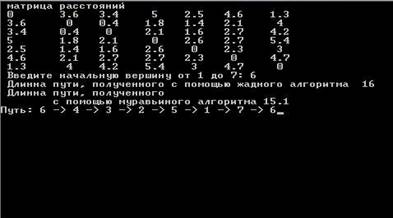
Рисунок  3.  Пример  работы  программы

Заключение

Теория  графов  позволяет  решать  задачи,  встречающиеся  в  повседневной  жизни  постоянно,  одна  из  таких  задач  была  рассмотрена  нами  —  это  нахождение  кратчайшего  маршрута,  полученное  решение  может  быть  применимо  к  любым  объектам,  между  которыми  необходимо  составить  маршрут  с  возвращением  в  исходную  точку.  При  этом  по  результатам,  полученным  с  помощью  программы  видно,  что  выбранный  алгоритм  дает  лучший  результат  по  сравнению,  например,  с  жадным  алгоритмом.

Список  литературы:

1.Додонова  Н.Л.  Конспект  лекций  по  дисциплине  теория  конечных  графов  и  ее  применения  Самара:  2010  —  с.  52 

2.Применение  муравьиных  алгоритмов  при  решении  задач  оптимизации   [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://works.doklad.ru/view/BsaT-3tALgc.html  (дата  обращения  15.04.2015).

3.Решение  задачи  коммивояжёра  рекурсивным  полным  перебором  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://habrahabr.ru/post/151151/  (дата  обращения  15.04.2015).

4.Чураков  М.,  Якушев  А.  Муравьиные  алгоритмы  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://rain.ifmo.ru/cat/data/theory/unsorted/ant-algo-2006/article.pdf  (дата  обращения  15.04.2015).