ДИФФЕРЕНЦИАЛЬНЫЕ  УРАВНЕНИЯ  В  НЕФТЕГАЗОВОМ  ДЕЛЕ

Алтынбаев  Айдар  Рафисович

студент  1-го  курса  Филиал  ФГБОУ  ВПО  «Уфимский  государственный  нефтяной  технический  университет»  в  г.  Октябрьском,  РФ,  г.  Октябрьск

E -mail:  aidar.altunbaev@gmail.com

Идиятуллин  Альберт  Фанисович

студент  1-го  курса  Филиал  ФГБОУ  ВПО  «Уфимский  государственный  нефтяной  технический  университет»  в  г.  Октябрьском,  РФ,  г.  Октябрьск

E -mail:  albert119955@mail.ru

Габдрахманова  Клара  Фаткулиновна

научный  руководитель,  канд.  пед.  наук,  доцент,  филиал  ФГБОУ  ВПО  «Уфимский  государственный  нефтяной  технический  университет»  в  г.  Октябрьском,  РФ,  г.  Октябрьск

В  данной  статье  мы  рассмотрим  некоторые  дифференциальные  уравнения  математической  физики,  а  также  обозначим  их  роль  в  нефтегазовом  деле.

Большинство  физических  процессов,  изучаемые  в  теории  упругости,  гидродинамике,  электродинамике,  теории  надежности  применяемых  инструментов  и  т.  д.,  образуют  круг  вопросов  математической  физики.  Задачи  математической  физики  приводят  к  дифференциальным  уравнениям  в  частных  производных.

Дифференциальное  уравнение  в  частных  производных  —  это  уравнение,  в  котором  искомая  функция  от  многих  переменных  находится  под  знаком  производной.

Порядок  старшей  производной  искомой  функции,  входящей  в  дифференциальное  уравнение,  определяет  порядок  заданного  уравнения.

Решение  дифференциальных  уравнений  в  частных  производных  представляет  определенные  трудности,  в  общем  виде  разрешима  малая  часть  таких  уравнений.

Уравнение  колебания  струны

Прежде  было  зафиксировано,  что  дифференциальное  уравнение  в  частных  производных  гиперболического  типа    именуется  волновым  уравнением.  Это  уравнение  изображает  процесс  распространения  возмущений  в  некоторой  среде,  в  частности,  малые  поперечные  колебания  тонкой  струны,  колебательные  процессы  в  сплошных  средах  и  в  электродинамике.  Для  описания  среды  ее  физические  характеристики  определяют  заданием  некой  величины  (или  величин).  Изменение  данных  величин  с  течением  времени  именуют  движением.

Под  струной  понимают  тонкую  нить,  которая  работает  на  растяжение,  но  не  на  изгиб.  При  растяжении  ненатянутой  струны  в  ней  возникает  напряжение.  

  (1)

Уравнение  (1)  называется  уравнением  колебаний  струны  или  одномерным  волновым  уравнением.  Это  одно  из  простейших  и  в  то  же  время  главнейших  дифференциальных  уравнений  математической  физики.  Как  мы  позже  заметим,  к  нему  сводится  не  только  анализируемая  задача,  но  и  многие  другие.

Если  g(x,t)≡0,  то  уравнение  (1)  называется  однородным;  оно  описывает  свободные  колебания  струны  без  влияния  внешних  сил.

Если  g(x,t)  не  равно  нулю,  то  уравнение  называется  неоднородным,  в  этом  случае  рассматриваются  вынужденные  колебания  струны.  Когда  на  струну  действуют  только  сила  тяжести,  а  натяжение  струны  Т₀  велико,  мы  можем  пренебречь  вторым  слагаемым  в  правой  части  уравнения  струны  по  сравнению  с  первым  и  рассматривать,  поэтому,  колебания  струны  как  свободные.

Вывод  уравнения  колебаний  струны  (1)  проходит  целым  рядом  допущений  как  механического,  так  и  геометрического  порядков.  Такое  же  положение,  конечно,  присутствует  и  при  выводе  дифференциальных  уравнений  (как  в  частных  производных,  так  и  обыкновенных)  иных  задач  математической  физики.  Вопрос  о  том,  насколько  точно  уравнение  изображает  физический  процесс,  может  быть  прорешён  только  сравнением  результатов,  полученных  при  прорешивании  уравнения  экспериментальным  путем.

Уравнение  теплопроводности

Уравнение  теплопроводности   —  значимое  уравнение  в  частных  производных,  которое  изображает  распространение  тепла  в  данной  области  пространства  во  времени.

Для  функции  u(x,y,z,t)  трёх  пространственных  переменных  (x,y,z)  и  времени  t,  уравнение  теплопроводности  обладает  видом:

,

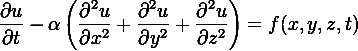где    —  функция  тепловых  источников.

Уравнение  колебания  мембраны

Мембраной  или  перепонкой  именуется  диафрагма,  натянутая  на  плоский  контур,  которая,  подобно  струне,  не  сопротивляется  струне  и  сдвигу.  Если  ввести  в  плоскости  этого  контура  оси  Ох  и  Оу  декартовой  системы  координат,  то  при  малых  поперечных  колебаниях  точка  мембраны,  имевшая  в  положении  равновесия  координаты  (х,  у,  0),  будет  иметь  координаты  (х,  у,  u),  причем  u  можно  полагать  однозначной  функцией  х,  у  и  времени  t.  Эта  функция  удовлетворяет  уравнению  колебаний  мембраны:

    [3]

где:  ρ  —  плотность,

Т  —  натяжение  диафрагмы.

Уравнение  (2)  отличается  от  уравнения  колебаний  струны  только  тем,  что  вторая  производная  по  Х,  заменена  здесь  лапласианом

Хорошо  знакома  роль  моделей  при  исследовании  разнообразных  вопросов  техники.  К  примеру,  гидротехники  при  проектировании  плотины  часто  создают  в  существенно  меньшем  размере  ее  модель,  чтобы,  проводя  опыты  над  ней  в  лабораториях,  сделать  некие  выводы  о  характере  усилий,  влияющих  на  настоящую  плотину.  Такую  же  роль  играют  модели  проектируемых  мостов,  крыльев  и  фюзеляжа  самолетов  и  др.  Разумеется,  данные,  полученные  при  исследовании  моделей,  нельзя  просто  переносить  на  реальные  объекты.  Ведь  в  лаборатории  нельзя  создать  все  условия,  которые  могут  встретиться  в  действительности,  да  и,  кроме  того,  явления,  происходящие  при  исследовании  модели,  далеко  не  всегда  в  точности  копируют  соответствующие  явления  в  природе.  Тем  не  менее,  наиболее  значимые  черты  процесса  все-таки  часто  удается  улавливать,  и  дальнейшая  задача  проектировщика  в  том  и  заключается,  чтобы  увязать  наблюденные  на  модели  факты  с  теми,  которые  столкнутся  в  натуре.

Подобную  же  роль  в  физике  играет  и  исследование  дифференциальных  уравнений  математической  физики.  Учитывая  ключевые  закономерности  физического  процесса,  мы  формируем  его  математическую  модель.  Исследование  этой  модели  и  дает  возможность  делать  установленные  суждения  о  характере  процесса.

Заключение:   дифференциальные  уравнения  математической  физики  широко  используются  в  нефтегазовом  деле.  Например,  при  описании  рефлекторных  возмущениях  пласта  при  механических  действиях  на  него  (например,  буром),  используется  уравнение  колебания  мембраны.  Под  мембраной  здесь  подразумевается  пласт;  а  при  описании  движении  колонны  насосных  штанг  или  бурильной  колонны  используется  уравнение  колебания  струны.  Точное  решение  задач  динамики  спуска  и  подъема  бурильной  колонны  сводится  к  вычислению  огромных  рядов,  что  усложняет  их  применение  в  инженерных  расчетах.  В  научных  исследованиях  по  данному  вопросу  эти  задачи  приводятся  к  изучению  движения  приведенных  масс,  связанных  между  собой  упругими  элементами.

Для  составления  дифференциального  уравнения  движения  элементов  системы  спуска,  опуская  ряд  менее  существенных,  второстепенных  факторов,  выделяют  наиболее  существенные,  составляя  упрощенную  схему  подъемной  конструкции.

Список  литературы:

1.Алимов  Б.А.,  Арипджонов  М.К.  Конспект  лекций  по  курсу  Методология  научного  творчества.

2.Гуторов  Ю.А.,  Габдрахманова  К.Ф.,  Ларин  П.  А.  Теория  вероятностей  и  математическая  статистика  в  примерах  и  задачах  по  разработке  нефтяных  месторождений.  Уфа:  Изд-во  УГНТУ.  2013,  —  120  с.

3.Габдрахманова  К.Ф.,  Усманова  Ф.К.  Прикладные  методы  решения  задач  в  нефтегазовом  деле.  Часть  I.  Уфа:  Изд-во  УГНТУ.  2012,  —  197  с.