К  ВОПРОСУ  О  СОГЛАСОВАННОСТИ  МОРСКОЙ  И  МАТЕМАТИЧЕСКОЙ  ТЕРМИНОЛОГИИ

Штепа  Александр  Александрович

студент  1  курса,  кафедра  судовождения  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет»,  РФ,  г.  Керчь

E -mail:  special_for_uplay@mail.ru

Чернобай  Кирилл  Сергеевич

студент  1  курса,  кафедра  судовождения  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет»,  РФ,  г.  Керчь

E -mail:  Kirilus9@gmail.com

Егорова  Светлана  Николаевна

научный  руководитель,  кафедра  высшей  математики  и  физики  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет»,  РФ,  г.  Керчь

В  настоящее  время  идет  становление  новой  системы  образования,  ориентированной  на  динамичные  изменения  в  жизни  всего  мирового  сообщества.  Формирование  профессиональных  качеств  будущих  специалистов  рассматривается  как  комплексный  процесс  приобретения  ключевых,  общепрофессиональных  и  специальных  компетенций,  определяющих  способность  специалиста  отвечать  требованиям  будущей  профессии.  С  позиций  этого  подхода  математическая  подготовка  будущих  судоводителей  может  рассматриваться  как  реализация  предметной  компетенции,  отличительной  особенностью  которой  должна  стать  профессиональная  направленность.

Целью  данной  статьи  является  изучение  вопроса  согласованности  математической  и  морской  терминологии  и  определение  его  роли  в  формировании  математической  компетенции  будущих  судоводителей. 

Математический  язык  является  универсальным.  Его  терминология  используется  в  базовых  инженерных  дисциплинах,  не  вызывая  у  студентов  серьезных  сложностей  восприятия.  Таковые  могут  возникнуть  при  изучении  специальных  дисциплин,  в  связи  с  исторически  сложившимся  несоответствием  терминологии.  Например,  при  сравнении  понятий  курсов  математики  и  профильных  для  судоводителей  дисциплин,  можно  выделить  ряд  терминов,  обозначающих  по  сути  одинаковые  понятия,  но  по  своему  выражению  заметно  различающихся.

В  отдельности  морская  и  математическая  терминологии  были  объектами  изучения  многих  исследователей.  Так,  Ш.Ч.  Миттала  [5]  рассматривает  проблему  определения  математического  термина;  Р.В.  Гарифуллина  [1]  исследует  тему  математической  терминологии  в  русском  языке;  А.А.  Петрова  [7]  и  М.В.  Попова  [10]  устанавливают  связь  морской  терминологии  с  английским  и  немецким  языками.  Вопрос  согласованности  математических  и  морских  терминов  в  процессе  подготовки  будущих  судоводителей  практически  не  рассматривался.  В  отдельных  работах  [2]  приведены  частные  случаи  согласованности  этих  терминов. 

Недостаточная  разработанность  данной  темы  и  определила  задачи  нашего  исследования. 

В  своей  работе  мы  рассмотрели  ряд  современных  учебников  по  дисциплинам  «Основы  судовождения»  и  «Математика»  [3;  4;  6;  8;  9].  Наиболее  важными  понятиями,  на  наш  взгляд,  из  курса  математики  для  судоводителей  можно  выделить  следующие:  вектор,  начало  и  конец  вектора,  геометрические  правила  сложения  и  вычитания  векторов;  кривые  и  поверхности  2-го  порядка;  функция  нескольких  переменных  и  связанные  с  ней  понятия  изолинии  и  градиента.  Рассмотрим  подробнее,  как  эти  понятия  связаны  с  терминами  судовождения.

В  практике  судовождения  векторная  алгебра  служит  основой  графического  счисления  пути  судна.  Все  построения  на  меркаторской  карте  осуществляются  по  координатам  вектора,  причем  начало  вектора  трактуется  как  точка  отшествия,  а  конец  –  как  точка  пришествия.  Координаты  точек  задаются  указанием  их  широты  и  долготы.  При  прокладке  пути  судна  на  карте  судоводителю  приходится  учитывать  влияние  течений  и  дрейфа.  В  этом  случае  графические  построения  сводятся  к  определению  направления  и  величины  абсолютной  скорости  судна  по  его  относительной  скорости  и  элементам  течения  или  дрейфа,  другими  словами,  строится,  так  называемый,  скоростной  (путевой)  треугольник  (рис.  1).  К  сожалению,  редко  у  кого  из  студентов  третьего  курса  возникает  аналогия  с  построением  геометрической  суммы  векторов  по  правилу  треугольника  или  параллелограмма.

Рисунок  1.  Путевой  треугольник

При  решении  задач  геодезии,  навигации  и  картографии  возникает  необходимость  согласования  морских  терминов  с  темой  «Кривые  и  поверхности  2-го  порядка».  Так,  кривые  второго  порядка  можно  обнаружить  в  схеме  работы  РЛС.  В  данном  случае  гипербола  соответствует  разности  расстояния  между  двумя  береговыми  станциями.  Точка  пересечения  двух  гипербол  будет  являться  обсервованным  местом  судна.

Важное  место  в  подготовке  судоводителя  занимает  изучение  теории  погрешностей.  Особенно  важно  уметь  производить  оценку  точности  обсервованного  места  судна,  т.  е.  устанавливать  границы  той  области,  в  пределах  которой  с  заданной  вероятностью  может  находиться  истинное  место  судна  [3,  с.  148].  При  нормальном  распределении  погрешностей  измерения  такая  площадь  ограничена  эллипсом,  который  называют  эллиптической  погрешностью.  Эллиптическая  погрешность  в  общем  случае  вычисляется  с  помощью  ЭВМ  и  используется  при  предварительном  расчете  навигационной  безопасности  плавания  в  узкости,  по  фарватеру  и  вблизи  навигационных  опасностей.  Относительно  обсервованной  точки  можно  провести  бесчисленное  множество  подобных  эллипсов,  каждый  из  которых  соответствует  определенной  вероятности  нахождения  действительного  места  в  его  пределах.  Эллипс  погрешностей  характеризуется  тремя  элементами:  большой  главной  полуосью  а,  малой  главной  полуосью  b  и  углом  α,  под  которым  большая  ось  пересекается  с  меридианом  (рис.  2).

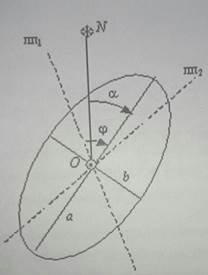
Рисунок  2.  Эллипс  погрешностей

Более  простой  характеристикой  погрешности  является  площадь,  ограниченная  кругом,  называемым  радиальной  погрешностью.  Радиус  этого  круга  определенным  образом  сопряжен  с  эллипсом  погрешностей.

Поверхности  2-го  порядка  изучаются  судоводителями  довольно  поверхностно,  студенты  не  придают  особого  смысла  параметрам  эллипсоида,  сферы,  входящим  в  их  уравнения.  Параметры  эллипсоида  Красовского,  принятого  в  судовождении  для  расчетов  пути  судна  по  поверхности  Земли,  могут  служить  хорошим  примером  придания  смысла  значениям  полуосей  эллипсоида.  В  некоторых  морских  расчетах,  например,  в  задачах  мореходной  астрономии,  Земля  принимается  за  сферу.

Понятия  изолинии  и  градиента  также  являются  важными  для  судоводителей  —  они  необходимы  для  чтения  карт  глубин,  давления,  течений  и  самое  главное  —  для  определения  места  судна.  Само  понятие  звучит  так:  «Изолинией  называется  линия,  отвечающая  постоянному  значению  некоторой  геометрической  величины,  являющейся  функцией  от  координат  наблюдателя,  т.  е.  геометрическим  местом  точек,  в  которых  эта  величина  имеет  постоянное  значение»  [6,  с.  65].  В  судовождении  используется  термин  «навигационная  изолиния»,  который  обозначает  геометрическое  место  точек  равных  значений  навигационных  параметров.  Уравнение  навигационной  изолинии  —  это  ни  что  иное  как  уравнение,  составленное  для  функции  нескольких  переменных  (в  данном  случае  λ-долготы  и  φ-широты):  U₀  =  f  (  λ,  φ  )=  const.

Важнейшей  характеристикой  навигационной  функции  является  ее  вектор-градиент,  который  показывает  максимальную  скорость  изменения  навигационной  функции  (максимальную  скорость  изменения  навигационного  параметра).  Для  нахождения  этой  скорости,  т.  е.  модуля  вектора-градиента,  необходимо  вычислять  частные  производные  от  навигационной  функции.

Целый  раздел  в  навигации,  связанный  с  определением  места  судна,  строится  на  понятии  линии  положения.  Математическое  соответствие  этому  термину  определяет  касательную  к  изолинии.  Для  её  построения  необходимо  использовать  свойство  перпендикулярности  к  вектору-градиенту,  а  аналитический  способ  задания  предполагает  использование  уравнения  прямой  на  плоскости.

Исходя  из  изложенных  выше  соображений,  можно  рекомендовать  будущим  судоводителям  в  процессе  изучения  математики  совмещать  вводимые  понятия  классической  математики  с  использованием  похожей  терминологии  по  специальности.  Проводить  такие  методические  параллели  необходимо  уже  в  начале  обучения,  т.  к.  подобные  приемы  на  старших  курсах,  когда  начинается  углубленное  изучение  спецпредметов  и  меняется  настрой  и  мотивация  студентов,  могут  быть  запоздалыми.  Также  полезно  введение  интегрированных  курсов  по  математике  и  профильным  дисциплинам  с  использованием  инновационных  технологий  обучения.  В  качестве  перспектив  развития  нашей  темы  видим  участие  в  разработке  подобных  инициатив.

Список  литературы:

1.Гарифуллина  Р.В.  Физико-математическая  терминология  в  русском  языке:  лексико-семантический,  словообразовательный  и  функциональный  аспекты:  Дис…канд.  фил.  наук  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.dissercat.com/content/fiziko-matematicheskaya-terminologiya-v-russkom-yazyke-leksiko-semanticheskii-slovoobrazovat   (дата  обращения:  20.12.2014).

2.Егорова  С.Н.  О  согласованности  математической  и  морской  терминологии  как  элементе  профессиональной  направленности  курса  высшей  математики  для  будущих  судоводителей  //  Современные  достижения  в  науке  и  образовании:  сб.  тр.  V  Междунар.  науч.  конф.,  27  сентяб.—4  октяб.  2011  г.,  г.  Нетания  (Израиль):  в  2  т.  Хмельницкий  :  ХНУ,  —  2011.  —  Т.  2.  —  С.  76—79.

3.Кожухов  В.П.,  Григорьев  В.В.,  Лукин  С.М.  Математические  основы  судовождения:  учеб.  для  вузов  мор.  трансп.  М.:  Транспорт,  1987.  —  208  с. 

4.Макаров  И.В.  Морское  дело:  учебник  для  мореход.  училищ.  М.:  Транспорт,  1989.  —  287  с.

5.Миттала  Ш.Ч.  Русская  математическая  терминология:  Дис  .…  канд.  фил.  наук  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.dissercat.com/content/russkaya-matematicheskaya-terminologiya  (дата  обращения:  20.12.2014).

6.Основы  морского  судовождения:  учебник  для  вузов  /  Фатьянов  Р.Н.,  Семенов  Ю.К.,  Костюков  Б.Н.,  Милославская  Е.П.  2-е  изд.,  перераб.  и  доп.  М.:  Транспорт,  1985.  —  344  с.

7.Петрова  А.А.  Метаязыковая  аспектность  модальных  отношений  в  процессе  перевода:  На  материале  морской  терминологии  русского  и  английского  языков:  Дис…канд.  фил.  наук  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.dissercat.com/content/metayazykovaya-aspektnost-modalnykh-otnoshenii-v-protsesse-perevoda-na-materiale-morskoi-ter#ixzz3Q0toklrT   (дата  обращения:  20.12.2014).

8.Пискунов  Н.С.  Дифференциальное  и  интегральное  исчисления  для  втузов:  учебное  пособие  для  втузов.  Т.  1.  М.:  Наука,  1985.  —  432  с.

9.Письменный  Д.Т.  Конспект  лекций  по  высшей  математике:  полный  курс.  М.:  Айрис-Пресс,  2009.  —  608  с.:  ил. 

10.Попова  М.В.  Германские  заимствования  в  русской  мореходной  терминологии:  Дис…канд.  фил.  наук  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.dissercat.com/content/germanskie-zaimstvovaniya-v-russkoi-morekhodnoi-terminologii   (дата  обращения:  20.12.2014).