СРАВНИТЕЛЬНЫЙ  АНАЛИЗ  ПРЯМЫХ  МЕТОДОВ  МИНИМИЗАЦИИ  ФУНКЦИИ  ОДНОЙ  ПЕРЕМЕННОЙ

Тюбина  Ольга  Игоревна

студент  2  курса,  экономический  факультет,  НОУ  ВПО  «Университет  управления  «ТИСБИ»,  г.  Казань

E-mail: 

,

Пантелеева  Лейсан  Ренатовна

научный  руководитель,  канд.  техн.  наук,  кафедра  математики,  НОУ  ВПО  «Университет  управления  «ТИСБИ»,  г.  Казань

В  любой  сфере  человеческой  деятельности  мы  встречаемся  с  оптимизацией.  Экономическое  планирование,  управление,  проектирование  сложных  объектов  всегда  направлено  на  поиск  наилучшего  варианта  с  точки  зрения  намеченной  цели.

Многие  задачи  оптимизации  сводятся  к  отысканию  наименьшего  или  наибольшего  значения  некоторой  функции,  которую  принято  называть  целевой  функцией.  Методы  решения  таких  задач  существенно  зависят  от  свойств  целевой  функции.

Методы,  использующие  только  значения  функции  и  не  требующие  вычисления  ее  производных,  принято  называть  прямыми  методами  минимизации.  Большим  достоинством  прямых  методов  является  то,  что  от  целевой  функции  не  требуется  дифференцируемости.  Более  того,  она  может  быть  не  задана  в  аналитическом  виде.  Единственное,  на  чем  основаны  алгоритмы  прямых  методов  минимизации,  это  возможность  определения  значений  функции  в  заданных  точках.

Рассмотрим  наиболее  распространенные  прямые  методы  решения  задачи  минимизации  функции  одной  переменной,  заданной  на  отрезке:

К  ним  относятся  методы  перебора,  дихотомии,  золотого  сечения  и  Фибоначчи. 

Самым  слабым  требованием  на  функцию  f(x),  позволяющим  использовать  прямые  методы,  является  ее  унимодальность  или  строгая  квазивыпуклость.  Поэтому  будем  считать  функцию  f(x)  строго  квазивыпуклой  на  заданном  отрезке,  т.  е.  имеющей  на  [a,  b]  единственный  минимум  X_*,  который  является  глобальным  минимумом.

Существуют  работы,  например  [1—3],  в  которых  приводится  сравнительный  анализ  эффективности  прямых  методов  поиска  минимума.  При  этом  либо  не  все  критерии  сравнения  подробно  рассматриваются,  либо  не  все  перечисленные  выше  методы  участвуют  в  сравнении.

В  данной  работе  изложим  основные  идеи  рассматриваемых  методов,  приведем  формулы,  на  основании  которых  осуществим  подробный  сравнительный  анализ  методов. 

Простейшим  из  прямых  методов  является  метод  перебора.  Он  заключается  в  последовательном  переборе  всех  значений  точек,  делящих  отрезок  [a,  b]  на  n  равных  частей,  с  вычислением  значений  целевой  функции  в  каждой  точке.  Путем  выбора  наименьшего  из  всех  вычисленных  значений  функции  и  находится  решение  задачи.

Погрешность  определения  точки  минимума  функции  f(x)  методом  перебора  не  превосходит  величины    Чтобы  обеспечить  требуемую  точность  ε  определения  точки  х_*,  число  отрезков  разбиения  n  необходимо  выбрать  из  условия:

Если  при  реализации  метода  перебора  потребовалось  вычислить  N  значений  функции  f(x),  то  это  означает,  что  отрезок  [a,  b]  был  разбит  на  n=N-1  частей.  Поэтому  точность  решения  ,  которую  обеспечивает  метод  перебора  в  результате  N  вычислений  f(x),  будет: 

Следующие  методы  —  метод  дихотомии,  метод  золотого  сечения  и  метод  Фибоначчи  —  объединяются  одной  идеей:  на  каждом  шаге  алгоритма  отсекается  отрезок,  включающийся  в  [a,  b],  на  котором  заведомо  нет  точки  X_* - решения  задачи  (1).  Эти  методы  принято  называть  методами  отсечений. 

В  методе  дихотомии  экстремум  локализуется  путем  сравнения  двух  значений  функции  в  точках,  отстоящих  от  середины  отрезка  на    —  параметр  метода.  После  n  итераций  длина  отрезка  поиска  точки  X_*   (отрезка  локализации)  равна    [1—3].

Если  в  качестве  приближенного  значения  X_*   взять  середину  отрезка  локализации,  то  будет  достигнута  точность  определения  точки  минимума: 

Следовательно,  число  n  итераций  метода  дихотомии,  необходимое  для  определения  точки  X_*   с  точностью ε ,  определяется  неравенствами:

При  малом  значении δ   величина 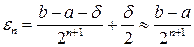 .  На  каждой  итерации  метода  дихотомии  вычисляются  два  значения  .  Поэтому  после  N  вычислений    производится    итераций  и  достигается  точность  определения  X_* :

Из  формул  (4),  (6)  следует,  что  отрезок  локализации  после  N  вычислений    имеет  длину:

Метод  золотого  сечения  основан  на  делении  отрезка  локализации  по  известному  правилу  золотого  сечения.  Это  правило  определяет  такое  симметричное  расположение  пробных  точек  на  текущем  отрезке,  при  котором  одна  из  них  становится  пробной  точкой  на  новом  отрезке,  полученном  после  исключения  части  исходного  отрезка.  Использование  таких  точек  позволяет  на  каждой  итерации  метода  золотого  сечения,  кроме  первой,  ограничиться  определением  только  одного  значения  ,  так  как  другое  значение  уже  найдено  на  одной  из  предыдущих  итераций.

На  каждой  итерации  метода  золотого  сечения  отрезок  локализации  уменьшается  в  одном  и  том  же  отношении    поэтому  в  результате  n  итераций  его  длина  становится    [1-3]. 

Таким  образом,  точность  определения  точки  X_*   после  n  итераций  находится  из  равенства:

а  условием  окончания  поиска  точки  X_*   с  точностью ε   служит  неравенство  .

Число  итераций,  необходимое  для  достижения  заданной  точности  ε,  можно  найти  из  условия    с  учетом  соотношения  (8):

Так  как  N  вычислений    позволяет  выполнить  N-1  итераций  метода  золотого  сечения,  то  достигнутая  в  результате  этого  точность  определения  X_*   составляет:

а  длина  отрезка  локализации  с  учетом  формул  (8),  (10)  будет  равна:

Метод  Фибоначчи  строится  по  схеме  метода  золотого  сечения,  но  расположение  пробных  точек  определяется  с  помощью  чисел  Фибоначчи  F_n,  задаваемых  правилом:

.

Известно,  что  при  достаточно  большом  числе  n  пробные  точки,  определяемые  по  формулам  [2]:

осуществляют  деление  отрезка,  являющееся  близким  к  золотому  сечению.

После  n  итераций  метода  Фибоначчи  длина  отрезка  поиска  точки  X_*   равна:

Следовательно,  число  n  итераций  метода  Фибоначчи,  необходимое  для  определения  точки  X_*   с  точностью  ε,  определяется  неравенствами:

После  N  вычислений    производится  n=N-1  итераций  и  достигается  точность  определения  X_* :

Тогда  отрезок  локализации  после  N  вычислений    достигнет  длины  [1]:

Одной  из  основных  задач  методов  прямого  поиска  является  сокращение  отрезков  локализации  на  каждой  итерации.  Поэтому  эффективность  метода  можно  оценить  тем,  во  сколько  раз  уменьшается  первоначальная  длина  интервала  после  использования  N  вычислений  значений  функции.  Таблица  1  позволяет  сравнить  по  этому  критерию  рассмотренные  методы. 

Таблица  1.

Значения  длин  отрезков  локализации Δ_N   после  N  вычислений  f(x)  на  отрезке  длиной  1

Эффективность  методов  минимизации  можно  также  сравнивать  по  гарантированной  точности  ε(N)  нахождения  точки  x_*,  которую  они  обеспечивают  в  результате  определения  N  значений  f(x).  Значения  гарантированной  точности  в  зависимости  от  количества  найденных  значений  целевой  функции,  заданной  на  отрезке  длиной  1,  представлены  в  таблице  2.

Таблица  2.

Значения  точности ε(N)  в  зависимости  от  количества  N  значений  f(x)  на  отрезке  длиной  1

Одним  из  сравнительных  показателей  качества  метода  является  количество  N  значений  функции,  которое  нужно  вычислить  для  решения  задачи  с  заданной  погрешностью ε.  Чем  это  число  меньше,  тем  при  прочих  равных  условиях  эффективнее  метод.  Во  многих  практических  случаях  определение  значений  целевой  функции  требует  больших  затрат  (например,  времени  ЭВМ  или  средств  для  проведения  экспериментов).  Сравнить  эффективность  методов  по  этому  критерию  можно  с  помощью  таблицы  3.

Таблица  3.

Количества  N   вычисленных  значений  f(x)  на  отрезке  длиной  1  в  зависимости  от  точности ε

Как  видно  из  приведенных  таблиц,  наиболее  эффективными  являются  методы  золотого  сечения  и  Фибоначчи.  В  этих  методах  происходит  исключение  отрезков,  и  необходимо  выбирать  только  одну  пробную  точку  на  итерации.  Стоит  отметить,  что  к  недостаткам  методов  золотого  сечения  и  Фибоначчи,  связанным  с  непосредственным  их  применением  к  практическим  задачам,  следует  отнести  то,  что  числа       являются  рациональными  числами,  вычисляемыми  лишь  приближенно,  и  значит,  возможно  накопление  погрешности  метода,  особенно  при  больших  n.

Следующий  по  эффективности  идет  метод  дихотомии.  Здесь  происходит  деление  отрезка  почти  пополам,  но  необходим  выбор  двух  пробных  точек  на  итерации.  Следовательно,  на  каждой  итерации  надо  вычислять  значения  целевой  функции  в  двух  пробных  точках.  Это  небольшой  недостаток,  если  функция  проста  и  вычисление  ее  значения  не  связано  с  большим  объемом  вычислений  или  проведением  дорогостоящего  эксперимента  и  т.  д.  Но  он  становится  существенным,  если  имеет  место  хотя  бы  одна  из  вышеописанных  ситуаций.  Возможно  даже,  что  число  вычислений  значений  функции  не  должно  из  соображений  дороговизны  превышать  заданного  числа  n,  и  тогда  неравенство  (5)  жестко  зафиксирует  погрешность  определения  значения  X_* ,  которая  вполне  может  оказаться  недостаточной.

Наименее  эффективным  является  метод  перебора,  при  котором  исключения  отрезков  не  применяются  вовсе.  К  существенным  недостаткам  данного  метода  относится  значительное  число  повторных  вычислений  значений  целевой  функции,  что,  как  уже  было  отмечено  выше,  во  многих  практических  случаях  может  потребовать  больших  затрат.  Однако  стоит  отметить,  что  метод  перебора  позволяет  найти  глобальный  экстремум  и  в  случае,  когда  целевая  функция  —  многоэкстремальная  функция,  что,  несомненно,  можно  отнести  к  достоинствам  этого  метода.

Список  литературы:

1.Амосов  А.А.,  Дубинский  Ю.А.,  Копченова  Н.В.  Вычислительные  методы  для  инженеров:  учеб.  пособие  —  М.:  Высш.  шк.,  1994.  —  544  с.

2.Васильев  Ф.П.  Численные  методы  решения  экстремальных  задач.  —  М.:  Наука,  1988.  —  552  с.

3.Гончаров  В.А.  Методы  оптимизации:  учеб.  пособие.  М.:  Изд-во  Юрайт;  Высшее  образование,  2010.  —  191  с.