ПРИМЕРЫ  ПОСТРОЕНИЯ  КОМПЬЮТЕРНЫХ  МОДЕЛЕЙ  В  ОБУЧЕНИИ  СТУДЕНТОВ  ЭКОНОМИЧЕСКИХ  НАПРАВЛЕНИЙ

Бунегина  Вера  Александровна

канд.  физ.-мат.  наук,  Ярославский  филиал  Московской  Академии  Предпринимательства  при  Правительстве  Москвы,  РФ,  г.  Ярославль

E -mail:  xsw4550@mail.ru

Борисова  Елена  Александровна

канд.  техн.  наук,  доцент,  Костромской  государственный  технологический  университет,  РФ,  г.  Кострома

EXAMPLES  OF  COMPUTER  MODELS  COMPOSITIONS  IN  TEACHING  STUDENTS  OF  ECONOMIC  SPECIALIZATIONS

Vera  Bunegina

candidate  of  Physical  and  Mathematical  Sciences,  Yaroslavl  Branch  of  Moscow  Academy  of  Entrepreneurship  affiliated  to  the  Government,  Russia,  Yaroslavl

Elena  Borisova

candidate  of  Technical  Sciences,  Associate  Professor,  Kostroma  State  University  of  Technology,  Russia,  Kostroma

АННОТАЦИЯ

В  статье  рассматриваются  методы  построения  компьютерных  моделей,  которые  могут  быть  использованы  для  поддержки  лекционных  и  практических  занятий  по  курсам  «Теория  вероятностей  и  математическая  статистика»,  «Теория  игр»,  «Экономико-математические  модели  и  методы»,  изучаемых  студентами  экономических  направлений,  а  также  для  формирования  познавательного  интереса  школьников  в  рамках  факультативных  занятий.

ABSTRACT

The  article  deals  with  methods  of  computer  models  compositions  which  can  be  used  on  lectures  and  seminars  devoted  to  “The  theory  of  probability  and  mathematical  statistics”,  “Game  theory”,  “Economic  and  mathematical  models  and  methods”  studied  by  students  of  economic  specializations,  and  for  the  formation  of  pupils’  cognitive  interest  within  facultative  studies.

Ключевые  слова:   формирование  профессиональных  компетенций;  компьютерное  моделирование;  теория  игр. 

Keywords :  formation  of  professional  competence;  computer  modeling;  game  theory. 

Федеральный  государственный  образовательный  стандарт  высшего  профессионального  образования  по  направлению  подготовки  080100  Экономика  (квалификация  (степень)  «бакалавр»)  в  качестве  одного  из  проектируемых  результатов  освоения  дисциплин  математического  цикла  выдвигает  требование  овладения  методикой  построения,  анализа  и  применения  математических  моделей  для  оценки  состояния  и  прогноза  развития  экономических  явлений  и  процессов.

Таким  образом,  перед  преподавателями  математических  дисциплин  стоит  непростая  задача:  в  условиях  дефицита  времени  дать  студентам  знания  своего  предмета  и  при  этом  «привязать»  эти  знания  к  реальным  процессам,  научив  студентов  моделировать  (просчитывать,  прогнозировать)  эти  процессы. 

Как  правило,  дисциплины  математического  цикла  изучаются  на  младших  курсах  и  моделирование  экономических  явлений  здесь  затруднительно  в  виду  неподготовленности  студентов  в  профессиональном  смысле.  Поэтому,  с  нашей  точки  зрения,  компромиссным  решением  может  стать  моделирование  игровых  ситуаций,  которые  легко  понимаются  обучающимися.  Такой  подход  позволяет,  что  называется  «подержать  в  руках»  математические  методы  моделирования  и  прогнозирования. 

В  качестве  примеров  моделирования  подобных  игровых  ситуаций  мы  предлагаем  рассмотреть  несколько  задач.

При  изучении  вероятностного  подхода  в  теории  игр  по  нашему  мнению  полезно  отталкиваться  от  статистического  определения  вероятности  выигрыша.  Вероятность,  прежде  всего,  связана  со  случайностью.  Обычно  студенты  относятся  к  случайности  как  к  чему-то  определяемому  свыше.  Большинство  из  них  при  этом  склонно  считать,  что  человек  хорошо  приспособлен  к  тому,  чтобы  действовать  в  условиях  неполного  знания.  Не  отвергая  этого  в  принципе,  все  же  стоит  отметить,  что  в  условиях  достаточного  количества  времени  на  построение  математической  модели,  разумно  сравнивать  свои  предположения  с  вычисляемыми  результатами. 

Одним  из  примеров,  показывающих,  что  в  ситуациях,  когда  речь  идет  о  случайных  процессах  интуиция  людей  часто  подводит,  является  парадокс  Монти  Холла.

Напомним  условия  игры:  «Имеются  три  закрытых  двери,  за  одной  из  них  находится  автомобиль,  за  двумя  другими  —  козлы.  Игрок,  выбирает  одну  из  дверей,  не  открывая  ее.  Ведущий  игры  знает,  где  находится  автомобиль  и  поэтому  после  того,  как  игрок  определился  с  выбором,  открывает  одну  из  оставшихся  дверей,  за  которой  находится  козел.  Увеличатся  ли  шансы  игрока  выиграть  автомобиль,  если  он  изменит  свой  первоначальный  выбор  и  укажет  на  вторую  закрытую  дверь?» 

При  рассмотрении  этого  парадокса  можно  провести  эксперимент,  пользуясь  пакетом  Excel.

Предлагаем  провести  1000  испытаний,  исходя  из  условия,  что  автомобиль  может  находиться  за  любой  из  трех  дверей  и  выбор  двери  игроком  производится  случайным  образом.  Для  организации  случайного  выбора  используется  встроенная  функция  СЛУЧМЕЖДУ. 

В  первом  случае  игрок  не  меняет  свой  первоначальный  выбор.

Процесс  построения  модели  представлен  на  схеме  1.

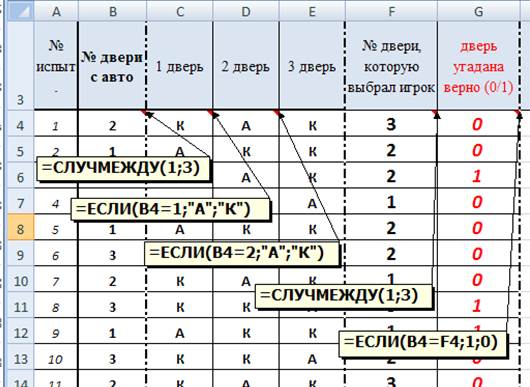
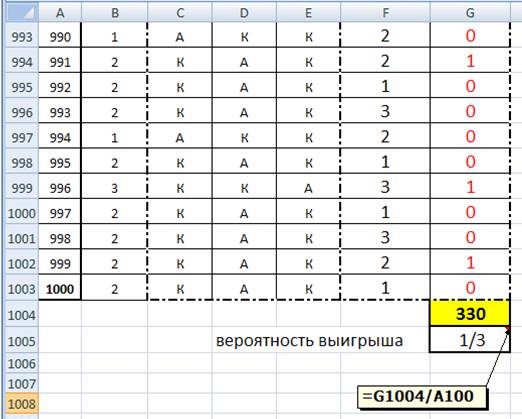
Схема  1.  Расчет  вероятности  выигрыша  в  случае  сохранения  первоначального  выбора

Функция  СЛУЧМЕЖДУ  в  Excel  хороша  тем,  что  при  нажатии  на  клавишу  Enter,  данные  в  столбцах  B  и  F  меняются  произвольно,  и  легко  видеть,  что  при  достаточно  большом  количестве  испытаний  вероятность  выигрыша  является  устойчивой  величиной. 

Теперь  предположим,  что  игрок  будет  менять  свое  решение  в  том  случае  если  ведущий,  после  его  выбора  будет  открывать  дверь,  за  которой  стоит  козел.

Вычисляем  количество  выигрышей  по  столбцу  N  (схема  2).

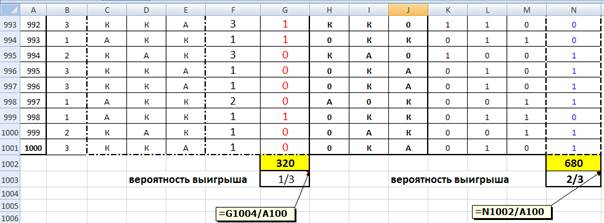
Схема  2.  Вычисление  вероятности  выигрыша  в  случае  изменения  первоначального  выбора

Таким  образом,  через  статистическое  вычисление  вероятности,  мы  подошли  к  выводу  он  том,  что  выигрыш  будет  более  вероятен,  в  случае  если,  выбор  игрока  будет  меняться.  Полезно  предложить  продолжить  решение  задачи,  при  условии,  что  игрок  случайным  образом  может  либо  сохранять  свой  первоначальный  выбор  либо  менять  его  после  предложения  ведущего.  Вероятность  выигрыша  при  этом  будет  равна  ½. 

Еще  одним  хорошим  примером  является  следующая  задача.  Группе  студентов  предлагается  задумать  число  от  1  до  400.  Преподаватель  предлагает  сделать  ставки  на  то,  что  хотя  бы  два  числа  совпадут.  Обычно  выиграть  довольно  легко,  но  сам  по  себе  выигрыш  мало  о  чем  говорит.  Поэтому  опять-таки  полезно,  с  помощью  Excel  поставить  такой  математический  эксперимент,  который  убедит  учащихся  в  том,  что  если  в  группе  25  человек,  то  вероятность  выигрыша  и  проигрыша  примерно  одинакова,  с  увеличением  числа  играющих  до  60  вероятность  выигрыша  приближается  к  единице  (схема  3). 

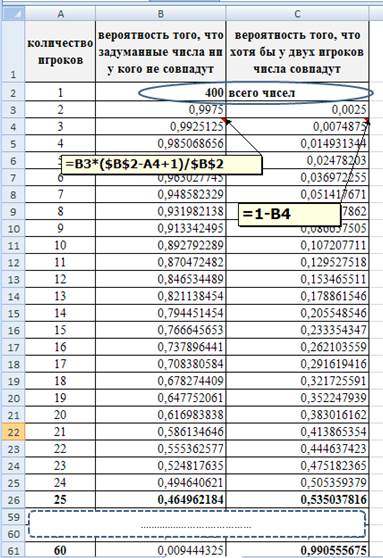
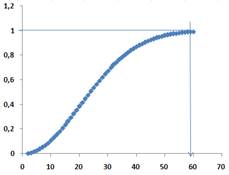
Схема  3.  Расчет  вероятности  совпадения  задуманных  чисел

Следующая  серия  примеров  помогает  убедиться  в  том,  что  из  равновероятных  возможностей,  отнюдь  не  следует  равновероятный  успех. 

Запускаем  генератор  случайного  выбора  между  0  и  1,  играем  в  500  шагов,  на  каждом  шаге  подсчитывая  число  выпавших  ранее  нулей  и  единиц.  Если  выпало  больше  единиц  то  рубль  платит  игрок  А,  если  больше  нулей,  то  игрок  Б,  если  нулей  и  единиц  поровну,  то  на  данном  шаге  ничья.  Преподаватель  может  сделать  ставку  8:1,  что  кто-то  из  игроков  выиграет  не  менее  400  рублей  и  предложить  сделать  различные  ставки  студентам,  для  простоты  устанавливая  коридоры  выигрыша  в  100  рублей. 

Эксперимент  ставится  следующим  образом  (схема  4): 

Схема  4.  Расчет  суммы  выигрыша  (проигрыша)  в  игре  с  нулями  и  единицами

Другим  привлекающим  внимание  студентов  экспериментом  является  моделирование  закона  арксинуса.

С  помощью  функции  СЛУЧМЕЖДУ(0;  1)  проводим  500  испытаний.  Конечно  данный  генератор  не  очень  качественный,  но  в  нашем  случае  это  не  особенно  важно.  Считаем,  что  если  выпала  1  то  игрок  получает  рубль  (по  другой  игре  два  рубля),  а  если  выпал  0  то  игрок  отдает  рубль  (по  другой  игре  два  рубля),  суммируем  выигрыши  и  проигрыши.  Как  следует  из  закона  арксинуса  в  80  %  случаев  игрок  будет  либо  в  выигрыше,  либо  в  проигрыше,  а  не  на  уровне  близком  к  нулевому,  как  можно  было  бы  ожидать  исходя  из  равновероятности  выпадения  орла  и  решки.  (схема  5). 

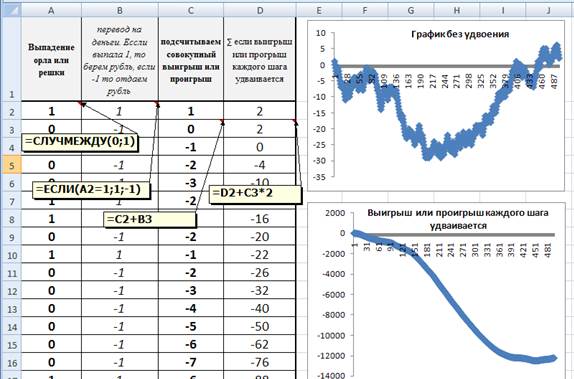
Схема  5.  Модель  закона  арксинуса

На  самом  деле  этот  закон  удивителен  сам  по  себе,  и  конечно  эксперимент  с  монетами  просто  позволяет  его  почувствовать.  Здесь  уместно  поговорить  и  том,  что  жизнь  вполне  себе  полосатая,  поскольку  зависит  от  многих  случайных  величин,  однако  какой-либо  фатализм  неуместен.  Любое  движение  может  все  изменить  как  в  лучшую,  так  и  в  худшую  сторону.

Рассмотренные  примеры  на  наш  взгляд,  являются  интересными  и  поучительными  и  способствуют  формированию  устойчивых  навыков  работы  с  широко  используемым  экономистами  пакетом  Excel. 

Список  литературы:

1.Актуальные  вопросы  образования,  науки  и  инноваций  в  свете  решения  социально-экономических  проблем.  Часть  II.  Педагогико-психологические  аспекты  развития  высшего,  среднего  специального  и  среднего  общего  образования.  Методики,  обсуждения,  предложения:  научная  монография;  [под  ред.  С.М.  Ахметова].  Новосибирск:  Изд.  «СибАК»,  2014.  —  144  с.

2.Колмогоров  А.Н.  Алгоритм,  информация,  сложность.  М.,  1991.  (МК).

3.Секей  Г.  Парадоксы  в  теории  вероятностей  и  математической  статистике.  Москва  «Мир»,  1990.

4.Феллер  В.  Введение  в  теорию  вероятностей  и  ее  приложения.  Москва  «Мир»,  том  1,  2  1984.