ОБ  ОДНОЙ  МАТЕМАТИЧЕСКОЙ  МОДЕЛИ  ДИНАМИКИ  ВОЗРАСТНОЙ  СТРУКТУРЫ

Кайгермазов  Арслан  Ахматович

канд.  физ.  мат.  наук,  доцент  КБГУ,  РФ,  г.  Нальчик

Кудаева  Фатимат  Хусейновна

канд.  физ.  мат.  наук,  доцент  КБГУ,  РФ,  г.  Нальчик

e -mail: 

ABOUT  THE  MATHEMATICAL  MODEL  OF  THE  DYNAMICS  OF  THE  AGE  STRUCTURE  OF  THE  POPULATION

Arslan  Kaygermazov

candidate  of  physical-mathematical  sciences,  associated  professor  of  Kabardin-Balkar  State  University  named  after  Kh.M.  Berbekov,  Russia,  Nalchik

Fatimat  Kudaeva

candidate  of  physical-mathematical  sciences,  associated  professor  of  Kabardin-Balkar  State  University  named  after  Kh.M.  Berbekov ,  Russia,  Nalchik

АННОТАЦИЯ

В  работе  рассмотрены  лимитированная  и  нелимитированная  математические  модели  динамики  численности  популяции.  Доказаны  теоремы  существования  и  единственности  решения  соответствующих  нелокальных  краевых  задач  и  леммы  о  стационарных  решениях  моделей.  Для  частного  случая  построено  аналитическое  решение  задачи.  В  работе  использован  аппарат  дифференциальных  и  интегральных  уравнений,  а  также  теория  интегральных  неравенств.

ABSTRACT

The  paper  deals  with  limited  and  unlimited  using  mathematical  models  of  population.  The  theorems  of  existence  and  uniqueness  of  solutions  of  nonlocal  problems  and  lemma  on  the  models  stationary  solutions.  For  the  special  case  built  analytical  solution.  Used  in  the  apparatus  of  differential  and  integral  equations  and  the  theory  of  integral  inequality.

Ключевые  слова :  популяция;  возраст;  возрастная  структура;  стационарные  состояния;  рождаемость;  смертность;  закон  рождаемости;  максимальный  возраст;  нелокальное  условие;  лимитирование.

Keywords :  population;  age  structure;  the  stationary  state;  fertility;  mortality;  the  law  of  fertility;  the  maximum  age;  illegal  conditions;  limitation.

1.  Не  лимитированная  популяционная  модель,  учитывающая  эффект  «насыщения»

В  области    рассмотрим  следующую  задачу  [1]:

Задача  1 .  Найти  непрерывное  решение  уравнения

,                                          (1)

удовлетворяющее  условиям

,                                                   (2)

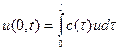.                                   (3) 

Здесь    —  численность  популяции  возраста    в  момент  времени  ;    —  коэффициент  смертности;    —  коэффициент  рождаемости;    —  максимально  возможное  значение  численности  популяции  в  данной  экологической  нише;    —  максимальный  возраст  популяции,  т.  е.  особей  старше  возраста    в  популяции    нет;    —  функция  начального  возрастного  распределения.

Нелокальное  условие  (3)  называется  законом  рождаемости.  Кроме  того,  без  ограничения  общности,  считается,  что  в  процессе  воспроизводства  участвуют  особи  всех  возрастов.

Задача  (1)—(3)  описывает  динамику  возрастной  структуры  нелимитрованной  популяции.

Предположим,  что  рождаемость  популяции  является  внешней  характеристикой  и  не  зависит  от  ее  численности.  Тогда  имеем:

,                                                 (4)

где:    —  известная  функция.

Справедливы  следующие

Лемма  1.   Пусть  выполнены  условия

1. 

2. 

Тогда,  задача  (1),  (2),  (4)  имеет  единственное,  регулярное  в  области    решение.

Лемма  2.   Пусть  выполнены  условия

1. 

2. 

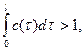
3. 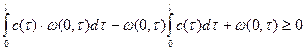 ,  при            (5)

Тогда  задача  (1)-(3)  имеет  единственное  неотрицательное  стационарное  состояние.

Здесь  .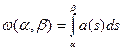

Теорема  1.   [2]  Пусть  выполнены  условия

a.   ,

b.  .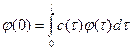

Тогда  задача  (1)—(3)  имеет  единственное  непрерывное  в  области    решение.

Отметим,  что  наличие  условия  b)  гарантирует  гладкость  искомых  решений  вдоль  характеристики  .  Если  это  условие  нарушено,  то  решение  задачи  (1)—(3)  можно  искать,  например,  в  классе  интегрируемых  или  ограниченных  функций.

Пример  1 .  В  области    рассмотрим  задачу

,                                            (6)

,                                                              (7)

,                                      (8)

где:    —  неотрицательные  константы,  причем  .

Задача  (6)—(8)  имеет  решение

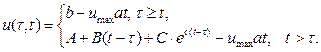                      (9)

где 

Из  (9)  следует,  что  при  выполнении  условия    решение  будет  непрерывным  при  .

2.  Лимитированная  за  счет  рождаемости  популяционная  модель  с  возрастной  структурой  учитывающая  эффект  «насыщения»

Предположим,  что  популяция    лимитирована  за  счет  ограничений  на  рождаемость.  Тогда  закон  рождаемости  будет  иметь  вид:

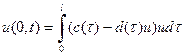.             (10) 

Здесь    —  коэффициент  рождаемости;    —  коэффициент  лимитирующий  рождаемость.

Задача  2.   Найти  непрерывное  в  области    решение  уравнения  (1)  удовлетворяющее  условиям  (2),  (10).

Справедлива 

Лемма  3.   Пусть  выполнены  условия

1. 

2.    

Тогда,  если    то  задача  2  имеет  два  стационарных  состояния;  если    то  задача  2  имеет  одно  стационарное  состояние;  если    то  задача  2  не  имеет  стационарных  решений. 

Здесь 

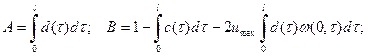
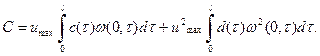
Постоянная  М  удовлетворяет  уравнению 

Пример  2.   В  области    рассмотрим  задачу:

,                                                (11)

,                                                   (12)

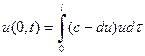,           (13)

где:  a,b,c  —  постоянные,  причем  a,b,c. 

Находим:    

Таким  образом,  если  параметры  системы  (11)—(13)  удовлетворяют  условию    то  задача  (11)—(13)  имеет  стационарные  решения  (один  или  два).  При  этом  для  не  отрицательности  этих  решений  необходимо,  чтобы  корни    удовлетворяли  условию  .

Вернемся  к  исследованию  нелокальной  задачи  2.  Введем  обозначения

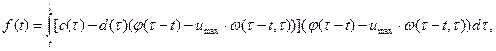
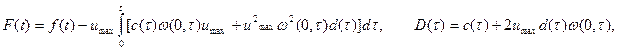
Справедлива 

Теорема  2.   Пусть  выполнены  условия

a.  ,

b.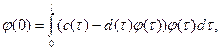 

c.   оператор    непрерывен  по    при  каждом  фиксированном    и  удовлетворяет  условию  Липшица  с  константой    то  есть 

Тогда  задача  2  имеет  единственное  непрерывное  в  области    решение.

Отметим,  что  наличие  условия  b)  гарантирует  гладкость  искомых  решений  вдоль  характеристики  .  Если  это  условие  нарушено,  то  решение  задачи  2  можно  искать,  например,  в  классе  интегрируемых  или  ограниченных  функций.

Замечание.   Если    при  ,  то  решение  задачи  2  будет  также  не  отрицательным. 

3.  Лимитированная  за  счет  сбора  «урожая»  популяционная  модель  с  возрастной  структурой  учитывающая  эффект  «насыщения»

Пусть  популяция  лимитирована  за  счет  сбора  «урожая».  Тогда  динамика  его  возрастной  структуры  удовлетворяет  уравнению

                          (14)

Здесь    —  некоторое  число,    —  фиксированный  возраст. 

Уравнение  (14)  описывает  динамику  возрастной  структуры  лимитированной  популяции.  Лимитирование  в  данном  случае  осуществляется  за  счет  слагаемого  ,  которая  характеризует  величину  сбора  “урожая”  возраста    в  момент  времени  t.

Задача  3.   Найти  непрерывное  в  области    решение  уравнения  (1)  удовлетворяющее  условиям  (2),  (3).

Стационарные  состояния  задачи  3  совпадают  с  не  отрицательными  решениями  задачи

  (15)

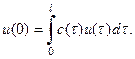  (16)

Интегрируя  уравнение  (15)  получим:

  (17)

где  М  –  произвольная  константа.

Согласовав  (17)  с  условием  (16)  получим:

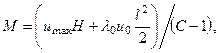  (18)

где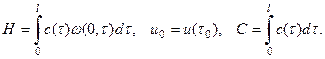 

Подставив  (18)  в  (17)  находим:

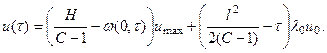  (19)

Считая  в  (19)    имеем:

  (20)

где 

Подставив  (20)  в  (19)  получим:

  (21)

Рассмотрим  теперь  задачу  3.  Учитывая,  что 

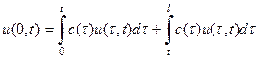
имеем:

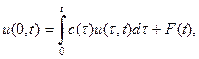  (22)

где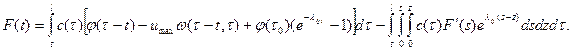    

Учитывая  (22)  получим:

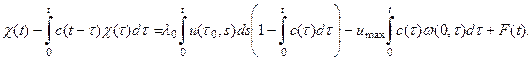  (23)

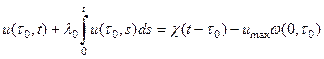  (24)

Таким  образом,  решение  задачи  3  редуцировано  к  решению  системы  интегральных  уравнений  (23)—(24)  относительно  интенсивности  рождения  новых  особей    и  численности  популяции  возраста  ,  т.  е.  .

Список  литературы :

1.Кайгермазов  А.А.,  Кудаева  Ф.Х.  Дискретные  и  непрерывные  модели  математической  биологии:  учебно-методическое  пособие.  Нальчик:  Кааб-Балк.  ун-т,  2010.  —  114  с.

2.Кайгермазов  А.А.,  Сайег  Т.Х.  Об  одной  математической  модели  с  возрастной  структурой  //  Нелинейные  проблемы  дифференциальных  уравнений  и  математической  физики.  Киев,  1997.  —  с.  130—132.