УСЛОВИЯ  УСТОЙЧИВОСТИ  СОСТОЯНИЙ  ДВИЖЕНИЯ

Королев  Владимир  Степанович

канд.  физ.-мат.  наук,  доцент,

Санкт-Петербургский  Государственный  Университет, РФ,  г.  Санкт-Петербург

E-mail:  vokorol@bk.ru

Потоцкая  Ирина  Юрьевна

канд.  физ.-мат.  наук,  доцент,

Санкт-Петербургский  Государственный  Университет, РФ,  г.  Санкт-Петербург

E-mail:  irinapototskaya@yandex.ru

Conditions  stability  of  the  movements

Vladimir  Korolev

candidate  of  Physical  and  Mathematical  Sciences,  assistant  professor,

Saint-Petersburg  State  University, Russia,  Saint-Petersburg

Irina  Pototskaya

candidate  of  Physical  and  Mathematical  Sciences,  assistant  professor,

Saint-Petersburg  State  University, Russia,  Saint-Petersburg

Аннотация

Рассматриваются  математические  модели  динамических  систем  на  основе  нелинейных  дифференциальных  уравнений,  свойства  их  решений,  условия  устойчивости  и  поведение  решений  в  окрестности  положений  равновесия  или  стационарных  состояний.  При  исследованиях  учтено  изменение  устойчивости  решений  в  зависимости  от  постановки  задачи  и  преобразования  уравнений,  которые  описывают  процесс. 

Abstract

We  consider  mathematical  models  of  dynamic  systems  based  on  non-linear  differential  equations,  properties  of  their  solutions,  the  conditions  of  stability  and  behavior  of  solutions  in  a  neighborhood  of  equilibrium  points  or  stationary  states.  In  studies  into  account  changes  in  the  stability  of  solutions  depending  on  the  problem  definition  and  the  transformation  equations  that  describe  the  process.

Ключевые  слова:  динамические  системы;  устойчивость  решений.

Key  words:  dynamical  systems;  stability  of  solution.

Введение.

Под  динамической  системой  подразумевается  изменение  состояния  процесса  во  времени.  Если  результаты  наблюдений  или  измерений  позволяют  однозначно  определить  значения  параметров  системы,  то  говорят  о  детерминированных  динамических  системах.  Если  параметры  или  дополнительные  воздействия  можно  выбирать  по  своему  усмотрению,  то  имеют  управляемую  систему.  Многие  сложные  процессы  классической  механики  моделируются  системами  обыкновенных  дифференциальных  уравнений  [1;  2].  При  исследовании  поведения  нелинейных  динамических  систем  важно  знать  основные  свойства  решений:  существуют  ли  состояния  равновесия  или  покоя,  какие  из  них  устойчивы,  возможны  ли  колебательные  режимы  движения  и  при  каких  условиях  [3–6].  Равновесие  определяют  как  состояние  системы,  когда  одни  силовые  воздействия  компенсируются  другими  или  вообще  отсутствуют.  Состояние  покоя  означает  сохранение  положения  всех  элементов  механической  системы  относительно  некоторой  системы  отсчета  [7–13;  18].

Наличие  даже  малых  возмущений  периодического  или  случайного  характера  может  изменить  характер  решений  таких  систем.  Поэтому  поведение  и  свойства  решений  динамических  систем,  моделирующих  управляемые  процессы,  определяются  главным  образом  выбранными  управляющими  воздействиями  [4;  6;  8].  При  этом  анализируется  вид  полученной  устойчивости  [9;  10]  и  методы  исследования  нелинейных  непрерывных  или  дискретных  систем,  которые  могут  определять  качество  движений:  абсолютная  или  асимптотическая  устойчивость,  по  первому  приближению  или  в  целом.

В  зависимости  от  начальных  условий  и  значений  коэффициентов  системы  уравнений  в  качестве  отклика  на  приложенный  импульс  или  серию  импульсов  могут  проявляться  устойчивые  и  неустойчивые  колебательные  режимы  по  соответствующим  группам  переменных.  Каждое  из  возможных  устойчивых  положений  равновесия  определяет  область  пространства,  заполненное  траекториями  движения  системы.

Определения  устойчивости.

На  основе  первого  закона  Ньютона  можно  определить  состояние  равномерного  прямолинейного  движения  или  покоя  для  свободной  материальной  точки  относительно  инерциальной  системы  координат  условием,  если  на  точку  не  действуют  никакие  силы  или  их  векторная  сумма  равна  нулю  [2;  13;  18]

Mw  =  F  =0.                                                         (1)

При  этом  принцип  относительности  Галилея  утверждает,  что  существует  система  отсчета,  в  которой  материальная  точка  находится  в  состоянии  покоя.

Если  используется  неинерциальная  система  отсчета,  то  кроме  активных  сил  необходимо  учитывать  силы  инерции.  Когда  сумма  сил  равна  нулю,  получаем  в  этом  случае  относительное  положение  равновесия  или  покоя.  Если  рассматривается  движения  несвободной  материальной  точки  при  действии  ограничений,  то  необходимо  учитывать  пассивные  силы  реакции  связей.

При  определении  движения  твердого  тела  или  произвольной  механической  системы  кроме  основных  задач  динамики  часто  требуется  оценить  устойчивость  и  управляемость  состояний  движения.

Одним  из  первых  определение  понятия  устойчивости  было  дано  Л.  Эйлером  в  1749  г.  в  связи  с  практически  важным  вопросом  того  времени  устойчивости  кораблей  Российского  флота  (рис.  1):  «равновесное  положение  тела  будет  устойчиво,  ежели  оное  тело,  будучи  несколько  наклонено,  опять  исправится»  [8;  15].

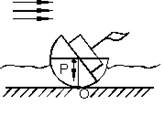
Рисунок  1.  Устойчивость  корабля  по  Эйлеру

Применительно  к  упругим  системам  определение  Эйлера  можно  сформулировать  следующим  образом:  «равновесие  в  упругой  системе  при  заданных  внешних  силах  считается  устойчивым,  если  после  статического  приложения  малой  возмущающей  силы  и  последующего  снятия  система  возвращается  к  своему  исходному  состоянию».  В  противном  случае  исходное  состояние  равновесия  системы  считается  неустойчивым.

Рисунок  2.  Устойчивость  упругой  системы

Другим,  более  общим,  определением  устойчивости  состояния  равновесия  является  определение  Лагранжа  для  упругой  системы  (рис.  2):  «исходное  состояние  равновесия  устойчиво,  если  после  отклонения  от  этого  состояния  она,  предоставленная  самой  себе,  стремится  вернуться  к  нему,  совершая  малые  колебания,  затухающие  со  временем  при  наличии  сил  внешнего  и  внутреннего  сопротивления».

Строгое  определение  понятия  устойчивости  положения  равновесия  и  других  решений  динамических  систем  было  дано  в  1892  г.  русским  ученым  А.М.  Ляпуновым  [11]. 

Движение  или  поведение  решения  динамической  системы  называется  устойчивым  по  Ляпунову,  если  малые  отклонения  в  начальных  данных  фазовых  переменных  от  опорного,  выбранного  для  исследования,  решения  системы  дифференциальных  уравнений  приводят  к  малым  уклонениям  в  дальнейшем.  Если  отклонение  со  временем  стремится  к  нулю,  то  опорное  решение  называют  асимптотически  устойчивым.

Устойчивость  определяют  по  Эйлеру,  Лагранжу,  Ляпунову,  Пуанкаре,  Жуковскому  или  Красовскому,  а  также  рассматривается  орбитальная  устойчивость  траекторий  или  устойчивость  по  части  переменных  [3;  5;  17;  19].  В  последнем  случае  оказывается,  что  фазовая  траектория  или  её  проекция  на  соответствующее  подпространство  остается  в  достаточной  близости  от  опорной  траектории,  хотя  изображающие  точки  могут  сколь  угодно  разбегаться,  удаляясь  друг  от  друга  со  временем. 

В  механике  устойчивость  характеризуется  реакцией  на  достаточно  малое  отклонение  в  начальных  данных  или  возмущение  действующих  сил  для  системы,  находящейся  в  равновесии.  Устойчивость  –  способность  системы  сохранять  текущее  состояние  равновесия  или  движения  при  влиянии  внешних  малых  воздействий.  Под  неустойчивостью  понимают  способность  систем  при  действии  весьма  малых  возмущений  получать  большие  перемещения  или  менять  характер  движения.  Процесс  считается  неустойчивым,  если  сколь  угодно  малое  возмущение  вызывает  катастрофическое  развитие  перемещений  и  деформаций.  Катастрофа  наступает  в  точках,  которые  называют  точками  бифуркации  Пуанкаре  или  пределами  устойчивости.

Наглядным  примером  устойчивого  состояния  равновесия  служит  поведение  тяжёлого  шарика  на  гладкой  поверхности  в  зависимости  от  формы  и  свойств  в  окрестности  текущего  положения.

Рисунок  3.  Устойчивость  по  Лагранжу

Если  шарик  отклонить  из  положения  покоя  и  он  начнет  колебаться  около  нижнего  положения  в  ямке,  то  состояние  равновесия  устойчиво.  В  противном  случае  –  неустойчиво.  В  том  числе  возможно  безразличное  положение  шарика  на  идеально  гладкой  горизонтальной  плоскости  (рис.  3),  которое  не  является  устойчивым,  если  начальное  значение  скорости  отличается  от  нуля.

Из  теоремы  Лагранжа-Дирихле  следует,  что  положение  равновесия  для  механической  системы  в  однородном  поле  тяжести  будет  устойчивым,  когда  центр  тяжести  системы  занимает  самое  низшее  положение.

Система  называется  устойчивой,  если  при  выведении  ее  внешними  воздействиями  из  состояния  равновесия  или  покоя  она  в  него  возвращается  после  прекращения  внешних  воздействий  при  условии,  что  механическая  система  не  испытывает  катастрофических  деформаций.  Если  после  прекращения  внешнего  воздействия  система  не  возвращается  к  состоянию  равновесия,  то  она  является  неустойчивой.

Однако  в  реальных  механических  системах  всегда  существуют  силы  сопротивления  движению,  возникающие  благодаря  трению  или  вязкости  среды.  Устойчивое  положение  равновесия  становится  асимптотически  устойчивым  при  добавлении  диссипативных  сил  с  полной  диссипацией.  Такие  силы  не  могут  неустойчивое  положение  равновесия  сделать  для  консервативной  системы  устойчивым.

Критерии  устойчивости.

В  общем  случае  системы  дифференциальных  уравнений  динамики  системы  в  нормальной  форме  имеют  особые  точки  положения  покоя  или  состояния  равновесия  при  условии,  что  правые  части  обращаются  в  ноль:

                             (2)

Существуют  различные  критерии  устойчивости,  в  том  числе  критерии  Рауса  и  Гурвица,  Найквиста  и  Михайлова,  метод  Тимошенко,  метод  Кармана,  метод  функций  Ляпунова  или  простого  экспериментального  тестирования.  Однако  этими  критериями  пользоваться  во  многих  случаях  практически  сложно  из-за  необходимости  проведения  громоздких  расчётов.  Изменения  свойств  и  также  условий  устойчивости  решений  возможны  при  переходе  к  новой  системе  уравнений  при  замене  переменных  [6;  14]. 

Свойство  траектории  или  решения    автономной  системы  обыкновенных  дифференциальных  уравнений  называется  орбитальной  устойчивостью,  если  для  всякого    существует    такое,  что  всякая  положительная  полутраектория,  начинающаяся  в  d–окрестности  траектории    при  ,  содержится  в    –  окрестности  траектории.  Здесь  под  траекторией  понимается  множество  значений  решения  ,  а  под  положительной  полутраекторией  –  множество  значений  решения    при  .  Если  решение    устойчиво  по  Ляпунову,  то  его  траектория  орбитально  устойчива.

Траектория    называется  асимптотически  орбитально  устойчивой,  если  она  орбитально  устойчива  и,  кроме  того,  найдется    такое,  что  траектория  всякого  решения    системы  (2),  начинающегося  в  –окрестности  траектории  (то  есть  при  )  стремится  при    к  траектории  .

Периодическое  решение  системы  (2)  не  бывает  асимптотически  устойчивым.  Но  если  у  периодического  решения  такой  системы  модули  всех  мультипликаторов,  кроме  одного,  меньше  единицы,  то  траектория  этого  периодического  решения,  согласно  теореме  Андронова–Витта  [1],  асимптотически  орбитально  устойчива.

Уравнения  Лагранжа  второго  рода  для  консервативных  механических  систем  позволяют  использовать  для  оценки  устойчивости  вид  функции  П(q)  для  потенциальной  энергии.  Положения  равновесия  или  возможного  положения  покоя  находится  из  условий  минимума  по  лагранжевым  или  обобщенным  переменным: 

                                         (3)

Матрица  вторых  частных  производных,  которая  вычисляется  в  положении  равновесия,  используется  для  оценки  устойчивости.  Для  системы  с  одной  степенью  свободы  требуется  определить  знак  второй  производной  П(х)  и  выделить  точки  минимума.

При  наличии  k  циклических  интегралов  порядок  системы  уравнений  уменьшается.  Получается  система  уравнений  с  функцией  Рауса  R(q),  а  устойчивость  оценивают  для  оставшихся  обобщенных  координат.

                                      (4)

При  этом  обобщенные  импульсы,  соответствующие  циклическим  координатам,  остаются  постоянными  p_i  =const  и  определяют  стационарные  движения  системы,  которые  могут  иметь  устойчивость  или  в  режиме  автоколебаний  даже  асимптотическую  устойчивость.

Постановка  задачи  об  устойчивости  движения  относительно  части  переменных  принадлежит  А.М.  Ляпунову  [12].  При  исследовании  одного  из  критических  случаев  Ляпунов  отметил,  что  «можно  рассматривать  более  общую  задачу:  об  устойчивости  того  же  движения,  но  по  отношению  не  ко  всем,  а  только  к  некоторым  из  величин».  Однако  сам  Ляпунов  данной  задачей  не  занимался.  На  замечание  А.М.  Ляпунова  обратил  внимание  И.Г.  Малкин  [7],  указавший  некоторые  условия  на  случай  устойчивости  по  части  переменных.

Устойчивостью  по  отношению  к  части  переменных  для  дифференциальных  уравнений  занимался  В.В.  Румянцев,  который  напечатал  статью  [17]  по  аналогу  теорем  второго  метода  Ляпунова  для  задач  устойчивости  по  части  переменных.  Он  со  своими  учениками  разработал  методы  исследования  задачи  устойчивости  по  части  переменных.

В  случае  приведения  уравнений  к  виду  канонических  систем  можно  проверять  аналогичные  условия  для  функции  Гамильтона  Н(х),  которая  при  дифференцировании  по  фазовым  переменным  определяет  все  правые  части  уравнений  движения. 

Необходимо  обратить  внимание  на  возможные  изменения  свойств  и  условий  устойчивости  решений  новых  уравнений  при  замене  переменных.

В  случае  контактных  преобразований  канонических  уравнений  при  выборе  для  замены  координат  нужной  производящей  функции  получаем  в  новых  переменных  (q,  p)  уравнения,  где  правые  части  равны  нулю,  а  новые  переменные  определяют  набор  произвольных  постоянных  для  решений  первоначальной  системы  канонических  уравнений  [14].  Следовательно,  при  любых  допустимых  отклонениях  в  начальных  условиях  они  остаются  постоянными,  сохраняя  малые  начальные  отклонения.

Если  уравнения  динамики  системы  записаны  в  каноническом  виде  и  существует  n  первых  интегралов,  то  по  теореме  Арнольда  [2;  6]  все  фазовые  траектории  лежат  на  n–мерном  торе,  а  движение  системы  является  условно  периодическим.  В  общем  случае  для  системы  дифференциальных  уравнений  в  нормальной  форме  могут  выполняться  первые  интегралы,  которые  определяют  интегральные  многообразия  как  пересечение  соответствующих  поверхностей.  Это  множество  называют  равновесным  или  стационарным  режимом  движения  системы.

Вопрос  об  устойчивости  является  одним  из  первых  вопросов,  возникающих  при  исследовании  и  проектировании  систем  управления.  Наличие  возмущений  и  управляющих  воздействий  может  также  влиять  на  свойства  положений  равновесия  и  возможные  стационарные  состояния.  Для  исследования  этого  влияния  в  математических  моделях  предлагаются  модификации  [6;  16]  или  дополнения,  упрощающие  оценку  устойчивости  выделенных  решений. 

Примеры  устойчивости  состояний  равновесия.

Наличие  многих  определений  и  критериев  устойчивости  может  приводить  к  затруднениям  или  неправильному  их  использованию.

Наиболее  просто  и  наглядно  методы  исследования  устойчивости  решений  демонстрируются  на  примере  системы  дифференциальных  уравнений  математического  маятника  при  движении  в  вертикальной  плоскости  при  действии  силы  тяжести: 

                   (5)

Потенциальная  энергия  задачи  может  иметь  вид  .  Это  позволяет  получить  фазовые  траектории  с  помощью  интеграла  энергии.

Получаются  особые  точки,  которые  на  фазовой  плоскости  окружают  замкнутые  кривые  периодических  колебаний.  Находим  состояния  равновесия,  равные  значениям  угла,  которым  отвечают  устойчивые  положения  в  точках  минимума,  или  ,  которым  соответствуют  неустойчивые  положения. 

Если  ограничиваться  линейным  приближением,  то  уравнение  превращается  в  уравнение  гармонических  колебаний  или  гармонического  осциллятора

.                                                     (6)

Период  линейного  приближения  не  зависит  от  начальных  условий.  Поэтому  малые  колебания  математического  маятника  будут  изохронными.

.                                     (7)

Рисунок  4.  Фазовый  портрет  для  математического  маятника

Движение  механической  системы  или  положение  покоя  относительно  неинерциальной  системы  отсчета  учитывает  силы  инерции.  Для  случая  движения  материальной  точки  по  направляющей,  которая  вращается  с  постоянной  угловой  скорость  p  =  сonst  вокруг  вертикальной  оси,  получаем

                                    (8)

При  наличии  малых  отклонений  от  положения  относительного  покоя  или  при  действии  возмущений  и  управлений  система  уравнений  имеет  вид:

                      (9)

тогда  решение  представляет  сумму  общего  решения  однородного  и  частного  решения  неоднородного  уравнения  с  учетом  возмущений:

    (10)

Для  случая  свободного  движения  материальной  точки  в  однородном  поле  силы  тяжести  по  поверхности  сферы  без  учета  действия  других  сил  получим  при  использовании  сферических  координат  систему  уравнений:

                                      (11)

Циклический  интеграл  определяет  изменение  угловой  скорости    при  отклонении  от  вертикали,  хотя  траектория  остается  близкой  к  начальной.  Получаем  орбитальную  устойчивость  движения  точки  или  устойчивость  по  части  переменных.

В  механической  системе  существуют  силы  сопротивления  движению,  возникающие  благодаря  трению  или  вязкости  среды  [8].  Такие  силы  называют  диссипативными.

Теорема  (Кельвин)  утверждает:  Диссипативные  силы  с  полной  диссипацией  делают  устойчивое  положение  равновесия  или  точки  покоя  асимптотически  устойчивыми.

Малые  колебания  для  стационарного  движения  в  окрестности  устойчивого  относительного  положения  равновесия  также  могут  быть  устойчивыми  решениями  (в  некоторой  области)  для  системы  уравнений,  но  к  ним  нельзя  применить  теорему  Кельвина.

Теорема  (Королев).  Диссипативные  силы  делают  устойчивое  стационарное  движение  в  окрестности  устойчивого  относительного  положения  равновесия  или  стационарного  движения  системы  неустойчивым.

Особенностью  системы  уравнений  является  существование  первых  интегралов,  которые  позволяют  понизить  порядок  или  проводить  дальнейшее  исследование  устойчивости  по  упрощенным  уравнениям  для  оставшихся  фазовых  переменных  после  исключения.  Это  позволяет  получить  критерии  условной  устойчивости  по  части  переменных  [3;  7;  17]  для  начальной  системы,  а  также  критерии  устойчивости  для  упрощенной  системы  в  первом  приближении. 

Примеры  устойчивости  по  части  переменных.

Если  уравнения  динамики  системы  записаны  в  каноническом  виде  и  существует  k  первых  интегралов,  то  по  теореме  Арнольда  [6;  7;  19;  20]  фазовые  траектории  лежат  на  k  –  мерном  многообразии.  Движение  системы  является  условно  периодическим.  В  общем  случае  для  системы  дифференциальных  уравнений  в  нормальной  форме  могут  выполняться  первые  интегралы,  которые  определяют  интегральные  многообразия  как  пересечение  соответствующих  поверхностей.  Это  множество  называют  равновесным  или  стационарным  режимом  системы.

Наличие  возмущений  и  управляющих  воздействий  может  также  влиять  на  свойства  положений  равновесия  и  возможные  стационарные  равновесные  состояния.  Известны  математические  модели  [2;  6;  16]  в  задачах  взаимодействия  видов  Лотки  или  Вольтера: 

                                     (12)

Система  имеет  два  стационарных  решения.  В  том  числе  получается  особая  точка,  которую  на  фазовой  плоскости  окружают  замкнутые  кривые  периодических  колебаний  численности  конкурирующих  видов  в  зависимости  от  параметров  системы  и  начальных  условий.  Модификацию  модели  с  учетом  самоограничения  численности,  которую  предложил  Базыкин,  можно  представить  в  виде  системы  уравнений:

       (13)

Начало  координат  является  особой  точкой  типа  «неустойчивый  узел».  Существуют  еще  три  варианта  возможных  особых  точек.  Для  учета  влияния  возмущений  или  управлений  предлагаются  модификации  и  дополнения,  упрощающие  оценку  устойчивости  выделенных  решений.  В  зависимости  от  начальных  условий  и  значений  коэффициентов  уравнений  могут  проявляться  устойчивые  или  неустойчивые  колебательные  режимы.

Уравнения  можно  представить  в  общем  виде,  где  возмущения  зависят  от  управляющих  параметров  или  функций  u(t).  В  правой  части  системы  нелинейных  уравнений  можно  выделить  линейную  и  квадратичную  зависимость  от  фазовых  переменных:

                                          (14)

Особенностью  задачи  является  существование  линейных  по  фазовым  переменным  интегралов,  которые  позволяют  понизить  порядок  и  проводить  дальнейшее  исследование  устойчивости  по  упрощенным  уравнениям  для  оставшихся  после  исключения  фазовых  переменных.  Каждое  из  возможных  положений  равновесия  определяет  подпространство,  заполненное  асимптотически  устойчивыми  движениями  системы.  Это  позволяет  получить  критерии  условной  устойчивости  для  начальной  системы.

Стационарные  вращения  твердого  тела.

Уравнения  Эйлера  вращения  твердого  тела  с  неподвижной  точкой  С  в  классическом  случае,  когда  она  совпадает  с  центром  масс,  имеют  первые  интегралы  [14;  18]  сохранения  энергии 

                                           (15)

и  модуля  кинетического  момента

                                                    (16)

показывают,  что  имеются  три  варианта  установившихся  движений  в  виде  стационарных  вращений  относительно  трех  главных  осей  эллипсоида  инерции,  когда  две  компоненты  угловой  скорости  равны  нулю,  а  третья  –  постоянна  [14].  Если  моменты  инерции  тела  различны  I_x  >  I_y  >  I_z  ,  то  можно  отметить  фазовые  траектории  на  поверхности  так  называемого  гирационного  эллипсоида  на  основе  уравнения  (15),  которые  получаются  при  его  пересечении  со  сферой  (16),  радиус  которой  определяет  модуль  кинетического  момента  из  начальных  условий.

При  малом  изменений  начальных  условий,  отвечающих  частным  случаям  вращения  тела  относительно  осей  Cx  и  Cz,  фазовые  траектории  будут  замкнутыми  кривыми,  охватывающими  соответствующую  ось  (рис.  5).  Это  показывает  устойчивость  стационарных  вращений.  Третий  случай  вращения  относительно  оси  Cy  показывает  неустойчивость  по  Ляпунову  так  как  фазовые  траектории  становятся  незамкнутой  и  происходит  большое  отклонение  оси  вращения  тела.

Во  многих  работах  для  задач  динамики  проводится  исследование  устойчивости  по  первому  приближению  для  системы  нелинейных  уравнений,  когда  выделяют  линейную  часть  при  разложении  функций  по  степеням  малых  отклонений  от  положения  равновесия  или  вариаций  переменных  и  затем  отбрасывают  слагаемые  более  высокого  порядка  малости.  Решение  или  анализ  системы  первого  приближения  позволяет  оценить  устойчивость  решений  исходной  системы  уравнений  или  определить  основные  свойства.

Рисунок  5.  Фазовый  портрет  вращения  тела

Например,  устойчивость  вертикального  положения  оси  «спящего  волчка»  для  случая  Лагранжа  вращения  твердого  тела  с  неподвижной  точкой,  когда  она  находится  на  оси  динамической  симметрии  ниже  центра  масс,  при  исследовании  уравнений  в  первом  приближении  [14]  позволяет  получить  достаточные  условия  устойчивости. 

С  течением  времени  в  результате  диссипации  энергии  при  действии  сил  трения  или  сопротивления  атмосферы  кинетический  момент  уменьшается,  условие  перестает  выполняться  и  «волчок  просыпается».  Происходит  отклонение  оси  вращения  от  вертикали  и  стационарное  движение  становится  неустойчивым.

Эффективным  средством  исследования  устойчивости  решений  для  многих  задач  динамики  остается  прямой  метод  функций  Ляпунова,  который  можно  дополнять  алгебраическим  или  геометрическим  аппаратом,  а  также  второй  метод  Ляпунова.  Это  находит  применение  в  актуальных  задачах  стабилизации  или  управления  для  линейных  или  нелинейных  нестационарных  систем.

Список  литературы:

1. Андронов  А.А.,  Витт  А.А.,  Xайкин  С.Э.  Теория  колебаний.  –  М.,  1959.
2. Арнольд  В.И.  Математические  методы  классической  механики.  –  М.:  Наука.  1979.  –  432  с.
3. Воротников  В.И.  К  теории  устойчивости  по  отношению  к  части  переменных  //  Прикладная  математика  и  механика.  –  Т.  59(4),  –  1995,  –  с.  553–561.
4. Гелиг  А.Х.,  Зубер  И.Е.,  Чурилов  А.Н.  Устойчивость  и  стабилизация  нелинейных  систем.  –  СПб.:  изд.  СПбГУ,  2006.  –  270  с.
5. Зубов  В.И.  Процессы  управления  и  устойчивость.  –  СПб:  Изд-во  СПбГУ,  1999.  –  325  с.
6. Зубов  И.В.  Методы  анализа  динамики  управляемых  систем.  –  М.:  Физматлит,  2003.  –  224  с.
7. Королев  В.С.  Устойчивость  решений  динамических  систем  по  части  переменных  //  Естественные  и  математические  науки  в  современном  мире.  №  6  (18).  Новосибирск:  изд.  «СибАК»,  2014,  –  с.  14–22.
8. Королев  В.С.  Вопросы  устойчивости  положений  равновесия  //  Естественные  и  математические  науки  в  современном  мире.  №  24.  Новосибирск:  изд.  «СибАК»,  2014,  –  с.  13–20.
9. Леонов  Г.А.  Странные  аттракторы  и  классическая  теория  устойчивости  движения.  –  СПб.:  изд.  СПбГУ,  2004.  –  144  с.
10. Леонов  Г.А.,  Пономаренко  Д.В.  Критерии  орбитальной  устойчивости  траекторий  динамических  систем.  //  Известия  ВУЗов.  Математика,  –  1993,  –  №  4,  –  с.  88–94.
11. Ляпунов  А.М.  Общая  задача  об  устойчивости  движения.  –  М.:  Изд-во:  «Меркурий-Пресс»,  2000.  –  386  с.
12. Ляпунов  А.М.  Исследование  одного  из  особенных  случаев  задачи  об  устойчивости  движения  //  Собрание  сочинений,  т.  2.  –  М.-Л.:  Изд-во  АН  СССР,  1956,  –  с.  272–331.
13. Маркееев  А.П.  Теоретическая  механика.  –  Ижевск:  НИЦ  «Регулярная  и  хаотическая  динамика»,  2001.  –  512  с.
14. Новоселов  В.С.,  Королев  В.С.  Аналитическая  механика  управляемой  системы.  –  СПб.:  изд.  СПбГУ,  2005.  –  298  с.
15. Поляхова  Е.Н.,  Королев  В.С.,  Холшевников  К.В.  Переводы  трудов  классиков  науки  академиком  А.Н.  Крыловым  //  Естественные  и  математические  науки  в  современном  мире.  –  №  27,  –  2015,  –  с.  108–128.
16. Романовский  Ю.М.,  Степанова  Н.В.,  Чернавский  Д.С.  Математическое  моделирование  в  биофизике.  –  Москва-Ижевск:  Институт  компьютерных  исследований,  2004.  –  472  с.
17. Румянцев  В.В.  Об  устойчивости  движения  по  отношению  к  части  переменных.  //  Вестник  МГУ.  Серия  мат.,  мех.,  физ.,  астрон.,  хим.,  –  №  4,  –  1957,  –  с.  9–16.
18. Четаев  Н.Г.  Устойчивость  движения.  –  М:  Гостехиздат,  1955.  –  207  с.
19. Korolev  V.S.,  Pototskaya  I.Yu.  Integration  of  dynamical  systems  and  stability  of  solution  on  a  part  of  the  variables.  Applied  Mathematical  Sciences,  –  vol.  9,  –  №  15,  –  2015.  –  P.  721–728.
20. Korolev  V.S.,  Pototskaya  I.Yu.  Problems  of  stability  with  respect  to  a  part  of  variables  //  International  Conference  on  Mechanics,  Seventh  Polyakhov's  Reading,  2015.  –  P.  1–4.