РАЗРАБОТКА  ПРОГРАММЫ  ДЛЯ  ПРОКЛАДКИ  ОПТИМАЛЬНОГО  МАРШРУТА  ПО  КОМПЛЕКСНОМУ  КРИТЕРИЮ  ЭФФЕКТИВНОСТИ

Муравьев  Владислав  Витальевич

студент  2  курса,  кафедра  «Автоматика  и  управление  в  технических  системах»,  СамГТУ, 
РФ,  г.  Самара

Кулагин  Иван  Николаевич

студент  2  курса,  кафедра  «Автоматика  и  управление  в  технических  системах»,  СамГТУ, 
РФ,  г.  Самара

Столбовой  Дмитрий  Александрович

студент  2  курса,  кафедра  «Автоматика  и  управление  в  технических  системах»,  СамГТУ, 
РФ,  г.  Самара

Е-mail:  tot.kto.1997@mail.ru

Тычинина  Юлия  Александровна

научный  руководитель,  канд.  техн.  наук,  доцент  СамГТУ, 
РФ,  г.  Самара

В  настоящее  время  большой  популярностью  пользуются  различные  программы  для  нахождения  оптимального  маршрута  между  двумя  объектами  на  местности.  В  качестве  критерия  для  выбора  маршрута  чаще  всего  используется  критерий  минимизации  суммарного  расстояния,  однако  в  реальности  кратчайший  по  расстоянию  путь  не  всегда  является  оптимальным  по  времени,  расходу  топлива  и  т.  п.  На  дорожную  обстановку  влияет  множество  внешних  факторов,  поэтому  свести  все  значащие  критерии  к  одному  затруднительно  ввиду  сложности  формализации  целевой  функции.

Существует  ряд  программ,  позволяющих  искать  кратчайший  путь  проезда  по  электронной  карте  [1;  3].  В  данных  программах  используются  критерии  кратчайшего  расстояния,  оценки  времени  с  учетом  информации  о  пробках.  Целью  данной  работы  было  создание  программы  для  прокладки  маршрута  по  критерию,  учитывающему  сразу  несколько  значимых  для  пользователя  факторов.

Дорожную  сеть  можно  представить  в  виде  ориентированного  взвешенного  графа  G(V,E),  где  V  –  это  множество  вершин  в  количестве  m,  E  –  множество  ребер  в  количестве  n,  каждому  ребру  поставлено  в  соответствии  некоторое  число    (вес).  Вершинам  графа  соответствуют  перекрестки  на  улицах  города,  то  есть  места  дорожной  сети,  где  имеются  возможности  выбора  дальнейшего  маршрута  поездки.  Ребрам  графа  соответствуют  участки  дорог  между  двумя  вершинами.

Из  теории  графов  известно,  что  кратчайшим  путем  из  вершины  a  в  вершину  b  будет  называться  путь  P=(V₁,  V₂,  …,  V_k),  длиной  k,  где  V₁=a,  V_k=b,  который  имеет  минимальное  значение  суммы    [2].  В  данной  работе  предлагается  ввести  для  каждого  ребра  несколько  весов,  каждый  из  которых  характеризует  один  из  факторов  важных  для  пользователя.  Например,  можно  в  качестве  веса    рассматривать  длину  j-го  ребра,    –  качество  дорожного  покрытия  соответствующего  участка,  выраженного  в  относительных  единицах  по  десятибалльной  шкале  (0  –  непроходимая  дорога,  10  –  идеальное  дорожное  покрытие),    –  загруженность  j-го  участка  дороги  по  десятибалльной  шкале  (0  –  пустая  дорога,  10  –  движение  парализовано).  Пользователь  может  задать  не  только  начальный  и  конечный  пункт  назначения,  но  и  свои  приоритеты  при  оптимизации  движения  в  виде  весовых  коэффициентов  ,  таким  образом,  чтобы  +,  например  набор  введенных  коэффициентов:    означает,  что  пользователя  в  первую  очередь  (на  60%)  интересует  минимизировать  пройденное  расстояние,  во  вторую  очередь  (на  30  %)  избежать  пробок,  а  в  последнюю  очередь  качество  дорожного  покрытия.

Таким  образом,  комплексный  критерий  оптимальности  в  задаче  нахождения  пути  можно  сформулировать  в  виде  (1):

  (1)

В  результате  данной  работы  с  помощью  Microsoft  Visual  Studio  была  написана  программа  нахождения  оптимального  по  смешанному  критерию  эффективности  маршрута  между  двумя  пунктами.  Программа  предусматривает  ввод  количества  вершин  графа,  а  также  три  матрицы  весов  ребер,  отображающих  физическую  длину  ребер,  качество  дороги  на  данном  участке  и  его  загруженность.  Ребра  графа  могут  быть  как  ориентированными  (дороги  с  односторонним  движением),  так  и  неориентированными.  Далее  вводятся  коэффициенты  приоритета  пользователя  .  После  ввода  исходных  данных  программа  визуализирует  граф,  рассчитывает  результирующую  матрицу  смежности  с  учетом  трех  исходных  матриц  весов  и  коэффициентов  приоритета.  На  следующем  этапе  пользователь  указывает  начальную  и  конечную  вершину  маршрута,  на  основе  этих  данных  программа  находит  оптимальных  путь  с  использованием  алгоритма  Дейкстры  [2],  выводит  его  стоимость  и  выделяет  маршрут  на  графическом  представлении  графа.  На  рисунке  1  представлено  главное  окно  программного  интерфейса,  которое  служит  для  ввода  исходных  данных.  В  данном  примере  коэффициенты  приоритета  расставлены  таким  образом,  что  при  выборе  траектории  учитывается  только  длина  пройденного  пути,  а  остальные  факторы  не  рассматриваются  ().  Кратчайший  путь  отображается  во  вспомогательном  окне  визуализации  графа  (рисунок  2).  На  рисунках  3–4  показан  пример  работы  программы  при  коэффициентах  приоритета  пользователя  ()  и  других  пунктах  отправки  и  назначения.

В  дальнейшем  планируется  усовершенствовать  интерфейс  программы,  добавить  привязку  к  карте  местности,  загруженной  из  внешнего  файла,  внедрить  динамический  подход,  в  ходе  которого  пользователь  сам  может  задавать  на  карте  нужное  количество  вершин  и  смешанных  критериев,  что  предало  бы  большой  гибкости  приложению,  обновление  информации  о  пробках  в  режиме  on-line,  например,  с  сервиса  яндекс-пробки.

В  качестве  значимых  факторов  можно  использовать  и  другие,  например,  информацию  по  ограничениям  скорости  на  том  или  ином  участке  дорожной  сети,  наличие  на  перекрестках  светофоров  и  временные  интервалы  смены  их  сигналов  и  т.  д.

Рисунок  1.  Окно  программы  для  ввода  исходных  данных

Рисунок  2.  Графическое  представление  результата  поиска  маршрута  1-2

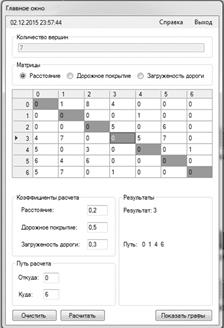
Рисунок  3.  Окно  программы  для  ввода  исходных  данных

Рисунок  4.  Графическое  представление  результата  поиска  маршрута  0-6

Подход  к  оптимизации  прокладки  маршрутов  с  учетом  смешанного  критерия  эффективности  можно  обобщить  на  такие  задачи  как  прокладка  электрических,  канализационных,  локальных  вычислительных  сетей  и  т.  д.

Список  литературы:

1. Автоматическая  трассировка  маршрутов  на  электронной  карте  [Электронный  ресурс]  –  Режим  доступа  –  URL:  http://www.pocketgis.biz  (дата  обращения  19.12.2015). 
2. Алексеев  В.Е.,  Таланов  В.А.  Графы.  Модели  вычислений.  Структуры  данных:  учеб.  пособие.  Нижний  Новгород:  Издательство  Нижегородского  университета,  2005.  –  307  с.
3. Mapquest  route  planner  [Электронный  ресурс]  –  Режим  доступа.  –  URL:  http://www..com/routeplanner:Find  the  shortest  path  from  A  to  B  to  Z  (дата  обращения  19.12.2015).