ОСОБЕННОСТИ ПРИМЕНЕНИЯ ИНТЕГРАЛОВ

Интегральное исчисление возникло в связи с решением задач определения  площадей и объёмов. За 2000 лет до н.э. жители Египта и Вавилона уже умели определять приближённо площадь круга и знали правило для вычисления объёма усечённой пирамиды. Теоретическое обоснование правил вычисления площадей и объёмов впервые появились у древних греков. Философ-материалист Демокрит в V веке до н.э. рассматривает тела, как состоящие из большого числа малых частиц. То есть конус представляет собой множество весьма тонких цилиндрических дисков разных радиусов. Огромную роль в истории интегрального исчисления сыграла задача о квадратуре круга (квадратура круга – построение квадрата, площадь которого равна площади данного круга). Точную квадратуру нескольких криволинейных фигур нашёл Гиппократ (середина V века).

Первым известным методом для вычисления интеграла является метод исчерпания Евдокса (примерно 370 до н. э.). Он пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известен. Этот метод был подхвачен и развит Архимедом, использовался для расчета площадей парабол и приближенного расчета площади круга. В своем сочинении «Квадратура параболы» Архимед пользуется методом исчерпывания для вычисления площади сектора пара­болы. Т.е. Архимед впервые составляет суммы, которые в наше время называются интегральными суммами. Первые значимые попытки развития интеграционных методов Архимеда, увенчавшиеся успехом, были предприняты в XVII веке, когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой стороны – всё более интенсивно развивались экономика, техника, естествознание, а там требовались обширные и глубокие методы изучения и вычисления величин.

 При вычислении площади криволинейной трапеции Ньютон и Лейбниц приходят к понятию  первообразной (или примитивной) функции для данной производной функции f(х), где С могло быть любым. Так называемая сегодня  формула Ньютона-Лейбница позволяет сводить довольно сложное вычисление определенных  интегралов, т.е. нахождение пределов интегральных сумм, к сравнительно  простой операции отыскания первообразных. Лейбницу принадлежит символ дифференциала а позже появился и символ интеграла Символ определённого интеграла 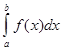 ввёл Ж. Фурье, а термин «интеграл» (от латинского integer - целый) был предложен И. Бернулли.

Работы по исследованию основ дифференциального и интегрального исчислений начинаются в XIX веке трудами О. Коши и Б. Больцано. Тогда же в развитие интегрального исчисления внесли значительный вклад русские учёные-математики М.В. Остроградский, В.Я. Буняковский, В.Я. Чебышев. Это было время, когда современный математический анализ только создавался. Это была, пожалуй, единственная по своей интенсивности эпоха математического творчества, а Эйлер объединил обширный, но разрозненный материал нового анализа в цельную науку.

Со временем, человек приобретал все большую власть над природой, но мечта о полете к звездам оставалась все такой же несбыточной. Писатели-фантасты упоминали ракеты для осуществления космического полета. Однако эти ракеты были технически необоснованной мечтой. Честь открыть людям дорогу к звёздам выпала на долю нашего соотечественника К. Э. Циолковского. Над задачами по созданию искусственного спутника Земли, расчётов траектории выхода их на орбиту работала целая плеяда ученых, во главе с С.П. Королёвым.

Особенно интересны задачи, являющиеся прообразом задач на расчёты траекторий выхода космических аппаратов на заданную орбиту, на нахождение высоты и скорости подъёма или спуска тела и некоторые другие задачи с использованием интегрального исчисления.

Задача 1. Скорость прямолинейного движения тела задана

уравнением . Найти уравнение пути S, если за время t = 2сек тело прошло 20м.

Решение: откудаИнтегрируем: откуда  Используя данные найдём С = 4. Т.е. уравнение движения тела имеет вид  [3, с. 301].

При полете в космос, надо учесть все факторы окружающей нас среды, и чтобы попасть куда нужно, требуется рассчитать траекторию движения, используя исходные данные. Всё это нужно сделать перед тем, как совершится полёт. В 2016 году исполняется 55 лет со дня полёта на орбиту первого космонавта Юрия Алексеевича Гагарина. При расчётах приходилось решать и такие задачи.

Задача 2. Необходимо запустить ракету весом Р = 2·10⁴ Н(Т) с поверхности Земли на высоту h = 1500 км. Вычислить работу необходимую для её запуска.

Решение. f – сила притяжения тела Землёй есть функция от его расстояния х до центра Земли: , где  На поверхности Земли  где сила притяжения равна весу тела Р, а х = R - радиус Земли, поэтому  и  При подъёме ракеты с поверхности Земли на высоту h переменная х изменяется от x = R до x=R+h. Искомую работу находим по формуле: 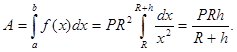 Тогда получаем: работа для запуска ракеты равна  [2, с. 214]

Задача 3. Сила в 10 Н растягивает пружину на 2 см. Какую работу она

совершает при этом?

Решение. По закону Гука, сила F, растягивающая пружину, пропорциональна растяжению пружины, т.е. F = кх. Из условия задачи

к=10/0,02(Н/м), то F = 500х. Работа: 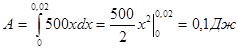 [3, с. 142].

Задача 4. Из шахты глубиной l = 100 м надо поднять равномерно клеть весом Р₁ = 10⁴ Н, которая висит на канате, намотанном на барабан. Вычислить полную работу А_полн, необходимую для поднятия клети, если вес одного погонного метра каната Р₂ = 20 Н.

Решение. Работа по поднятию клети: а по поднятию каната пропорциональна весу каната, т.е. 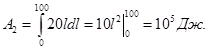 Следовательно, полная работа полна:

 [3, с. 142]

Задача 5. Рессора прогибается под действием силы 1,5·10⁴ Н на 1см. Какую работу надо затратить для деформации рессоры на 3 см? (Деформирующая сила пропорциональна прогибу рессоры.)

Решение. F=кх, где х - прогиб рессоры. При х = 0,01м имеем: . Тогда работа для деформации равна:

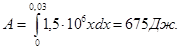 [3, с. 142]

Сложен и небезопасен подъём в космическое пространство, но не менее трудностей таит возвращение на Землю, когда аппарат космического корабля должен приземлиться со скоростью не более 2 м/с. Только в этом случае аппарат, приборы в нём, а главное, члены экипажа, не испытают резкого жёсткого удара. Константин Эдуардович Циолковский решил использовать торможение космического корабля воздушной оболочкой Земли. Двигаясь со скоростью 8 м/с, космический аппарат не падает на Землю. Первая стадия спуска - включение на короткое время тормозного двигателя. Скорость уменьшается на 0,2 км/с, и сразу начинается спуск. Рассмотрим пример решения задачи на составление закона движения при заданных условиях.

Задача 6. Найти закон движения свободно падающего тела при постоянном ускорении g, если в момент движения тело находилось в покое.

Решение: Известно, что ускорение  прямолинейно движущегося тела есть вторая производная пути S по времени t, или производная от скорости  по времени t: , но , следовательно, , откуда . Интегрируем: , и  Из условия: , откуда найдём  и скорость движения: . Найдём закон движения тела: , или . Интегрируем: , . По начальным условиям: , откуда найдём  Имеем уравнение движения падающего тела: - это знакомая формула физики [3, с. 302].

Задача 7. Тело брошено вертикально вверх с начальной скоростью

Найти уравнение движения этого тела (сопротивлением воздуха пренебречь).

Решение: Примем: направление по вертикали вверх - за положительное, а ускорение силы тяжести, как направленное вниз, - за отрицательное. Имеем: , откуда . Интегрируем: то . Т.к. и то С₁:  и  Уравнение скорости:  Находим закон движения тела: т.к.  и  тогда откуда . Интегрируем: или  При  и  найдём , и  Имеем уравнение движения тела:  или  [3, с. 303].

Следующий пример показывает расчет траектории сброса отработанных секций, ненужных приборов, материалов. В этом случае их отправляют на Землю, рассчитав орбиту так, чтобы при прохождении через атмосферные слои они сгорели, а несгоревшие остатки упали на Землю (чаще всего - в океан), не причинив при этом вред.

Задача 8. Составить уравнение кривой, проходящей через точку М (2; -3) и имеющую касательную с угловым коэффициентом .

Решение: В условии задачи дано:  или  Интегрируя, имеем:  При х = 2 и у = -3, С = - 5, а траектория движения имеет вид:  [3, с 300].

Строителям иногда приходится решать задачи по вычислению площадей необычных фигур, для которых нет общеизвестных формул. В этом случае снова выручают интегралы.

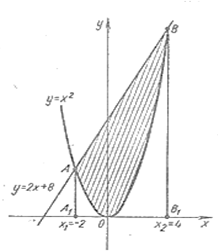Задача 9. Вычислить площадь фигуры, ограниченной линиями:  и

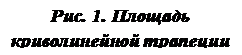Решение: Выполним построение чертежа (рис. 1), для чего решим систему уравнений. Найдём точки пересечения линий: А(-2;4) и В(4;16). Искомая площадь представляет собой разность площадей с пределами интегрирования, а = х₁ = -2 и в = х₂ = 4. Тогда имеем площадь:

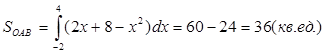 [3, с. 361].

Космонавты и ученые, работая на орбитальной станции, для чистоты эксперимента решают и исследуют многие вопросы астрономии, физики, химии, медицины, биологии и т.д. Сопроводим следующую задачу литературным примером. В известном фантастическом романе Герберта Уэллса «Война миров» описывается нападение марсиан на планету Земля, которые решили расширить свои перенаселённые территории за счёт захвата наших, т.к. климатические условия Земли были подходящими. Начался захват территории и уничтожение землян, которые получили помощь оттуда, откуда совсем не ожидали. Наши «родные» бактерии, с которыми мы уже научились бороться, попав в организм марсиан с воздухом, пищей, водой, нашли в нём благоприятную среду для своего развития и размножения, быстренько адаптировались и, уничтожив марсиан, избавили Землю от захватчиков. Рассмотрим решение задачи,  дающей понятие об этом.

Задача 10. Скорость размножения некоторых бактерий пропорциональна количеству бактерий, имеющихся в наличии в рассматриваемый момент времени t. Количество бактерий утроилось в течение 5ч. Найти зависимость количества бактерий от времени.

Решение: Пусть x(t) есть количество бактерий в момент времени t, а в начальный момент  тогда скорость их размножения. По условию имеем: или   след.: Найдём С: и функция  Известно, чтот.е. или откуда коэффициент пропорциональности равен:  а функция имеет вид:  [1, с. 224].

В знаменитом романе А.Н. Толстого «Гиперболоид инженера Гарина» хотелось бы почувствовать, ощутить, что же это такое – гиперболоид? Какие у него размеры, форма, поверхность, объём? Следующая задача – об этом.

Задача 11. Гипербола  , ограниченная линиями: у = 0, х = a, х = 2а вращается вокруг оси ОХ. Найти объём полученного гиперболоида (рис.2).

Решение. Используем формулу для вычисления объёма тел вращения вокруг оси ОХ с помощью определённого интеграла: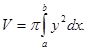  

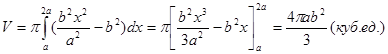[3, с. 367]

Учёные-уфологи занимаются изучением фактов, которые приводят «очевидцы», рассказывая о том, что видели летящий космический корабль в виде огромного светящегося диска («тарелки»), примерно такой формы как на рисунке 3. Рассмотрим решение задачи по определению объёма такой «тарелки».

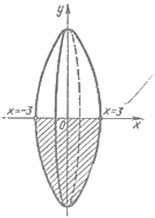
Задача 12. Вычислить объём тела, образованного вращением вокруг оси ОХ площади, ограниченной линиями у = х²- 9 и у = 0.

Решение: При выполнении чертежа параболоида (рис.3) имеем пределы интегрирования от х = -3 до х = 3. Заменим пределы интегрирования в силу симметричности фигуры относительно оси ОУ на х = 0 и х = 3, а результат удвоим. Следовательно, объём диска равен:

   [3, с. 364]

Экономический смысл определённого интеграла выражает объём произведённой продукции при известной функции f(t) - производительности труда в момент t. Тогда объём выпускаемой продукции за промежуток  вычисляется по формуле   Рассмотрим пример для предприятия.

Задача 13. Найти объём продукции, произведённой за 4 года, если функция Кобба-Дугласа имеет вид

Решение. Объём произведённой предприятием продукции равен:

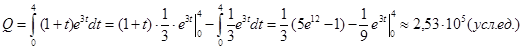 [4, с. 317]

Подводя итоги можно сделать вывод, что применение интеграла раскрывает большие возможности. При изучении геометрии рассматривают вычисление площадей плоских фигур ограниченных отрезками прямых (треугольников, параллелограммов, трапеций, многоугольников), и объёмов тел, полученных при их вращении. Определённый интеграл позволяет вычислять площади сложных фигур, ограниченных любыми кривыми линиями, а также находить объёмы тел, получаемых при вращении криволинейных трапеций вокруг любой оси.

Также хочется отметить, что применение определенного интеграла не ограничивается только вычислением различных геометрических величин, но используется и при решении задач из различных областей физики, аэродинамики, астрономии, химии и медицины, космонавтики, а также, экономических задач.

Список литературы:

1. Апанасов, П.Т. Сборник задач по математике: учеб. пособие/ П.Т. Апанасов, М.И. Орлов. - М.: Высшая школа, 1987.- 303 с.
2. Беденко, Н.К. Уроки по алгебре и началам анализа: методическое пособие/ Н.К. Беденко, Л.О. Денищева. - М.: Высшая школа, 1988. - 239 с.
3. Богомолов, Н.В. Практические занятия по высшей математике: учеб. пособие/ Н.В. Богомолов. - М.: Высшая школа, 1973.- 348 с.
4. Высшая математика для экономистов: учебник/ под ред. Н.Ш. Кремера. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2008.- 479 с.
5. Запорожец, Г.И. Руководство к решению задач по математическому анализу: учеб. пособие/ Г.И. Запорожец.- М.: Высшая школа, 1966. – 460 с.