О ПОЛНОТЕ СИСТЕМЫ ПРОСТЫХ ДРОБЕЙ В ВЕСОВЫХ ПРОСТРАНСТВАХ АНАЛИТИЧЕСКИХ В КРУГЕ ФУНКЦИЙ

В комплексном и гармоническом анализе одним из центральных направлений является представление заданных функций, принадлежащих тому или иному кассу (например,  или ) на заданном множестве в виде простых дробей с фиксированными полюсами. Эта тематика взяла свое начало в работах К. Вейерштрасса о приближениях непрерывных функций на отрезке посредством алгебраических многочленов, Н. И. Ахиезера, Дж. Л. Уолша по представлению произвольных функций из класса  на окружности или класса Харди в виде простых дробей полюсами из внешности единичного круга.

Этому направлению принадлежит данная работа: о представлении аналитических функций в весомом пространстве в виде простых дробей, полюса которых находятся на единичной окружности.

Для изложения основных результатов работы введем следующие обозначения.

Пусть  – комплексная плоскость,  единичный круг на комплексной плоскости,  – единичная окружность . Обозначим через  множество всех аналитических функций в .

Предположим, что  – некоторое замкнутое множество на единичной окружности .

Обозначим через  множество всех простых дробей вида

                          (1)

Напомним, что  – множество всех неотрицательных целых чисел.

Положим также

Символом  обозначим следующее пространство аналитических в   функций,

                    (2)

Основной результат работы – получить полное описание тех замкнутых множеств  на окружности , для которых система функций

                                (3)

составляет всюду плотное множество в пространстве  и соответственно в , где

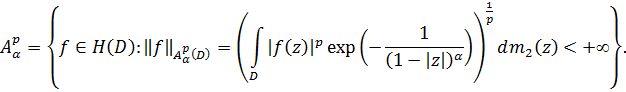
Ясно, что при   является нормированное пространство, а при   – метрическое пространство относительно соответствующей метрики.

Отметим, что задачи такого рода для дискретных множеств в  ранее рассматривались в классических работах Дж. Л. Уолша [4], Н. И. Ахиезера [1], Г. Ц. Тумаркина [3] и других математиков. Подобные задачи в пространстве  и  исследуются впервые.

Сформулируем основные результаты работы в виде следующих двух теорем.

Теорема 1. Пусть  – замкнутое множество на единичной окружности ,  – дополнительные интервалы множества

Тогда если

,                                          (4)

то

                                                 (5)

где замыкание берется в топологии пространства .

В случае пространства  справедливо следующее утверждение

Теорема 2. Пусть ,  – множество из теоремы 1,  определяется равенством (3).

Тогда если дополнительные интервалы множества  удовлетворяют условию (4), то

                                            (6)

при всех , ; где замыкание  берется в топологии пространства .

Замечание. Можно доказать, что если ряд (4) сходится, то указанная система вообще говоря не является полной в пространстве , то есть равенство (5) не выполняется.

Доказательство основано на следующих вспомогательных результатах

Лемма 1. Пусть  - линейный непрерывный функционал на ,

                                          (7)

Предположим, что

                                            (8)

Тогда , причем справедливо следующее равенство

                                (9)

где .

Лемма 2. Пусть  - линейный непрерывный функционал на , и  определяются по формулам (5) и (7).

Тогда справедлива оценка

                              (10)

где  – некоторое положительное число зависящее только от .

Лемма 3. Пусть  – функция, построенная по равенству (8),  – некоторое замкнутое множество на .

Тогда если  и при этом дополнительные интервалы  множества  удовлетворяют условию

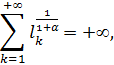
то функция  равна нулю тождественно, т. е. .

Лемма 4. Пусть  – линейный непрерывный функционал на ,  и  – функции, построенные в лемме 1.

Тогда справедливо следующее представление

                   (11)

для произвольной .

В заключение приведем схему доказательства теоремы 1.

Пусть  – произвольный линейный функционал на , ортогональный подпространству , то есть

                  (12)

Положим

Нетрудно видеть, что из (12) следует

Применяя теперь теорему единственности для функций, удовлетворяющих условию (10) получим, что

Далее учтем результат леммы 4 и получим, что

Используя теорему Хана-Банаха получим равенство (5).

Таким образом, теорема доказана.

Доказательство теоремы 2 проводится по схеме, аналогичной схеме доказательства теоремы 1.

Список литературы:

1. Ахиезер Н. И. Лекции по теории аппроксимации. 2-е издание. М.: Наука, 1965.
2. Мандельбройт С. Квазианалитические классы функций. ОНТИ НКТП СССР, 1937.
3. Тумаркин Г. Ц. Приближения в различных метриках функций, заданных на окружности, последовательностями рациональных дробей с фиксированными полюсами. // Изв. АН СССР. – Сер. матем. – 1966. – т. 30 – выпуск 4, 721–766 с.
4. Уолш Дж. Л. Интерполяция и аппроксимация рациональными функциями в комплексной плоскости // М: Изд. ин. литературы, 1961. – 508 с.
5. Koosis P. The logarithmic integral I. Cambridge: University Press, 1988 (1998).