ПРОГРАММНОЕ  РЕШЕНИЕ  ЗАДАЧИ  О  ВЕРШИННОМ  ПОКРЫТИИ  С  ПОМОЩЬЮ  ПРИБЛИЖЕННЫХ  АЛГОРИТМОВ

Абрамов  Андрей  Викторович

студент  3  курса,  кафедра  геоинформатики  и  информационной  безопасности,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Е-mail: 

Максимов  Алексей  Игоревич

студент  3  курса,  кафедра  геоинформатики  и  информационной  безопасности,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Е-mail: 

Тишин  Владимир  Викторович

научный  руководитель,  доцент,  кафедра  прикладной  математики,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Введение

Задача  о  нахождении  наименьшего  вершинного  покрытия  графа  на  сегодняшний  день  является  крайне  актуальной,  можно  даже  заявить,  что  она  находится  на  переднем  крае  науки,  так  как  точного  алгоритма  нахождения  вершинный  покрытий  до  сих  пор  не  разработано.  Вершинные  покрытия  находят  широкое  практическое  применение  —  от  размещения  военных  гарнизонов  по  населенным  пунктам  до  выбора  книг  для  прочтения  из  серии.

С  точки  зрения  информатики,  эта  задача  является  NP-полной,  это  значит,  что  решить  эту  задачу  можно  за  время,  зависящее  полиномиально  от  числа  входных  данных.  Полнота  же  задачи  означает,  что  к  ней  можно  сводить  другие  полиномиальные  задачи  за  конечное  число  операций.  Таким  образом,  задача  нахождения  наименьшего  вершинного  покрытия  является  «типовой»  задачей,  разрешив  которую,  мы  автоматически  решаем  широкий  класс  задач,  которые  можно  к  ней  свести.

Цель  нашей  исследовательской  работы  —  реализовать  программу,  способную  строить  минимальные  вершинные  покрытия  графов.

Для  ее  достижения  были  поставлены  следующие  задачи:

1.  Изучить  алгоритмы  решения  задачи  о  наименьшем  вершинном  покрытии,

2.  Использовать  выбранные  алгоритмы  при  создании  программы.

Основные  понятия

На  всякий  случай  напомним  основные  понятия,  которые  фигурируют  в  нашей  исследовательской  работе.  Граф  —  пара  множеств  (V,E),  где  V  —  множество  вершин,  E  —  множество  ребер,  представляющее  собой  пару  элементов  множества  V.  Если  пары  множества  E  упорядочены,  то  граф  называется  ориентированным  (направленным),  если  нет,  то  неориентированным  (ненаправленным).  В  нашей  работе  мы  рассмотрим  неориентированные  графы,  хотя  программа,  ставшая  результатом  нашей  работы,  может  работать  как  с  направленными,  так  и  с  ненаправленными  графами.

Граф  называется  взвешенным,  если  его  ребрам  приписаны  некоторые  числа  —  веса.  Веса  можно  интерпретировать  по-разному,  например,  как  расстояние  между  населенными  пунктами,  время  проезда  от  одного  пункта  к  другому,  стоимость  проезда  между  остановками  и  т.  д.  Граф  часто  изображается  в  виде  диаграмм,  где  вершины  изображаются  точками,  а  ребра  —  линиями,  соединяющими  вершины.

Граф  можно  задать  в  виде  матрицы  весов  –  квадратной  матрицы,  каждый  столбец  и  строка  которой  соответствуют  вершине  графа,  а  элементами  являются  веса  ребер  между  данными  вершинами.  Именно  в  таком  виде  граф  задается  для  нашей  программы.

Вершина  покрывает  ребро  (или  ребро  покрывает  вершину),  если  они  инцидентны.

Покрывающее  множество  вершин  –  множество  вершин,  покрывающее,  все  ребра  графа  (аналогично  определяется  покрывающее  множество  ребер).

Минимальное  покрывающее  множество  вершин  —  такое  покрывающее  множество  вершин,  что  удаление  одной  вершины  из  него  приводит  к  тому,  что  оно  перестает  быть  покрывающим.

Наименьшее  покрывающее  множество  вершин  —  минимальное  покрывающее  множество  с  минимальным  числом  элементов  из  возможных.  Число  элементов  в  этом  множестве  —  число  вершинного  покрытия.

Формулировка  задачи  о  вершинном  покрытии

Теперь  строго  сформулируем  задачу,  решению  которой  мы  посвятили  свою  работу.

Задача  нахождения  вершинного  покрытия  графа  —  нахождение  наименьшего  покрывающего  множества  вершин  графа.

Приближенные  алгоритмы  нахождения  решения

Точного  алгоритмического  решения  выбранной  нами  задачи  на  сегодняшний  день  не  существует,  есть  только  алгоритмы,  дающие  приближенный  ответ  с  определенной  погрешностью.  Такая  ситуация  является  вполне  типичной  для  NP-полных  задач.  Однако  стоит  отметить,  что  сегодня  активно  разрабатываются  новые  и  все  более  точные  приближенные  алгоритмы  для  вершинных  покрытий.  Поскольку  они  приближенные,  то  ни  один  из  них  не  может  гарантировать,  что  найденное  покрытие  будет  наименьшим  или  хотя  бы  минимальным.

Рассмотрим  два  наипростейших  приближенных  алгоритма  с  «говорящими»  именами,  которые  мы  будем  использовать  при  реализации  программы.

«Ленивый»  алгоритм

Этот  алгоритм  предельно  прост,  как  в  реализации,  так  и  в  понимании  —  мы  просто  берем  любое  ребро  наугад  и  добавляем  в  покрытие  одну  из  инцидентных  ему  вершин,  совершенно  не  задумываясь  о  ее  степени.

«Ленивый»  алгоритм  для  вершинного  покрытия  заключается  в  следующем:

На  каждом  шаге,  пока  не  кончатся  все  ребра  в  графе:

1.  Выбираем  случайное  ребро  графа 

2.  Добавляем  в  решение    одну  из  выбранных  вершин    или  .

3.  Удаляем  из  графа  все  ребра,  инцидентные  вершинам    или  .

Алгоритм  ошибается  не  более  чем  в  2  раза,  за  «лень»  приходится  дорого  заплатить,  однако  для  небольших  графов  этот  алгоритм  вполне  актуален.

«Жадный»  алгоритм

Название  этого  алгоритма  говорит  само  за  себя,  его  идея  состоит  в  добавлении  в  покрытие  в  первую  очередь  вершин  с  наибольшей  степенью,  ведь  они  покрывают  большее  число  ребер.

Алгоритмически  это  выглядит  так:

На  каждом  шаге,  пока  не  кончатся  все  ребра  в  графе:

1.  Выбираем  вершину,  покрывающую  наибольшее  число  ребер

2.  Добавляем  ее  в  решение 

3.  Удаляем  ее  из  графа  и  все  ребра,  ей  инцидентные

Алгоритм  ошибается  не  более  чем  в  1  +  ln  m  раз  (m  —  число  вершин  наименьшего  покрытия).  Кажется,  что  ошибка  этого  алгоритма  еще  больше,  чем  у  предыдущего,  да  еще  и  растет  с  ростом  числа  вершин,  однако  этот  рост  логарифмический,  значит  не  очень  резкий.  На  небольших  графах  алгоритм  с  большой  вероятностью  дает  верное  значение  покрытия.

Решение  задачи  вершинного  покрытия

Результатом  нашей  работы  стала  программа,  способная  находить  наименьшие  вершинные  покрытия  обоими  из  рассмотренных  алгоритмов  —  и  «жадным»,  и  «ленивым».  Она  способна  работать  как  с  ориентированными,  так  и  с  неориентированными,  как  с  взвешенными,  так  и  невзвешенными  графами.  Так  же  программный  продукт  способен  визуализировать  граф  в  виде  диаграммы.

Скажем  несколько  слов  о  том,  что  из  себя  представляет  наш  программнй  продукт.  Программа  написана  на  Qt  5  —  самой  последней  реализации  кроссплатформенного  фреймворка,  возможна  компиляция  под  все  существующие  платформы.  Фреймворк  дополняет  язык  С++  для  более  удобного  программирования.  Программа  создана  с  учётом  последующей  возможности  перевода  интерфейса.  Используется  динамически  выделяемое  пространство  памяти  под  реализацию  сцены  (отрисовки  графических  объектов)  так  что  перегрузить  программу  трудно,  а  при  минимальном  количестве  узлов  —  расходуется  минимальное  количество  необходимой  памяти.  Интерфейс  понятен  и  с  пояснениями.  Так  же  программа  собрана  со  статической  линковкой  DLL  файлов,  что  позволяет  использовать  её  без  предварительной  установки  (не  оставляет  никаких  следов  в  системе).

В  качестве  наглядного  и  актуального  примера  мы  решили  решить  следующую  практическую  задачу  —  разместить  военные  гарнизоны  по  Центральному  военному  округу  РФ  так,  чтобы  они  контролировали  все  дороги  между  населенными  пунктами,  причем  в  наименьшем  числе  городов,  чтобы  не  распылять  военные  ресурсы.  Вершинами  графа  в  контексте  нашей  задачи  будут  населенные  пункты,  а  ребрами  —  соединяющие  их  дороги.  Получился  ненаправленный  граф  на  38  вершинах.

Рисунок  1.  Граф  на  основе  карты

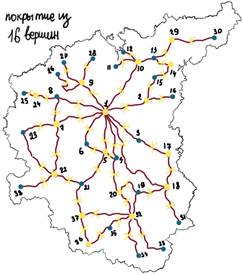
Рисунок  2.  Решение  задачи  без  программы

При  решении  задачи  собственными  силами  в  покрывающем  множестве  оказалось  16  вершин.  Теперь  посмотрим,  как  с  этой  задачей  справится  наша  программа.  Заполним  матрицу  смежности  графа  и  визуализируем  его.

Рисунок  3.  Программная  визуализация  графа

Запустим  алгоритмы  и  проанализируем  результаты  их  работы.

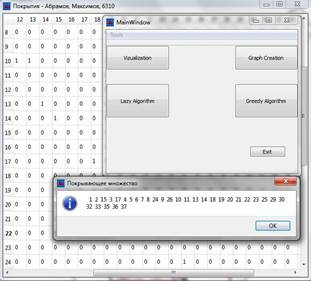
Рисунок  4.  Результат  «ленивого»  алгоритма

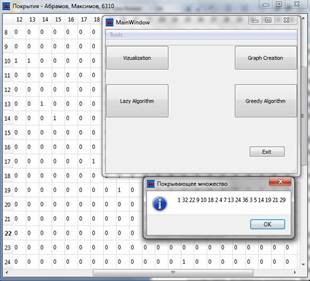
Рисунок  5.  Результат  «жадного»  алгоритма

«Ленивый»  алгоритм  выдал  нам  список  из  31  вершины,  с  одной  сторон,  результат  не  очень  впечатляет,  однако,  как  мы  выяснили,  алгоритм  может  выдать  покрывающее  множество  в  два  раза  больше  наименьшего,  так  что  результат  его  работы  вполне  согласуется  с  теорией.  «Жадный»  алгоритм  показал  себя  гораздо  лучше,  выдав  18  вершин.  Ошибка  составила  всего  2  вершины.

Заключение

Теория  графов  как  научная  дисциплина  крайне  интересна  широтой  практических  задач,  которые  возможно  решить  с  ее  применением.  Эту  работу  мы  посвятили  одной  задаче  этой  теории  —  нахождению  наименьшего  вершинного  покрытия.  В  рамках  этой  задачи  был  решен  сугубо  практический  вопрос  —  как  разместить  вооруженные  силы  в  военном  округе.

Задачи,  которые  мы  поставили  на  пути  к  достижению  поставленной  цели,  были  выполнены  —  изучены  два  алгоритма  нахождения  покрытий,  оба  они  реализованы  в  программном  виде.  Так  же  достигнута  наша  основная  цель  —  программа  для  нахождения  вершинных  покрытий  успешно  реализована.

Однако  мы  не  намерены  останавливаться  на  достигнутом,  ведь  задача  о  точном  алгоритмическом  нахождении  наименьшего  вершинного  покрытия  графа  остается  открытой.

Список  литературы:

1.Додонова  Н.Л.  Конспект  лекций  по  дисциплине  теория  конечных  графов  и  ее  применения  Самара:  2010  —  с.  52.

2.Свами  М.,  Тхуласираман  К.  Графы,  сети  и  алгоритмы.  М.:  Мир,  1984,  —  454  с.

3.Жадные  алгоритмы  в  задачах  о  покрытии  Н.Н.  Кузюрин  С.А.  Фомин  [Электронный  ресурс]  —  режим  доступа.  —  URL:  http://discopal.custis.ru/images/archive/8/82/20101202232637!Greedy-covering.beam.pdf  (дата  обращения  10.04.2015).