ПРИЛОЖЕНИЕ  ТЕОРИИ  ГРАФОВ  К  РЕШЕНИЮ  ЗАДАЧИ  ТОПОЛОГИЧЕСКИХ  ПЕТЕЛЬ  В  СЕТЯХ  ETHERNET

Князев  Денис  Михайлович

студент  3  курса,  факультет  информатики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

E   -mail:  knyazevdenis.gm@gmail.ru

Грибанов  Иван  Алексеевич

студент  3  курса,  факультет  информатики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

E  -mail: 

Тишин  Владимир  Викторович

научный  руководитель,  доцент,  кафедра  прикладной  математики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

Введение

В  работе  рассматривается  приложение  теории  графов,  для  решения  задачи  маршрутизации  в  локальных  вычислительных  сетях  Ethernet  методом  связующего  дерева.  Данный  механизм  позволяет  исключить  повторную  передачу  кадров  (фреймов)  в  локальной  вычислительной  сети  Ethernet  по  причине  наличия  в  последней  топологических  петель,  а  также  решает  задачу  резервирования,  используя  механизмы  введения  избыточности.

Если  для  обеспечения  избыточности  между  коммутаторами  создается  несколько  соединений,  то  могут  возникать  коммутационные  петли.  Петля  предполагает  существование  нескольких  маршрутов  по  промежуточным  сетям,  а  сеть  с  несколькими  маршрутами  между  источником  и  приемником  отличается  повышенной  отказоустойчивостью.  Хотя  наличие  избыточных  каналов  связи  очень  полезно,  петли,  тем  не  менее,  создают  проблемы,  которые  могут  привести  к  отказу  сети  [2].

Spanning  Tree  Protocol

Проблема  топологических  петель  в  сети  Ethernet  была  решена  в  IEEE  Committees  802  в  стандарте  802.1D  с  помощью  технологии,  известной  как  Spanning  Tree  Protocol  (STP).  STP,  основанный  на  теории  графов,  преобразует  циклические  структуры  в  топологию  дерева,  отключая  избыточные  связи.  Такой  подход  гарантирует  единственность  пути  из  любого  узла  в  локальной  сети  к  любому  другому  [3].  Неактивные  узлы  переводятся  в  режим  ожидания,  пока  не  произойдет  сбой  в  работе  сети.  В  таких  ситуациях  STP  будет  пытаться  построить  новое  дерево,  используя  любое  из  ранее  не  активных  соединение  [2].

Чтобы  проиллюстрировать  работу  STP,  мы  должны  сначала  ознакомиться  с  различиями  между  физической  и  логической  топологиями  сетей.  Кроме  того,  существует  ряд  терминов,  связанных  с  алгоритмом  связующего  дерева,  которые  определены  в  стандарте  и  с  которыми  мы  должны  познакомиться.  Таким  образом,  мы  получим  знания,  необходимые  для  понимания  работы  алгоритма.

Физическая  и  логическая  топологии

Технология  прозрачных  мостов  (transparent  bridges)  предоставляет  четкое  различие  физической  и  логической  топологий  мостовых  локальных  сетей.  Это  различие  позволяет  создавать  топологии  сетей,  в  которых  неактивные,  но  физически  существующие  маршруты  могут  быть  введены  в  эксплуатацию,  если  основной  маршрут  выйдет  из  строя.  Кроме  того,  неактивные  и  активные  маршруты  на  физическом  уровне  формируют  петлю,  нарушающую  работу  сети  в  случае,  если  оба  маршрута  были  активными  одновременно,  но  на  логическом  петля  не  образуется.

Верхняя  часть  рисунка  1  иллюстрирует  одну  из  возможных  физических  топологий  мостовых  сетей.  Стоимость  (C),  присвоенная  каждому  соединению,  будет  обсуждаться  позже.  В  нижней  части  рисунка  1  проиллюстрирована  возможная  логическая  топология  физической  конфигурации,  показанной  в  верхней  части  этой  иллюстрации.

В  процессе  построения  логического  пути,  мост  (коммутатор)  будет  пересылать  кадры,  необходимые  для  формирования  цепочек  активных  мостов.  В  этом  случае  говорят,  что  такие  порты  коммутатора,  через  которые  передаются  кадры,  находятся  в  состоянии  пересылки  кадров.  Пересылка  кадров  через  порты,  функционирование  которых  ведет  к  образованию  петель,  запрещена.  Такие  порты  называют  неназначенными.

После  завершения  работы  протокола,  порт  из  неактивного  состояния  может  быть  переведен  в  активное,  а  проходящий  через  него  путь  становится  частью  логической  топологии  сети.  Этот  новый  путь,  как  правило,  образуется  после  отказа  соединения,  составляющего  часть  уже  сформированной  логической  сети,  или  реконфигурации  взаимосвязанных  сетей  и  не  должен  образовывать  замкнутый  контур.

Spanning  Tree  Algorithm

Основанием  для  алгоритма  связующего  дерева  является  древовидная  структура.  Обосновано  это  тем,  что  дерево  как  структура  не  имеет  связей,  образующих  петли.  Термин  «связующий»  используется  в  силу  того,  что  ветви  дерева  охватывают  все  подсети  исходной  сети.

Рассмотрим  концепцию,  лежащую  в  основе  остовных  деревьев.  Для  получения  дерева,  мы  должны  выбрать  точку  отсчета.  В  качестве  примера  возьмем  граф,  показанный  на  рисунке  2.  Остовным  деревом  графа  называется  связный  ациклический  подграф,  который  соединяет  все  узлы  [1].  Рассматриваемый  граф  имеет  восемь  различных  каркасов.  Все  они  проиллюстрированы  в  нижней  части  рисунка  2.

Минимальное  связующее  дерево

Предположим,  что  связи,  соединяющие  каждый  узел  сети  имеют  назначенную  длину  или  вес.  Тогда  вес  дерева  определим  как  сумму  весов  его  связей  или  ребер.  Если  суммы  весов  ребер  остовных  деревьев  отличаются,  то  такие  древовидные  структуры  будут  иметь  разный  вес.  Таким  образом,  определение  минимального  охватывающего  дерева  требует,  чтобы  мы  рассмотрели  каждое  из  остовных  деревьев,  покрывающих  граф  и  определили  структуру,  которая  будет  имеет  минимальную  длину  или  вес.

Нахождение  минимального  связующего  дерева  может  быть  достигнуто  путем  перечисления  всех  связующих  деревьев,  дальнейшим  подсчетом  веса  каждого  из  них  и  выбором  остова,  имеющего  минимальный  вес.  Это  способ,  который  всегда  работает,  но,  к  сожалению,  не  обладает  сколь  либо  приемлемой  эффективностью,  особенно  когда  исходный  граф  разрастается  и  содержит  значительное  количество  остовных  деревьев.  Гораздо  надежнее  метод,  полученный  с  использованием  соответствующего  алгоритма.

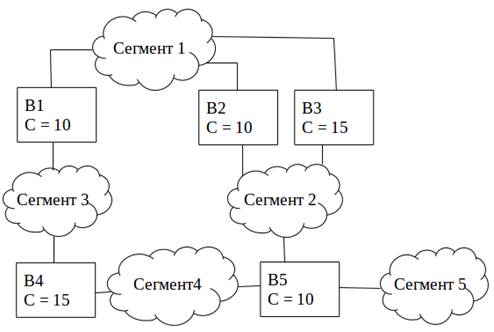
(а)  Физическая  топология

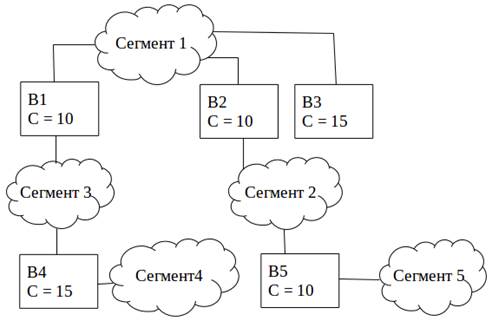
(б)  Логическая  топология

Рисунок  1.  Физическая  и  логическая  топологии  сети

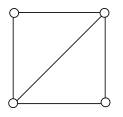  (а)  Исходный  граф

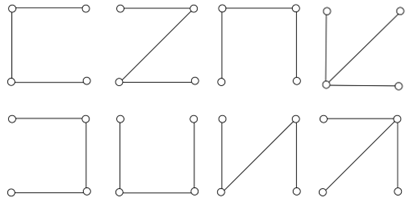  (б)  Остовные  дерева

Рисунок  2.  Варианты  остовных  деревьев  графа

Алгоритм  Крускала

Есть  несколько  популярных  алгоритмов,  разработанных  для  решения  задачи  поиска  минимального  остовного  дерева  графа.  Одним  из  таких  алгоритмов  является  алгоритм  Крускала,  который  относительно  легок  в  понимании  и  будет  использоваться  для  иллюстрации  нахождения  минимального  связующего  дерева.  Поскольку  нам  нужны  веса  или  длины,  присвоенные  каждому  ребру  графа  или  соединению  в  сети,  давайте  рассмотрим  пример,  ранее  показанный  на  рисунке  2,  и  укажем  некоторые  веса.  Рисунок  3  иллюстрирует  полученный  взвешенный  граф.

Алгоритм  Крускала  формулируется  следующим  образом  [1]:

1.  В  начале  множество  ребер  графа  (G)  сортируется  в  порядке  возрастания  весов.

2.  Далее  формируется  подграф  S  графа  G.  В  начальном  состоянии  он  пуст.

3.  Из  всех  рёбер,  не  входящих  в  S  и  добавление  которых  в  S  не  вызовет  появление  в  нём  петель,  выбирается  ребро  минимального  веса  и  добавляется  к  S.

4.  Алгоритм  завершил  работу,  если  в  S  включены  все  вершины  графа.

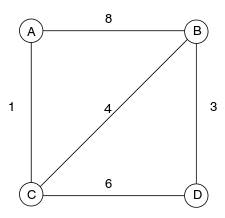
Рисунок  3.  Взвешенный  граф

Применим  алгоритм  Крускала  к  графу,  показанному  на  рисунке  3.

1.  Отсортируем  ребра  графа  по  возрастанию  веса  и  получим  такую  таблицу:

2.  Сформируем  пустой  подграф  S  графа  G. 

3.  Теперь  будем  последовательно  добавлять  каждое  ребро  в  S  при  условии,  что  такая  операция  не  будет  образовывать  цикл.

Таким  образом,  на  первом  шаге  в  S  добавляется  A-C:

,  S  =  {(A,  C)}.

На  втором  —  B-D:

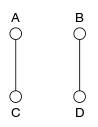,  S={(A,  C),  (B,  D)}.

На  третьем  —  C-B:

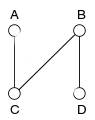,  S={(A,  C),  (B,  D),  (C,  B)}.

Обратите  внимание,  что  мы  не  можем  продолжать,  так  как  добавление  ребер  C-D  и  A-B  будет  образовывать  цикл.  Применив  алгоритм,  мы  получили  минимальное  остовное  дерево,  состоящее  из  ребер  (A,  B),  (B,  D),  (C,  B)  и  имеющее  вес  1  +  4  +  3,  или  8.  Теперь,  когда  мы  знаем  прекрасный  способ  поиска  минимального  остовного  дерева,  обратим  наше  внимание  на  применимость  этого  способа  к  сетевым  технологиям.

Как  и  корень  у  дерева,  один  мост  в  остове  сети  будет  иметь  уникальный  статус.  Известный  как  корневой,  этот  мост  назначается  «центром»  связующего  дерева  и,  благодаря  такому  расположению,  осуществляет  передачу  наибольшего  количества  внутрисетевого  трафика.

Так  как  мосты  и  порты  мостов  могут  быть  как  активным,  так  и  неактивными,  необходим  механизм  для  определения  моста  и  его  портов.  Каждому  мосту  в  сети  покрывающего  дерева  присваивается  уникальный  идентификатор  моста.  Этот  идентификатор  складывается  из  двух  частей:  два  байта,  указывающие  уровень  приоритета  моста,  и  MAC-адрес  его  наименьшего  порта.  Уровень  приоритета  позволяет  задать  порядок,  в  котором  мосты  будут  добавляться  в  логическую  сеть.  Его  особенность  состоит  в  том,  что  лучшим  считается  мост  с  наименьшим  приоритетом.  Аналогично  уровню  приоритета  моста,  каждый  порт  имеет  двухбайтовый  идентификатор.  Таким  образом,  уникальный  идентификатор  моста  и  идентификатор  порта  позволяют  однозначно  определить  каждый  порт  на  мосту.

Стоимость  пути

Алгоритм  связующего  дерева  предполагает  как  различие  в  физической  организации  путей  между  мостами,  так  и  механизм,  обеспечивающий  выбор  одного  из  маршрутов  по  необходимым  признакам.  Такой  механизм  реализуется  путем  назначения  стоимости  пути  для  каждого  соединения  в  исходной  сети.  Мы  имеем  возможность  назначить  низкую  стоимость  пути  на  более  предпочтительный  маршрут  и  высокую  стоимость  маршруту,  который  будет  использоваться  только  в  экстренной  ситуации.  Когда  веса  назначены  всем  соединениям  в  сети,  с  каждым  мостом  будут  связаны  одно  или  несколько  соединений,  имеющих  разные  стоимости.  Эти  стоимости  обусловлены  выбором  различных  маршрутов  к  корневому  мосту.  Одна  из  этих  стоимостей  ниже,  чем  остальные  .  Эта  стоимость  называется  корневой  стоимостью  пути  моста  (root  path  cost),  а  порт,  через  который  обеспечивается  наименьшая  стоимость  пути,  называется  корневым  портом  (root  port).

Назначенные  мосты

Как  было  отмечено  ранее,  алгоритм  связующего  дерева  не  допускает  появления  петель  в  связанной  сети.  Чтобы  этого  достигнуть,  только  один  мост,  связывающий  две  сети,  пересылает  данные  в  любое  определенное  время.  Этот  мост  называется  назначенным  (designated).  В  свою  очередь,  все  другие  мосты,  связывающие  эти  две  сети,  будут  находиться  в  заблокированном  состоянии.

Построение  дерева  охвата

Алгоритм  построения  связующего  дерева  состоит  из  трех  шагов,  которые  позволяют  построить  активную  топологию  сети.  На  первом  шаге  определяется  корневой  мост.  Для  этого  каждый  мост  в  сети  изначально  считает,  что  он  корневой.  Чтобы  определить,  какой  мост  будет  фактически  действовать  как  корневой,  каждый  мост  периодически  передает  специальные  конфигурационные  пакеты  BPDU  (Bridge  Protocol  Data  Unit),  которые  будут  описаны  ниже.  Каждый  BPDU  пакет  передается  на  все  порты  коммутатора.  Структура  BPDU  содержит  в  себе  приоритет  моста,  который  определяется  при  настройке  оборудования.  Мосты  в  сети  периодически  передают  свои  BPDU  пакеты.  Узлы,  получающие  BPDU  с  более  низкой  приоритетной  стоимостью,  чем  его  собственные,  прекращают  передавать  свои  BPDU  кадры,  однако  они  продолжают  транслировать  конфигурационные  пакеты  с  более  низкой  стоимостью.  Таким  образом,  после  некоторого  промежутка  времени,  коммутатор  с  самой  низкой  приоритетной  стоимостью  будет  признан  корневым  мостом.

Рассмотрим  рисунок  1б.  Предположим,  что  мост  B1  был  отобран  как  корневой.  На  следующем  шаге  будет  определена  стоимость  пути  от  каждого  моста  до  корневого,  и  минимальная  стоимость  станет  корневой  стоимостью  пути.  Порт  в  направлении  которого  стоимость  пути  до  корневого  моста  наименьшая,  называется  корневым  портом  коммутатора.  Для  каждого  моста,  кроме  корневого  определяется  такой  порт.  Если  стоимость  пути  будет  одинаковой  для  двух  или  более  мостов,  то  будет  выбран  коммутатор  с  самой  низкой  приоритетной  стоимостью.  Когда  все  маршруты  будут  определены,  активируются  назначенные  порты.

Рассмотрим  рисунок  1a.  На  нем  мы  видим  расставленные  приоритеты  для  каждого  коммутатора.  Предположим,  что  коммутатор  B1  был  отобран  как  корневой.  Ожидается,  что  большая  часть  трафика  будет  передаваться  между  сегментом  1  и  сегментом  3.  Поэтому  коммутатор  B1  станет  назначенным  мостом  между  сегментом  1  и  сегментом  3.  Здесь  термин  «назначенный  мост»  означает  мост,  который  имеет  порт  с  наименьшей  стоимостью  пути  до  корневого  моста.  Назначим  цены  путей  для  каждого  соединения  следующим  образом:  маршруту  через  мост  B2  назначим  стоимость  10,  а  маршруту  через  мост  B3  назначим  стоимость  15.  Таким  образом  коммутатор  B2  между  сегментом  2  и  сегментом  1  становится  назначенным  мостом.  Следовательно,  как  видно  из  рисунка  1б,  соединение  через  мост  B3  становится  неактивным.  Аналогичным  образом  определяем,  что  наименьшая  стоимость  пути  для  соединения  сегмента  5  к  корневому  мосту  достигается,  если  маршрут  проходит  через  сегмент  2  и  сегмент  1.  Таким  образом  коммутатор  B5  становится  назначенным  мостом  для  сегмента  5  и  сегмента  2.

Конфигурационные  сообщения  Bridge  Protocol  Data  Unit.

Как  было  отмечено  ранее,  коммутаторы  получают  информацию  о  топологии  сети  при  помощи  специальных  служебных  сообщений  BPDU.  Как  только  определен  корневой  мост,  он  начинает  распространять  специальные  "HELLO"  пакеты  на  коммутаторы,  с  которыми  связан.  Согласно  протоколу  связующего  дерева,  такие  пакеты  должны  передаваться  каждые  1—10  секунд.  Назначенные  мосты  обновляют  информацию  о  стоимости  пути  и  ретранслируют  сообщения.  Резервный  коммутатор  будет  контролировать  сообщения  BPDU.  Если  назначенный  мост  не  получает  BPDU  пакеты  на  своем  корневом  порту  в  течение  некоторого  промежутка  времени  (20  секунд),  то  предполагается,  произошло  повреждение  соединения  между  назначенным  мостом  и  корневым  или  отказ  устройства.  Если  этот  коммутатор  все  еще  получает  конфигурационные  сообщения  BPDU  на  других  портах,  то  он  назначит  своим  корневым  портом  порт,  который  получает  BPDU  с  наименьшей  стоимостью.

Информация  о  том,  что  резервный  мост  должен  стать  корневым  или  назначенным  содержится  в  "HELLO"  BPDU.  Процесс,  в  результате  которого  мосты  определяют  свою  роль,  повторяющийся.  Когда  в  сети  появляются  новые  коммутаторы,  они  начинают  «прослушивать»  сеть,  получая  информацию  о  топологии.  Аналогично,  когда  какой-либо  коммутатор  удаляют  из  сети,  оставшиеся  мосты  обмениваются  информацией,  чтобы  сформировать  новое  связывающее  дерево.

Выводы

В  нашей  работе  мы  рассмотрели  математическую  основу  технологии  Spanning  Tree  Protocol  и  описали  основные  этапы  ее  функционирования.

Несмотря  на  то,  что  алгоритм  STP  устраняет  двойные  связи,  это  может  быть  недостатком  в  тех  случаях,  когда  такие  связи  между  сетями  желаемы.  Кроме  того,  если  соединение  или  коммутатор  выходят  из  строя,  то  время,  требуемое  для  построения  нового  связующего  дерева,  может  достигать  45—60  секунд.  На  это  время  сеть  перестает  функционировать  и  может  произойти  потеря  передаваемых  данных.

Список  литературы:

1.Белоусов  А.И.,  Ткачев  С.Б.  Дискретная  математика.  М.:  МГТУ,  2006.  —  744  с.  —  ISBN  5-7038-2886-4.

2.Смирнова  Е.В.,  Пролетарский  А.В.,  Баскаков  И.В.,  Федотов  Р.А.  Построение  коммутируемых  компьютерных  сетей:  учебное  пособие  /  Е.В.  Смирнова  и  др.  М.:  Национальный  Открытый  Университет  «ИНТУИТ»:  БИНОМ.  Лаборатория  знаний,  2011.  —  367  с.:  ил.,  табл.  —  (Основы  информационных  технологий).

3.Трегубов  Р.Б.,  Лазарев  С.Н.,  Андреев  С.Ю.  Алгоритм  решения  прикладной  задачи  теории  графов  о  нахождении  k  минимальных  остовных  деревьев  //  Интернет-журнал  «Науковедение»,  —  2014  —  №  5  (24)  М.:  Науковедение,  2014  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://naukovedenie.ru/PDF/102TVN514.pdf,  свободный.  —  Загл.  с  экрана.  —  Яз.  рус.,  англ.  (дата  обращения  25.04.2015).