ПРИМЕНЕНИЕ  ТЕОРИИ  АЛГОРИТМОВ  К  СИТУАЦИЯМ  ИЗ  ПОВСЕДНЕВНОЙ  ЖИЗНИ

Хантова  Анна  Дмитриевна

студент  3  курса,  факультет  информатики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

E -mail:  ad.khantova@yandex.ru

Тишин  Владимир  Викторович

научный  руководитель,  доцент,  кафедра  прикладной  математики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

Введение

Говоря  о  математическом  описании  чего-либо,  мы,  как  правило,  представляем  какой-то  сложный  процесс  или  что-то  абстрактное.  Однако  математический  аппарат  весьма  удачно  применяется  к  ситуациям,  с  которыми  мы  сталкиваемся  ежедневно.  При  помощи  математических  методов  можно  описать  многие  природные  явления:  формулы  закона  всемирного  тяготения  и  закона  Архимеда.  Или,  например,  можно  описать  популяцию  животных  с  помощью  дифференциальных  уравнений.  Так  же  можно  применить  математический  аппарат  и  к  ситуациям  из  повседневной  жизни:  посчитать  с  помощью  аппарата  теории  вероятности,  сколько  в  среднем  нужно  купить  шоколадок,  чтобы  собрать  все  вкладыши,  или  описать  наши  действия  при  помощи  теории  алгоритмов.

Конечно,  жизнь  во  всем  своем  многообразии  слишком  непредсказуема,  чтобы  можно  было  формализовать  все  её  аспекты  и  проработать  модель  поведения  для  любого  случая.  Однако,  многие  действия,  которые  мы  совершаем,  не  задумываясь  о  том,  насколько  они  поддаются  математическому  описанию,  можно  представить  в  виде  алгоритмов.

Цель:  выбрать  несколько  ситуаций  из  повседневной  жизни  и  описать  их  с  помощью  теории  алгоритмов.

Задачи:  изучить  историю  возникновения  теории  алгоритмов,  изучить  способы  формального  определения  понятия  алгоритма,  применить  выбранные  способы  к  ситуациям  из  повседневной  жизни. 

Актуальность:  применение  теории  алгоритмов  к,  казалось  бы,  далёким  от  математики  ситуациям  поможет  лучше  понять  саму  теорию  и  поспособствует  более  широкому  взгляду  на  обыденные  вещи,  прежде  всего,  с  математической  точки  зрения.

История  возникновения  теории  алгоритмов

Первым  дошедшим  до  нас  алгоритмом  в  его  интуитивном  понимании  —  конечной  последовательности  элементарных  действий,  решающих  поставленную  задачу,  считается  так  называемый  алгоритм  Евклида  —  алгоритм  нахождения  наибольшего  общего  делителя  двух  чисел.

Слово  «алгоритм»  возникло  довольно  поздно.  Оно  образовано  от  имени  арабского  математика  аль-Хорезми,  жившего  в  IX  веке  н.  э.  Понятие  «алгоритм»  не  имеет  строго  определенной  формулировки.  Алгоритм  можно  определить  как  набор  инструкций,  следуя  которым  можно  по  входным  данным  определенного  вида  получать  на  выходе  некоторый  результат.

Начало  современной  теории  алгоритмов  положила  работа  немецкого  математика  Курта  Гёделя  1931  года,  в  которой  было  показано,  что  некоторые  математические  проблемы  не  могут  быть  решены  алгоритмами  из  некоторого  класса.  Общность  результата  Геделя  связана  с  тем,  совпадает  ли  использованный  им  класс  алгоритмов  с  классом  всех  (в  интуитивном  смысле)  алгоритмов.  Эта  работа  дала  толчок  к  поиску  и  анализу  различных  формализаций  алгоритма.

Первые  фундаментальные  работы  по  теории  алгоритмов  были  опубликованы  независимо  в  1936  году  Аланом  Тьюрингом,  Алоизом  Черчем  и  Эмилем  Постом.  Предложенные  ими  машина  Тьюринга,  машина  Поста  и  лямбда-исчисление  Черча  были  эквивалентными  формализмами  алгоритма.  Важным  развитием  этих  работ  стала  формулировка  и  доказательство  алгоритмически  неразрешимых  проблем.

Существенный  вклад  в  теорию  алгоритмов  внесли  работы  Андрея  Андреевича  Маркова.  В  1940-х  годах  он  предложил  способ  формального  определения  понятия  алгоритма ,  названного  нормальным  алгоритмом  Маркова.  Марков  предположил,  что  любой  алгоритм  может  быть  записан  в  виде  нормального  «алгорифма».  Позднее  было  доказано,  что  нормальные  алгоритмы  Маркова  эквивалентны  по  своим  возможностям  другим  универсальным  исполнителям:  машине  Тьюринга   и  машине  Поста.

Для  реализации  цели  своей  работы,  я  решила  рассматривать  случаи  из  повседневной  жизни  как  программу  для  Машины  Тьюринга  и  как  нормальный  алгоритм  Маркова.

Нормальные  алгоритмы  Маркова  и  машина  Тьюринга

Нормальный  алгоритм  задает  метод  преобразования  строк  с  помощью  системы  подстановок.  Каждая  подстановка  состоит  из  слова-образца  и  слова-замены,  разделенных  цепочкой  символов  «→ ».  На  каждом  шаге  замены  подстановки  просматриваются  по  порядку  сверху  вниз,  и  выполняется  первая  из  них,  которая  подошла:  первое  найденное  слово-образец  рабочей  строки  заменяется  на  слово-замену.

Машина  Тьюринга  —  математическая  абстракция,  представляющая  вычислительную  машину   общего  вида.  Согласно  тезису  Тьюринга,  любой  алгоритм  может  быть  записан  в  виде  программы  для  машины  Тьюринга.

Машина  Тьюринга  состоит  из  каретки,  считывающей  и  записывающей  головки  и  бесконечной  ленты,  разбитой  на  ячейки.  Каждая  ячейка  ленты  может  содержать  символ  из  некоторого  алфавита  A={a₀,a₁,…,a_N}.  Любой  алфавит  содержит  символ  «пробел»,  который  обозначается  как  λ.

Машина  Тьюринга  —  это  автомат,  который  управляется  таблицей.  Строки  в  таблице  соответствуют  символам  выбранного  алфавита  A,  а  столбцы  —  состояниям  автомата  S={s₀,s₁,…,s_M}.  В  начале  работы  машина  Тьюринга  находится  в  состоянии  s₁.  Состояние  s₀  -  конечное  состояние.  Попав  в  него,  автомат  заканчивает  работу.

В  каждой  клетке  таблицы,  соответствующей  некоторому  символу  a_i  и  некоторому  состоянию  s_j,  находится  команда,  состоящая  из  трех  частей:

1.  символ  из  алфавита  A;

2.  направление  перемещения:  П  (вправо),  Л  (влево)  или  Н  (на  месте);

3.  новое  состояние  автомата.

Применение  теории  алгоритмов  к  ситуациям  из  повседневной  жизни

Пустые  места  или  «пробелы»  в  нормальных  алгоритмах  Маркова  ,  как  и  в  программах  для  машины  Тьюринга,  будем  обозначать  λ.

Ситуация  1:  прочитать  серию  книг

Представим  серию  книг  в  виде  последовательности  x₁  x₂  x₃..x_n  ,  где  n-номер  последней  книги  в  серии,  а  x_i  принимают  значения  а,  если  номер  книги  в  серии  нечетный,  и  b,если  четный.  По  окончании  работы  алгоритм  должен  напечатать  слово  bb.

Программа  для  машины  Тьюринга

Таблица  1. 

Программа  для  машины  Тьюринга  для  ситуации  1

Нормальный  алгоритм  Маркова

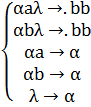
Проверим  работу  алгоритмов.  Возьмем  для  примера  серию  книг  «Властелин  колец»  Дж.Р.Р.  Толкина.  Серия  содержит  три  книги.  Значит,  слово,  на  котором  я  буду  проверять  работу  алгоритма  —  aba.

Программа  для  машины  Тьюринга:

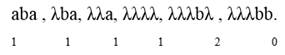
Нормальный  алгоритм  Маркова:

λabaλ  ,  αabaλ,  αbaλ,  αaλ,  bb.

Рассмотрим  еще  один  пример.  Серия  книг  «Гарри  Поттер»  Дж.К.  Роулинг.  Серия  содержит  семь  книг.

Программа  для  машины  Тьюринга:

Нормальный  алгоритм  Маркова:

λabababaλ,  αabababaλ,  αbababaλ,  αababaλ,  αbabaλ,  αabaλ,  αbaλ,  αaλ,  bb.

Ситуация  2:  доехать  до  некоторого  места  на  машине  и  обратно.

Представим  маршрут  в  виде  последовательности  x₁  x₂  x₃..x_n  ,  где  x_i  принимают  значения  R  —  поворот  направо,  L  —  поворот  налево,  D  —  движение  прямо.

По  окончании  работы  алгоритм  должен  «затереть»  входное  слово,  то  есть  напечатать  последовательность  пустых  символов.  Таким  образом,  нужно  пройти  входное  слово  слева  направо,  заменив  символы  R  на  L,  L  на  R,  и  оставив  символ  D,  а  затем  справа  налево,  заменив  все  символы  пустыми  символами.

Программа  для  машины  Тьюринга

Таблица  2. 

Программа  для  машины  Тьюринга  для  ситуации  2

Нормальный  алгоритм  Маркова

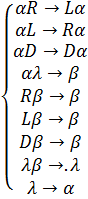
Проверим  работу  алгоритмов.  Возьмем  маршрут  RRLDLDRRRDL

Программа  для  машины  Тьюринга:

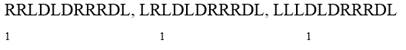
Продолжая  работу  алгоритма  получим  :

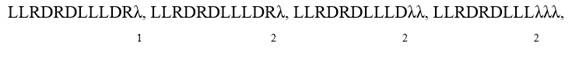
Продолжая  работу  алгоритма  получим  :

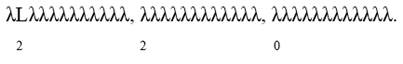
Нормальный  алгоритм  Маркова:

λRRLDLDRRRDLλ,  αRRLDLDRRRDLλ,  LαRLDLDRRRDLλ,  LLαLDLDRRRDLλ

Продолжая  работу  алгоритма  получим  :

LLRDRDLLLDRαλ,  LLRDRDLLLDRβ,  LLRDRDLLLDβλ,  LLRDRDLLLβλλ

Продолжая  работу  алгоритма  получим  :

λlβλλλλλλλλλλ,  λβλλλλλλλλλλ,  λλλλλλλλλλλ.

Ситуация  3:  выполнить  комплекс  физических  упражнений.

Представим  комплекс  физических  упражнений  в  виде  последовательности  x₁  x₂  x₃x₄λ  x₅  x₆  x₇x₈  λ  x₉  x₁₀  x₁₁x₁₂,  где  x_i  принимают  значения  четырех  базовых  упражнений  a,b,c,z.  После  каждых  четырех  упражнений  —  отдых,  обозначенный  пустым  символом  λ.  Комплекс  выполняется  дважды. 

По  окончании  работы  алгоритм  должен  «затереть»  входное  слово,  то  есть  напечатать  последовательность  пустых  символов.  Таким  образом,  нужно  дважды  пройти  входное  слово  слева  направо,  не  изменяя  его  при  первом  проходе,  и  заменяя  все  символы  на  «пробел»  при  втором  проходе.

Программа  для  машины  Тьюринга

Таблица  3. 

Программа  для  машины  Тьюринга  для  ситуации  3

Нормальный  алгоритм  Маркова

Проверим  работу  алгоритмов.  Возьмем  комплекс  упражнений  aabbλbzbcλcczb.

Программа  для  машины  Тьюринга:

Нормальный  алгоритм  Маркова:  λaabbλbzbcλcczbλλ,  αaabbλbzbcλcczbλλ,  aαabbλbzbcλcczbλλ,  aaαbbλbzbcλcczbλλ.

Продолжая  работу  алгоритма  получим:  aabbλbzbcλcczbαλλ,  aabbλbzbcλcczbβ,  aabbλbzbcλcczβb,  aabbλbzbcλccβzb.

Продолжая  работу  алгоритма  получим:  λλβaabbλbzbcλcczb,  γaabbλbzbcλcczb,  λγabbλbzbcλcczb,  λλγbbλbzbcλcczb.

Продолжая  работу  алгоритма  получим:  λλλλλλλλλλλλλλλγbλλ,  λλλλλλλλλλλλλλλγλλ,  λλλλλλλλλλλλλλλ.

Заключение

Выполняя  исследовательскую  работу,  я  убедилась,  что  математика,  это  не  только  сухие  законы,  теоремы  и  формулы.  Математика  во  многом  творческий  процесс.  Составление  алгоритмов  для  рассмотренных  примеров  потребовало  от  меня  посмотреть  на  обыденные  вещи  под  другим  углом.  И  представленные  мною  решения  вовсе  не  единственные.

Подобные  нестандартные  задания  позволяют  с  фантазией  подходить  к  их  решениям,  что,  безусловно,  способствуют  развитию  интереса  к  математике  и  теории  алгоритмов  в  частности.

Список  литературы:

1.Машина  Тьюринга.Тренажер  для  изучения  универсального  исполнителя  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://kpolyakov.narod.ru/prog/turing.htm   (дата  обращения  7.04.2015).

2.Носов  В.А  Основы  теории  алгоритмов  и  сложности  их  анализа  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.ict.edu.ru/ft/003139/theoralg.pdf   (дата  обращения  8.04.2015). 3.Подзоров  С.Ю  Теория  алгоритмов.  Полный  конспект  лекций  по  курсу  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.nsu.ru/education/podzorov/Alg/Course.pdf   (дата  обращения  8.04.2015). 4.Теория  алгоритмов.  Введение  в  теорию  алгоритмов  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://th-algoritmov.narod.ru/1.htm   (дата  обращения  7.04.2015).

5.Тишин  В.В.  Дискретная  математика  в  примерах  и  задачах  СПб.:  БХВ-Петербург,  2008  —  352  с.