АНАЛИЗ  ГЕНЕРАТОРА  ПСЕВДОСЛУЧАЙНЫХ  ЧИСЕЛ  С  ПОМОЩЬЮ  СТАТИСТИЧЕСКИХ  ТЕСТОВ

Димитренко  Егор  Владимирович

E -mail:  Egoka93@yandex.ru

Швецов  Александр  Юрьевич

студенты  3  курса  факультета  информатики  СГАУ  им.  Академика  Королева,  РФ,  г.  Самара

E -mail:  shvetsovalex007@gmail.com

Тишин  Владимир  Викторович

научный  руководитель,  доцент,  кафедра  прикладной  математики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

Генерация  случайных  чисел  —  процесс,  направленный  на  получение  последовательности  независящих  друга  от  друга  чисел,  подчиняющихся  некому  закону  распределения.  Область  применения  случайных  чисел,  занимает  многие  ниши  в  информационных  технологиях.

Выделяют  два  вида  генераторов

·     Аппаратный  генератор  случайных  чисел  (АГСЧ)

·     Генератор  псевдослучайных  чисел  (ГПСЧ)

Аппаратный  генератор  случайных  чисел  —  некое  устройство,  генерирующее  последовательность  случайных  чисел,  используя  характеристики  протекающего  физического  процесса.  Работа  устройства  основывается  на  использовании  накопленных  источников  энтропии:

·     Радиоактивный  распад

·     Фотоэффект

·     Дробовой  шум

По  сути,  весь  окружающий  наш  мир,  это  огромный  генератор  случайных  величин.  Хоть  величины  получаются  псевдослучайны,  но  всем  этим  закономерностям  нельзя  прописать  общий  закон,  из-за  бесконечного  множества  вариантов  развития  происходящих  событий. 

Проблемы,  возникающие  в  данном  подходе  генерации  случайной  величины:

·     Низкая  скорость  по  сравнению  с  ГПСЧ

·     Короткий  срок  эксплуатации 

Генератор  псевдослучайных  чисел  —  генерация  случайной  величины  происходит  заданным  алгоритмом.  В  отличие  от  АГСЧ,  где  использовалась  накопленная  энтропия,  в  данном  подходе  используется  единственное  начальное  значение.  Именно  из-за  этого  подхода,  случайная  величина  в  данном  случае  называется  псевдослучайной.

На  практике  АГСЧ  используется  чаще  всего  в  исследовательских  целях,  поэтому  в  дальнейшем  мы  будем  рассматривать  ГПСЧ,  из-за  его  широкого  приложения  в  информационных  технологиях  и  криптографии,  а  именно:

·     Генерация  ключей  для  ассиметричных  шифров

·     Генерация  паролей

·     В  компьютерном  моделировании

·     В  игровых  целях

Одна  из  проблем  ГПСЧ,  это  появляющиеся  проблемы  уязвимости:

·     Прогнозируемая  зависимость  между  случайными  величинами

·     Прогнозируемое  начальное  значение  алгоритма

·     Слишком  короткий  период  повторения

Например,  для  моделирования  поведения  какой-либо  случайной  величины  отлично  подойдет  такой  генератор,  обладающий  высокой  скоростью  генерации  новых  элементов,  но  для  моделирования  не  обязательна  криптографическая  стойкость.  Для  использования  в  криптографических  системах,  использующих  симметричное  или  ассиметричное  шифрование  напротив,  криптостойкость  ГПСЧ  выходит  на  первое  место.  В  нашей  работе  мы  хотели  бы  рассмотреть  генерацию  псевдослучайных  последовательностей  именно  для  криптографических  систем. 

Рассмотрим  алгоритм  Блюм-Блюма-Шуба  и  проверим  [1].  Генерация  нового  значения  происходит  следующим  образом:

x_{n  +  1}  =  x_n²(mod  M),

где:  x_n  —  новый  элемент  последовательности, 

x_n-1  —  предыдущий  элемент, 

M  =  p*q,  где  p  и  q  большие  простые  числа.  Выходными  данными  на  каждом  шаге  алгоритма  являются  бит  четности  x_n  или  несколько  битов  наименьшей  значимости  x_n.  На  числа  p  и  q  накладываются  так  же  дополнительные  ограничения,  p  =  q  =  3  (mod  4).  Это  обеспечивает  достаточную  длину  цикла  без  повторений,  что  необходимо  для  генерации  достаточного  количества  псевдослучайных  чисел.  Еще  одно  условие,  что  начальное  значение    должно  быть  взаимно  простым  с  M.  Особенностью  данного  алгоритма  является  то,  что,  зная  начальное  состояние  генератора,  а  также  числа  p  и  q,  можно  восстановить  любой  член  последовательности,  не  считая  предыдущие  (рис.  1).

Благодаря  сложности  задачи  факторизации  числа  М,  невозможно  за  полиномиальное  время  подобрать  нужные  числа  p  и  q,  чтобы  остановить  нужные  биты  последовательности.  То  есть,  если  p  и  q  удовлетворяют  всем  вышеизложенным  условиям,  не  существует  такого  полиномиально-временного  алгоритма,  с  помощью  которого  можно  было  бы  предсказать  появление  следующего  бита  с  вероятностью  более  пятидесяти  процентов,  что  обеспечивает  криптостойкость  алгоритма

Итак,  мы  имеем  алгоритм  ГПСЧ,  но  можно  ли  сказать,  что  любая  последовательность,  получаемая  с  помощью  него,  действительно  является  случайной?  Из  определения  случайно  величины:  Это  величина,  принимающая  в  результате  опыта  одно  из  множества  значений,  и  появление  ни  одного  значения  нельзя  точно  предсказать  до  ее  измерения.  Таким  образом,  имея  заранее  сгенерированную  последовательность  чисел,  стоит  задача  определить,  не  являются  ли  значения  в  ней  связны  или  принадлежащими  к  какому-нибудь  закону  распределения.  Для  решения  этой  задачи  используют  статистические  тесты. 

Статистические  тесты  —  один  из  видов  тестирования  ГПСЧ,  который  выдает  численную  характеристику  последовательности  и  позволяет  однозначно  выявить,  пройден  ли  тест.  Многие  исследовательские  институты  и  центры  составляют  и  усовершенствуют  различные  статистические  тесты.  Наиболее  известные:

·     DIEHARD

·     NIST 

·     CRYPT-X

Для  проверки  последовательности,  полученной  с  помощью  алгоритма  Блюм-Блюм-Шуба,  мы  выбрали  тесты  NIST,  из-за  открытого  исходного  кода  всех  тестов. 

Статистические  тесты  NIST  —  пакет  статистических  тестов,  разработанный  Национальным  институтом  стандартов  и  технологий.  В  состав  пакета  входит  15  тестов,  определяющих  меры  случайности  двоичных  последовательностей  полученными  с  помощью  ГПСЧ  или  АГСЧ.  Эти  тесты  основаны  на  различных  статистических  свойствах,  присущих  только  случайным  последовательностям.  Рассмотрим  некоторые  из  них[3]:

·     Частотный  побитовый  тест  —  проверка  соотношения  между  нулями  и  единицами  в  последовательности  и  насколько  близко  доля  нулей  к  0.5.  Если  значение  вероятности  p<0.01,  то  последовательность  не  является  истинно  случайно.  Отметим,  что  дальнейшие  тесты  проходятся  только  в  случае  прохождения  данного

·     Тест  на  одинаковые  идущие  подряд  биты  —  проверка  всех  под  последовательностей  одинаковых  битов  на  их  размер  и  количество,  относительно  истинно  случайной  последовательности.  Если  ноль  и  единица  чередуются  слишком  редко,  то  последовательность  сложно  назвать  случайной.

Для  прохождения  теста  было  сгенерировано  две  последовательности  длинной  10000  бит.  При  получении  первой  последовательности  были  выполнены  все  ограничения,  накладываемые  на  начальные  параметры  генератора:

·     p  и  q  были  выбраны  такие,  чтобы 

·     M  и    взаимно  простые

Для  второй  последовательности  было  не  соблюдено  первое  и  второе  ограничение.  Таким  образом,  при  проверке  наших  последовательностей  на  тестах  NIST,  с  помощью  свободно  распространяемого  пакета  под  операционную  систему  Linux  были  получены  результаты  для  первой  (рис.  1)  и  для  второй  (рис.  2)  последовательности.  Из  большинства  тестов  видно,  что  первая  последовательность  в  большей  степени  удовлетворяет  критериям  случайности.

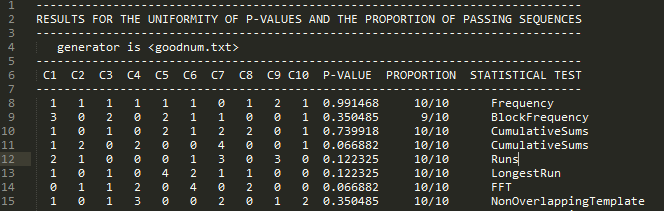
Рисунок  1.  Результаты  тестов  для  первой  последовательности

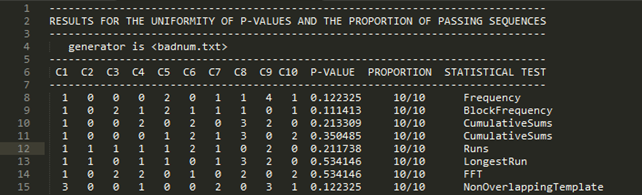
Рисунок  2.  Результаты  тестов  для  второй  последовательности

Подводя  итог  проделанной  работе,  можно  сказать  следующее:

·     Мы  нашли  оптимальный  алгоритм  для  генерации  псевдослучайных  последовательностей,  используемых  в  криптосистемах

·     Познакомились  с  особенностями  и  условиями  работы  алгоритма  Блюм-Блюм-Шуба

·     Выявили,  что,  при  правильном  построении  алгоритма,  данный  генератор  проходит  статистические  тесты,  что  говорит  о  его  пригодности  для  выбранных  целей

Список  литературы:

1.Гнеденко  Б.В.  «Курс  теории  вероятностей»,  М.:  Наука,  1988.

2.Дональд  Кнут.  Искусство  программирования,  том  2.  Получисленные  методы  =  The  Art  of  Computer  Programming,  vol.2.  Seminumerical  Algorithms.  3-е  изд.  М.:«Вильямс»,  2007.  —  832  с.  —  ISBN  5-8459-0081-6.

3.Andrew  Rukhin,  Juan  Soto,  James  Nechvatal  A  Statistical  Test  Suite  for  Random  and  Pseudorandom  Number  Generators  for  Cryptographic  Applications  April  2010  //Computer  Security  Division  Information  Technology  Laboratory  National  Institute  of  Standards  and  Technology  Gaithersburg,  MD  20899-8930  Режим  доступа:  http://csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22rev1a.pdf,  свободный.  Загл.  с  экрана.  Яз.  рус.,  англ.  (дата  обращения  25.04.2015).