ТЕОРИЯ  РЯДОВ  КАК  ОСНОВА  СОЗДАНИЯ  МУЗЫКАЛЬНОГО  ПРОИЗВЕДЕНИЯ

Скирко  Данила  Владимирович

студент  2  курса,  кафедра  судовождения  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет»,  РФ,  г.  Керчь

E -mail:  skirko.danila@yandex.ru

Скирко  Никита  Владимирович

студент  2  курса,  кафедра  судовождения  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет»,  РФ,  г.  Керчь

E -mail:  nikita.bear@mail.ru

Егорова  Светлана  Николаевна

научный  руководитель,  кафедра  высшей  математики  и  физики  ФГБОУ  ВО  «Керченский  государственный  морской  технологический  университет,  РФ,  г.  Керчь

Каждое  новое  открытие  заставляет  ставить  перед  собой  целый  ряд  новых  вопросов:  а  возможно  ли,  почему,  как  и  зачем.  С  развитием  математики  и  появлением  мощного  программного  обеспечения,  которое  позволило  описать  все  законы  гармонии,  возник  интерес  к  написанию  музыки  с  помощью  рядов.

Большую  популярность  эта  идея  приобрела  с  появлением  Новой  венской  школы.  Арнольд  Шенберг  и  Антон  Веберн  возглавили  неизведанное  до  этого  течение,  создав  свои  произведения  на  основе  математики,  придав  новые  краски  музыке  (самому  консервативному  в  то  время  творческому  направлению). 

Следующим  шагом  в  этом  направлении  стали  программы,  с  помощью  которых  каждый  человек  может  создать  свою  неповторимую  композицию.  Это  стало  возможным  благодаря  совершенно  новым  открытиям  в  области  математики,  к  примеру,  фракталам.  Это  молодое  направление  математики  открыло  десятки  путей  для  создания  музыки.

В  нашей  работе  мы  решили  провести  параллель  между  созданием  музыкальных  композиций  посредством  законов  гармонии  и  математики,  исследовать  связь  между  теорией  рядов  и  структурой  музыкального  произведения,  попытаться  на  основе  созданной  мелодии  определить  закон,  по  которому  она  изменяется.

Интерес  к  созданию  музыки  с  помощью  математического  расчета  был  замечен  еще  в  Средневековье,  когда  музыка  как  предмет  изучалась  наравне  с  другими  науками.  Уже  тогда  музыку  включали  в  раздел  математики,  хотя  само  понятие  «математика»  сильно  отличалось  от  нынешнего.

Первыми,  кто  заинтересовался  этим  вопросом,  стал  Пифагор,  который  заметил,  что  отношение  частот  двух  соседних  нот  всегда  отличается,  но  в  тоже  время,  ноты,  отстоящие  друг  от  друга  на  четыре  позиции,  имеют  одинаковую  частоту,  равную  3/2  (сегодня  такой  интервал  называется  квинтой).  Узнав  это,  Пифагор  смог  вывести  математическую  формулу,  которая  позволила  ему  найти  частоту  последующей  ноты.  Таким  образом,  он  получил  все  звуки  звукоряда,  но  создал  новую  дилемму:  звукоряд  не  укладывался  в  целое  число  октав,  что  позже  назвали  «пифагорова  комма»  [6]. 

Выход  их  данного  парадокса  нашел  Веркмейстер,  введя  три  основных  правила:

·       отношение  частот  одинаковых  нот  в  соседних  октавах  должно  быть  равно  двум;

·       между  этими  частотами  должно  лежать  ровно  двенадцать  нот,  по  числу  полутонов  в  октаве;

·       все  полутона  должны  быть  равны.

Это  позволило  ему  разбить  октаву  на  двенадцать  равных  полутонов.  Сегодня  такой  звукоряд  называется  темперированным  (одноименные  интервалы  стали  одинаковыми  по  величине).  Но  математический  мир  не  стоял  на  месте  и  с  каждым  столетием  приобретал  привычные  для  нас  формы,  углубляясь  в  самые  недра,  чего  не  скажешь  о  музыке. 

До  начала  XX  века  музыка  имела  предпочтительно  мажорно-минорную  тональность,  что  привело  к  своего  рода  «кризису».  Именно  он  подтолкнул  композиторов  к  мысли,  что  придерживаться  одной  тональности  необязательно  или  вовсе  не  нужно.  Это  стало  зародышем  новой  волны  поисков,  в  числе  которых  особенно  выделяется  понятие  «серийности».

По  определению,  серийная  музыка  —  это  техника  музыкальной  композиции,  использующая  в  качестве  звуковысотной  основы  музыкального  произведения  ряд  неповторяющихся  звуков  [4,  с.  275].

Но  само  определение  является  слишком  расплывчатым,  так  как  не  несет  в  себе  какого-либо  точного  закона  либо  правила,  по  которому  могла  бы  строиться  мелодия.  Именно  поэтому  представители  Новой  венской  школы  (нововенцы)  во  главе  с  Арнольдом  Шенбергом  и  Антоном  Веберном  реформировали  данную  технику,  заменив  тональные  основы  музыки  на  специальные  атональные  техники. 

Додекафония  стала  наиболее  яркой  теорией,  основной  принцип  которой  —  недопустимость  повторения  во  времени  одноименных  звуков  до  тех  пор,  пока  не  будут  исчерпаны  все  12  звуков,  на  которые  делится  октава  в  рамках  темперированного  строя.  Последовательность  12  неповторяющихся  звуков  и  образует  серию.  Серия  является  основным  элементом  всей  музыкальной  композиции. 

Ее  можно  представить  в  виде  упорядоченного  набора  чисел  в  пределах  от  0  до  11,  пронумеровав  звуки  по  порядку:  0  =  до,  1  =  до-диез,  2  =  ре,  …  10  =  си-бемоль,  11  =  си,  12  =  0  (по  модулю  12)  =  до  (два  звука  считаются  равными,  если  соответствующие  им  числа  равны  по  модулю  12)  [2]. 

Для  осуществления  математических  операций  над  различными  формами  серий  можно  представить  серию  в  виде  пар.  Пара  представляет  собой  «координаты  звука»  —  упорядоченный  набор  из  двух  чисел,  первое  число  —  это  номер  звука  в  серии,  второе  число  —  высота  тона  [5].

Веберн,  в  свою  очередь,  подбирал  серии,  которые  имели  внутреннюю  симметрию,  строя  при  этом  целые  музыкальные  схемы  (рис.  1). 

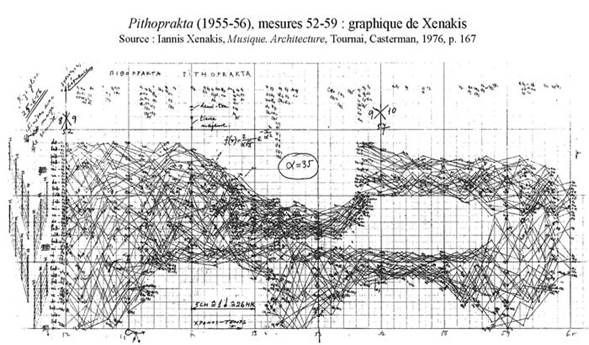
Рисунок  1.  Схема  музыкальной  партитуры

Проблемы,  возникшие  перед  теорией  музыки,  были  самые  разноплановые.  Прежде  всего,  требовалось  осмыслить  появившуюся  12-тоновость  в  аспекте  ее  разнообразной  типологии  и  новой  функциональной  структуры.  Затем  возникла  необходимость  создания  универсальной  теории  звуковысотности,  которая,  охватывая  все  эпохи,  вывела  бы  общие  закономерности  функционирования  гармонии  независимо  от  конкретных  звуковысотных  систем.  И,  наконец,  одной  из  важнейших  задач  стала  выработка  нового  аналитического  метода,  адекватного  специфике  12-тоновой  композиции. 

Подобные  исследования,  связанные  с  теорией  рядов,  стали  использоваться  для  глубокого  анализа  произведений  музыки  исполнителей  60-х  годов,  но  слабо  применимы  для  ее  создания  [1].

В  нашем  исследовании  мы  попытались  создать  собственную  композицию,  применив  теорию  рядов. 

Сегодня,  в  эпоху  новых  технологий,  которые  давно  превосходят  возможности  человека  (по  разным  факторам),  активно  развивается  создание  программ,  которые  могли  бы  помочь  человеку  создать  свою  композицию,  даже  не  имея  музыкального  образования.  Данные  программы  создаются  на  основе  законов  гармонии  и  математики,  которые  и  дают  возможность  создавать  приятные  для  слуха  произведения.

Математика  играет  важную  роль,  ведь  с  помощью  нее  мы  задаем  начальное  условие  мелодии.  Тональность,  мотив,  размер  и  сама  структура  —  все  это  позволяет  нам  в  дальнейшем  не  ошибиться  и  создать  желаемое.  Любая  мелодия  состоит  из  нескольких  основных  мотивов,  которые  задают  и  настраивают  слушателя  на  тональность.

Создадим  простейший  мотив  и  присвоим  ему  название  «а».  Для  его  создания  воспользуемся  специальной  программой  Palette  [7].  Ее  автор  сумел  перевести  основные  законы  гармонии,  правила  голосоведения  и  приемы  развития  мелодии  на  язык  математических  алгоритмов,  создав,  своего  рода,  калькулятор  музыкальных  произведений. 

Отличительная  особенность  Palette  заключается  в  том,  что  программа  лишь  предлагает  варианты  развития  короткого  исходного  фрагмента  мелодии,  придуманного  человеком.  Да  и  в  дальнейшей  работе  над  композицией  роль  человека  не  сводится  только  к  фиксированию  наиболее  удачного  «экземпляра»  музыки,  созданного  компьютером.  В  нашей  власти  выбор  алгоритмов  и  сочетаний  их  параметров.  И  тех,  и  других  в  Palette  очень  много  и  они  заметно  влияют  на  конечный  результат.  Эта  программа  не  превращает  музыканта  в  пассивного  наблюдателя  за  сменой  картинок  на  экране,  а  сохраняет  за  ним  все  основные  функции  творца.

По  сути  дела  Palette  —  что-то  вроде  специализированного  музыкального  калькулятора,  на  который  возложена  задача  избавления  сочинителя  музыки  от  рутинной  работы.  А  в  остальном  все  зависит  от  человека:  что  введешь  в  калькулятор,  то  и  получишь.

В  основу  программы  Palette  положена  модель,  базирующаяся  на  традиционных  теориях  гармонии  и  математики,  в  том  числе  и  теории  рядов  [3].

Рисунок  2.  Мотив  «а»

Созданный  нами  мотив  (рис.  2)  стал  началом  нашей  композиции.  Для  его  создания  нам  понадобилось  присвоить  ему  собственное  имя,  куда  мы  вложили  размерность  каждой  ноты,  которая  точно  соответствует  нашему  размеру  такта  2/4  и  позицию  каждой  ноты.  Следующий  такт  и  все  последующие  будут  развитием  мотива  «а».

Добавив  следующий,  мы  получим  целую  фразу,  которой  так  же  присвоим  свое  название  —  «А». 

В  данной  небольшой  композиции  можно  на  примере  показать  серийную  технику,  которая  будет  заключаться  в  использовании  серий,  в  нашем  случае  —  мотивов.

Рисунок  3.  Развитие  мотива  «а»

Третий  фрагмент  нашей  композиции  мы  написали  на  основе  первого,  но  чтобы  создать  законченное  предложением,  мы  заканчиваем  второе  предложение  разрешением  аккорда,  который  использовали  в  последнем  такте. 

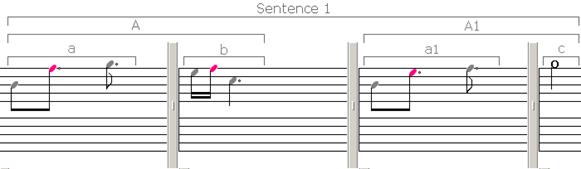
Рисунок  4.  Первое  предложение  композиции

В  итоге  мы  получаем  законченное  предложение  (рис.  4).  Если  записать  данное  предложение  в  ряд,  то  мы  получим  следующую  последовательность,  присвоив  каждому  мотиву  свое  значение:

a +b+a1+c+…

Исходя  даже  из  этого  небольшого  ряда,  программа  сможет  создать  целое  произведение,  которое  будет  перемешивать  это  предложение  до  тех  пор,  пока  не  закончатся  возможные  варианты  тональностей. 

Минусом  серийной  техники,  в  данном  случае,  будет  являться  ограниченность,  так  как  серийность  использует  не  более  12  звуков.

Продолжив  композицию  по  тому  же  принципу,  выводим  второе  предложение,  где  будут  отличаться  некоторые  такты  (рис.  5):

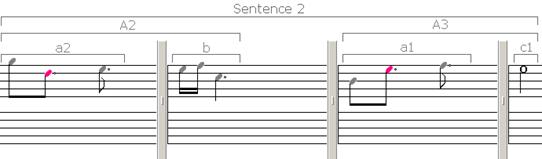
Рисунок  5.  Второе  предложение  композиции

Стоит  сразу  заметить,  что  фрагменты  «а2»  и  «с1»  будут  иметь  противоположные  знаки,  потому  что  они  будут  обращением  «а1»  и  «с». 

Соединяем  два  предложения  и  получаем  целую  мелодию  (рис.  6):

Рисунок  6.  Соединенная  композиция  из  первого  и  второго  предложения

a +b+a1+c+a2+b+a1+c1+…

Если  записать  его  в  более  правильном  виде,  то  он  сводится  к  простейшему  ряду:  1+2+3+…,  т.к.  мелодия  является  односложной  и  линия,  по  которой  идет  мелодия,  не  разветвляется,  тем  самым  не  позволяя  разнообразить  общую  композицию.

Закон,  по  которому  изменяется  наша  мелодия,  прост:  ∑n+1,  потому  что  с  каждым  новым  тактом  мелодия  принимает  одно  новое  общее  значение,  увеличивая  общее  количество  мотивов  на  1.

В  теории,  запись  любого  произведения  возможна  даже  без  участия  музыкальных  инструментов  и  программ,  главное,  что  необходимо  —  это  грамотное  присвоение  каждому  мотиву  значения  и  знание  гармонии.

В  результате  наших  исследований  мы  сделали  вывод  о  том,  что  использование  теории  рядов  для  создания  собственных  композиций  является  лишь  основой,  ведь  она  пригодна  для  создания  единичной  мелодии  или  партии.  Для  создания  более  сложных  композиций,  которые  будут  включать  в  себя  несколько  равноправных  мелодий,  требуются  новые  ресурсы.

Сегодня  более  совершенным  средством  являются  поющие  фракталы,  которые  являются  новым  направлением  не  только  в  создании  музыки,  но  и  в  математике  в  частности.  Они  позволяют  учесть  все  аспекты  композиции  и  записать  их  в  единичном  коде,  вложив  всю  необходимую  информацию  с  помощью  специальных  программ.  Далее,  посредством  законов  гармонии,  нужно  будет  свести  несколько  отдельных  мелодий  воедино  таким  образом,  чтобы  их  звучание  было  приятным  и  темперированным.

Наши  исследования  на  этом  не  заканчиваются,  и  следующая  работа  будет  посвящена  созданию  собственной  композиции  с  помощью  поющих  фракталов,  которые  открывают  ряд  возможностей  для  совершенствования  мелодии. 

Список  литературы:

1.Изотова  Е.А.  Теория  рядов  в  свете  американской  музыкальной  науки  60-80-х  гг.  XX  века:  дис….канд.  искусствоведения  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  http://www.dissercat.com/content/teoriya-ryadov-v-svete-amerikanskoi-muzykalnoi-nauki-60-80-kh-gg-xx-veka   (дата  обращения:  15.12.2014).

2.Петелин  Ю.В.  Математика  плюс  музыка  //  Музыка  —  Компьютер  [Электронный  ресурс].  —  Режим  доступа.  —  URL:  —http://www.petelin.ru/pcmagic/math/math.htm/  (дата  обращения:  15.12.2014).

3.Петелин  Ю.В.  Palette  -  гармония,  поверенная  алгеброй  //  Музыка  –  Компьютер  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.petelin.ru/pcmagic/palette/palette.htm  (дата  обращения:  15.12.2014).

4.Холопов  Ю.Н.  Додекафония  //  Музыкальная  энциклопедия  в  6  томах.  М.:  БСЭ,  1973—1982.  —  Т.  2.

5.Черненко  В.  Как  писать  музыку  с  помощью  математики  //  Zellion  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://zillion.net/ru/blog/241/kak-pisat-muzyku-s-pomoshch-iu-matiematiki   (дата  обращения:  15.12.2014).

6.Шипилов  А.  Хорошо  темперированный  PC  //  Компьютера:  научн.  нтернет-журнал.  17.11.1997.  —  №  46  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://old.computerra.ru/offline/1997/223/893/   (дата  обращения:  14.12.2014).

7.The  Palette  —  Melody  Composing  Tool  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.palette-mct.com/  (дата  обращения:  15.12.2014).