Статья опубликована в рамках: XXIX Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 февраля 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ МИРА ФРАКТАЛОВ
Васильева Марина Владимировна
студент 3 курса, факультет информатики СГАУ им. академика С.П. Королева, РФ, г. Самара
E -mail: vasmarishka1994@mail.ru
Тишин Владимир Викторович
научный руководитель, доцент, кафедра прикладной математики СГАУ
им. академика С.П. Королева, РФ, г. Самара
Введение
Мир фракталов — это удивительный, огромный и многообразный мир. Он очаровывает, покоряет, однако иногда в нем трудно разобраться. Фрактальные рисунки — это пик вдохновения мастера на пути к совершенному единству математики, информатики и искусства. Недавно геометрические модели природных объектов изображались с помощью комбинаций простых фигур, таких как прямые, треугольники, окружности, сферы, многогранники. Но с помощью набора этих известных фигур нелегко описать более сложные природные объекты, например, пористые материалы, формы облаков, кроны деревьев. Новые компьютерные средства, без которых не может обойтись современная наука, выводят математику на чрезвычайно высокий уровень. Когда изучаешь фракталы, понимаешь, что весьма затруднительно провести грань между математикой и информатикой, потому что они тесно переплелись, стремясь открыть неповторимые, уникальные модели. Фракталы приближают нас к пониманию некоторых природных процессов и явлений. Поэтому тема фракталов меня заинтересовала.
Передо мной возникла проблема: как построить фрактал, используя математические формулы.
Гипотеза: если изучить закономерности построения фракталов, то их можно смоделировать.
Методы исследования: анализ, синтез, моделирование.
Цель: построить фракталы с помощью компьютерных технологий.
Задачи: исследовать фракталы; изучить историю возникновения и применения фракталов.
Актуальность: я считаю — за фракталами будущее, они лучше передают наш изменчивый и сложный мир. Фракталы помогают изучить различные процессы и явления.
Результат исследования: разработка алгоритма построения фракталов.
Теоретическая и практическая значимость: использование алгоритма построения фракталов для изучения их свойств.
Понятие «фрактал»
Понятия «фрактал» и «фрактальная геометрия» появились в 70—80-х годах XX века. Они устойчиво закрепились в употреблении математиков и программистов. Слово «фрактал», что в переводе с латинского означает разбитый, поделённый на части, было предложено Бенуа Мандельбротом, американским математиком, в 1975 году, с целью обозначения нерегулярных самоподобных структур. Мандельброт дал такое определение: «фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». Следует отметить, что свойство самоподобности отражает главную особенность природных объектов.
С точки зрения математики, фрактал — это, в первую очередь, множество дробной размерности. Известно, что размерность отрезка равна 1, квадрата — 2, куба и параллелепипеда — 3. Дробная размерность — это основное свойство фракталов.
С выходом книги Мандельброта «Фрактальная геометрия природы» в 1977 году связывают рождение фрактальной геометрии. В ней применены научные результаты учёных, среди них Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф, работавших в период 1875—1925 гг. в той же области. И только в наше время удалось объединить в единую систему эти работы.
Фрактальная геометрия является революцией в математике и математическом описании природы. Сам Бенуа Мандельброт, первооткрыватель фрактальной геометрии, пишет об этом так: «Облака — это не сферы, горы — это не конусы, линии берега — это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах бесконечно».
Рассматривая фрактальные объекты в различном масштабе, можно легко обнаружить одни и те же основные элементы. Закономерности, которые повторяются, определяют дробную размерность необычной геометрической фигуры.
Классификация фракталов
Удобно прибегнуть к их общепринятой классификации, чтобы представить все многообразие фракталов. Фракталы делятся на геометрические, алгебраические и стохастические.
К геометрическим фракталам относятся: кривая Коха, кривая дракона, кривая Леви, кривая Минковского, треугольник Серпинского, ковер Серпинского, множество Кантора и дерево Пифагора.
Такого класса фракталы самые наглядные, так как в них сразу видна самоподобность. В двухмерном случае их можно получить с помощью ломаной, которая называется генератором, в трехмерном случае — поверхности. Каждый из отрезков, составляющих ломаную, за один шаг алгоритма, заменяется на ломаную-генератор, в соответствующем масштабе. Таким образом, получается фрактальная кривая в результате бесконечного повторения этой процедуры. При видимой сложности полученной кривой, её общий вид задается только формой генератора.
Алгебраические фракталы: множество Мандельброта, множество Жюлиа, бассейны Ньютона, биоморфы.
Алгебраические фракталы являются самыми многочисленными. Для построения алгебраических фракталов используются итерации нелинейных отображений, которые задаются простыми алгебраическими формулами. Двухмерные процессы считаются наиболее изученными. Следует отметить, что нелинейные динамические системы имеют несколько устойчивых состояний. От начального состояния зависит то состояние, в котором оказалась динамическая система после некоторого числа итераций. Возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры стала для математиков неожиданностью.
К стохастическим фракталам относятся плазма и рандомизированный фрактал.
Термин «стохастичность» происходит от греческого слова и обозначает «предположение».
Как бы ни была похожа на границу берега, кривая Коха не может быть в качестве её модели, потому что она всюду одинакова, самоподобна и, можно сказать, слишком «правильна». Все природные объекты создаются по капризу природы, в этом процессе всегда есть случайность. Стохастическими фракталами называются такие фракталы, при построении которых случайным образом в итеративной системе изменяются какие-либо параметры. При этом получаются очень похожие на природные объекты такие, как несимметричные деревья, изрезанные береговые линии. При моделировании рельефа местности и поверхности моря используются двумерные стохастические фракталы.
Применение фракталов
Главным применением фракталов является современная компьютерная графика. С их помощью можно создавать плоские множества и поверхности очень сложной формы, изменяя при этом параметры в заданных уравнениях.
Фрактальная геометрия является незаменимой при генерации искусственных облаков, горных ландшафтов, морей. Учёные нашли простой способ изображения сложных объектов, у которых образы напоминают природные формы.
Наиболее полезным использованием фракталов в компьютерной науке считается фрактальное сжатие данных. Основой такого вида сжатия служит то, что фрактальной геометрией достаточно хорошо описывается реальный мир. Картинки при этом сжимаются даже намного лучше, чем с помощью обычных методов. При увеличении картинки не наблюдается эффекта пикселизации, в этом заключается еще одно преимущество фрактального сжатия. При фрактальном сжатии после увеличения картинка часто выглядит даже лучше, чем до него.
Следует отметить, что фракталы применяются в шифрование данных с помощью фрактальных алгоритмов.
Для передачи данных на расстояние используются антенны, которые имеют фрактальные формы, что сильно уменьшает их вес и размеры.
Также с помощью фракталов можно моделировать сложные физические процессы, например, языки пламени. Фрактальные формы достаточно хорошо передают пористые материалы, имеющие очень сложную геометрическую структуру. Такие знания используются в науке о нефти.
Теория фракталов применяется и при изучении структуры Вселенной.
В биологии можно рассмотреть такие примеры, как биосенсорные взаимодействия и биения сердца, моделирование хаотических процессов. Фракталы используют в своих произведениях и художники, и дизайнера, и композиторы.
Алгоритмы построения фракталов
Рассмотрим множество Мандельброта. В математике множество Мандельброта — это фрактал, который определяется как множество точек на комплексной плоскости, итеративная последовательность не уходит в бесконечность и задана формулами z0=0, Zn+1=Zn2+M. Чтобы построить данную последовательность точек, т. е. фрактал, перейдем от комплексной формы записи с помощью преобразований к удобным формулам для построения.
Если выражение Zn+1=Zn2+M переформулировать в виде итеративной последовательности значений координат комплексной плоскости x и y, то есть, приняв Z = X + iY и М = p + iq (где i — мнимая единица), то получим алгоритм с формулами (1): Xn+1=Xn2–Yn2+p; Yn+1=2XnYn+q, с параметрами p = – 0,5219;
q = 0,4999.
Сначала полагаем Xn = 0; Yn = 0, и по формулам (1) получаем на первом шаге вычислений: Xn+1=02 –02–0,5219= – 0,5219; Yn+1=2·0·0+0,4999.
Теперь полагаем Xn = Xn+1 = – 0,5219; Yn = Yn+1 = 0,4999, и по формулам (1) получаем на втором шаге: Xn+1 = (–0,5219)2 – (0,4999)2 – 0,5219 = – 0,4994...;
Yn+1 = 2·(–0,5219)·(0,4999) + 0,4999 = – 0,0218....
Затем полагаем Xn = Xn+1 = – 0,4994...; Yn = Yn+1 = –0,0218, и опять по формулам (1) продолжаем дальше. То есть на каждом последующем шаге вычислений (итераций) предыдущие значения Xn+1 и Yn+1 надо подставлять в формулы (1) в качестве новых значение Xn и Yn.
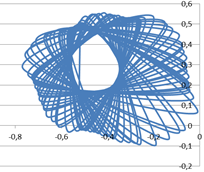
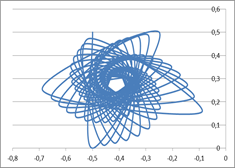
В программе « Microsoft Excel» можно сделать 32000 подобных «шагов»-вычислений, а затем построить («точками») график функции Yn+1 = f(Xn+1), который и будет похож на «пылающее солнце». Более того, меняя числовые значения параметров p и q, на том же графике можно увидеть и другие объекты; например, при p = – 0,5; q = 0,4999 вместо «солнца» получится «спиральная галактика».
Представлю алгоритм, который я составила, для построения в программе «Microsoft Excel» фракталов Мандельброта «пылающее солнце» и «спиральная галактика». На практике для достижения приемлемой точности достаточно 100 итераций.
Таблица 1.
Алгоритм построения в программе “Microsoft Excel” фрактала Мандельброта «пылающее солнце» (для 100 итераций)
|
1.Записать в ячейку А1 переменную Xn 2.Записать в ячейку В1 переменную Yn. 3.Записать в ячейку D1 параметр р. 4.Записать в ячейку E1 параметр q. 5.Записать в ячейку G1 переменную Xn+1. 6.Записать в ячейку H1 переменную Yn+1. 7.Ввести в ячейку А2 значение 0. 8.Ввести в ячейку В2 значение 0. 9.Ввести в ячейку А3 формулу =G2. 10.Ввести в ячейку В3 формулу =H2. 11.Ввести в ячейку D2 значение -0,5219. |
|
|
12.Ввести в ячейку E2 значение 0,4999. 13.Ввести в ячейку G2 формулу =A2^2-B2^2+$D$2 14.Ввести в ячейку H2 формулу =2*A2*B2+$E$2 15.Растянуть ячейку А3 за правый нижний уголок до A101. 16.Растянуть ячейку В3 за правый нижний уголок до B101. 17.Растянуть ячейку G2 за правый нижний уголок до G101. 18.Растянуть ячейку H2 за правый нижний уголок до H101. 19.Выделить область значений от G2 до H101. 20.Для построения фигуры сделать следующее: Вставка->Диаграммы->Точечная->Точечная с гладкими кривыми |
|
Таблица 2.
Алгоритм построения в программе “Microsoft Excel” фрактала Мандельброта «спиральная галактика» (для 100 итераций)
|
1.Записать в ячейку А1 переменную Xn 2.Записать в ячейку В1 переменную Yn. 3.Записать в ячейку D1 параметр р. 4.Записать в ячейку E1 параметр q. 5.Записать в ячейку G1 переменную Xn+1. 6.Записать в ячейку H1 переменную Yn+1. 7.Ввести в ячейку А2 значение 0. 8.Ввести в ячейку В2 значение 0. . 9.Ввести в ячейку А3 формулу =G2. |
|
|
10.Ввести в ячейку В3 формулу =H2. 11.Ввести в ячейку D2 значение -0,5. 12.Ввести в ячейку E2 значение 0,4999. 13.Ввести в ячейку G2 формулу =A2^2-B2^2+$D$2 14.Ввести в ячейку H2 формулу =2*A2*B2+$E$2 15.Растянуть ячейку А3 за правый нижний уголок до A101. 16.Растянуть ячейку В3 за правый нижний уголок до B101. 17.Растянуть ячейку G2 за правый нижний уголок до G101. 18.Растянуть ячейку H2 за правый нижний уголок до H101. 19.Выделить область значений от G2 до H101. 20.Для построения фигуры сделать следующее: Вставка->Диаграммы->Точечная->Точечная с гладкими кривыми |
|
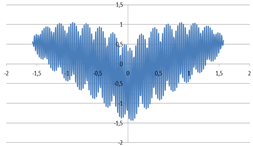
Рассмотрим фрактал «кривая Гильберта», заданный формулой (2):
y (x) = (cos0,5x ⋅ cos 200x + |x|0,5 − 0,7)(4 − x2)0,01. Найдем область допустих значений данного выражения. Под арифметическим квадратным корнем находится функция cos(x), значит, cos(x) ≥ 0.
Представлю алгоритм, который я составила, для построения в программе “Microsoft Excel” фрактала «кривая Гильберта» по данной формуле (2) в допустимой области значений, выбрав шаг равный 0,01.
Таблица 3.
Алгоритм построения в программе “Microsoft Excel” фрактала «кривая Гильберта»
|
1.Записать в ячейку A1 переменную х. 2.Записать в ячейку B1 переменную у. 3.Записать в ячейку A2 значение -π/2, согласно области допустимых значений XЄ[-π/2; π/2], 4.Ввести в ячейку A3 формулу =A2+0,01. |
|
|
5.Растянуть ячейку А3 за правый нижний уголок до ячейки А316 (до значения 1,57). 6.Ввести в ячейку В2 формулу =((КОРЕНЬ(COS(A2)))*COS(200*A2)+КОРЕНЬ(ABS(A2))-0,7)*(4-A2*A2)^0,01 7.Растянуть ячейку В2 за правый нижний уголок до ячейки В316. 8.Выделить область значений от А2 до В316. 9.Для построения фигуры сделать следующее: Вставка->Диаграммы->Точечная->Точечная с гладкими кривыми |
|
Рассмотрим фрактал Мандельброта «кривая Дракона», заданный системами уравнений (3) и (4) соответственно:
![]()
![]()
Сначала полагаем Xn = 0; Yn = 0. Задаем случайным образом параметр m, который меняется от 0 до 1. Если m > 0,5, то применяем систему уравнений (3) для построения фрактала, иначе — (4). Каждое новое значение получается из предыдущего в зависимости от случайного числа.
Представлю алгоритм, который я составила, для построения в программе “Microsoft Excel” фрактала Мандельброта «кривая Дракона».
Таблица 4.
Алгоритм построения в программе “Microsoft Excel” фрактала Мандельброта «кривая Дракона»
|
1. Записать в ячейку А1 номер n. 2. Записать в ячейку В1 случайную величину m. 3. В ячейку С1 записать х. 4. В ячейку D1 записать у. 5. В ячейку А2 записать 1. |
|
|
6. В ячейку А3 ввести формулу =A2+1 7. Растянуть А3 до ячейки А 11363 8. В ячейку В2 записать функцию случайного числа =СЛЧИС() 9. Растянуть ячейку В2 до В 11363 10. Ввести в ячейку С2 значение 0 11. Ввести в ячейку С3 формулу =ЕСЛИ(B3>0,5;-0,4*C2-1;0,76*C2-0,4*D2) 12. Растянуть ячейку С3 до ячейки С 11363 13. Ввести в ячейку D2 значение 0. 14. Ввести в ячейку D3 формулу =ЕСЛИ(B3>0,5;-0,4*D2+0,1;0,4*C2+0,76*D2) 15. Растянуть ячейку D3 до ячейки D11363 16. Выделить ячейки от С2 до D11363 17. Для построения фигуры сделать следующее: Вставка->Диаграммы->Точечная |
|
Заключение
Компьютер можно характеризовать как новое средство познания. Благодаря ему, можно увидеть связи и значения, которые до сих пор были скрыты от нас.
Выполняя исследовательскую работу, я убедилась в том, что область применения фракталов чрезвычайно велика. Их помощь необходима, например, когда требуется задать линии и поверхности очень сложной формы с помощью нескольких коэффициентов.
Можно сказать, что фактически найден способ легкого, удобного представления сложных неевклидовых объектов, образы которых похожи на природные.
Фракталы позволяют посмотреть на математику совсем с другой стороны, открывают нам глаза. Казалось бы, производятся обычные расчёты с обычными цифрами, однако это даёт нам по-своему уникальные, неповторимые результаты, которые позволяют почувствовать себя творцом природы. Фракталы дают понять, что математика — это тоже наука о прекрасном.
Список литературы:
1.Бенуа Мандельброта. «The Fractal Geometry of Nature», 1977.
2.Мандельброт Б. Фрактальная геометрия природы. М.: Институт компьютерных исследований, 2002. — 656 с.
3.Морозов А.Д. Введение в теорию фракталов. Москва-Ижевск: Институт компьютерных исследований, 2002. — 160 с.
4.О фракталах. [Электронный ресурс] — Режим доступа. — URL: http://elementy.ru/posters/fractals
5.Перерва Л.М., Юдин В.В. П 27 Фрактальное моделирование: учебное пособие / под общ. ред. В.Н. Гряника. Владивосток: Изд-во ВГУЭС, 2007. — 186 с.
дипломов



Оставить комментарий