ПРИМЕНЕНИЕ  ТЕОРИИ  ГРАФОВ  В  КОДИРОВАНИИ  И  ДЕКОДИРОВАНИИ  ИНФОРМАЦИИ

Васильева  Марина  Владимировна

студент  3  курса,  факультет  информатики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

E -mail:  vasmarishka1994@mail.ru

Додонова  Наталья  Леонидовна

научный  руководитель,  канд.  физ.-мат.  наук,  доцент,  кафедра  прикладной  математики  СГАУ  им.  академика  С.П.  Королева,  РФ,  г.  Самара

В  последние  годы  особую  важность  приобрели  те  разделы  математики,  которые  имеют  отношение  к  развитию  цифровых  устройств,  цифровой  связи  и  цифровых  вычислительных  машин.  Базой  для  преподавания  этих  дисциплин  наряду  с  классическими  методами  анализа  непрерывных  физических  моделей  стали  алгебраические,  логические  и  комбинаторные  методы  исследования  различных  моделей  дискретной  математики.

Значительно  возросла  популярность  теории  графов  —  ветви  дискретной  математики.

Теория  графов  стала  мощным  средством  исследования  и  решения  многих  задач,  возникающих  при  решении  больших,  сложных  систем.

Действительно,  существует  ряд  систем,  изучение  которых  становится  значительно  проще  с  использованием  теории  графов.  Кроме  того  теория  графов  оказалась  полезной  при  изучении  задач,  возникающих  в  некоторых  областях  наук,  таких  как,  теории  групп,  теории  матриц,  теории  информации.

В  настоящее  время,  с  развитием  научно-технического  прогресса,  изучение  теории  графов  обрело  актуальность  в  связи  с  применением  при  разработке  эффективных  алгоритмов  оптимизации  тех  или  иных  процессов.

В  настоящее  время  теория  графов  охватывает  большой  материал  и  активно  развивается.

Цель  работы:  с  помощью  теории  графов  закодировать  и  декодировать  информацию.

Задачи  работы:  рассмотреть  основные  понятия  из  теории  графов,  изучить  алгоритм  Хаффмана  для  кодирования  и  декодирования  информации,  построить  кодовое  дерево.

Основные  понятия  из  теории  графов

Граф  —  это  средство  для  наглядного  представления  состава  и  структуры  системы.  Граф  состоит  из  вершин,  связанных  дугами  или  ребрами.  Вершины  могут  быть  изображены  кругами,  овалами,  точками,  прямоугольниками  и  пр.  Связи  между  вершинами  изображаются  линиями  —  ребрами.  Если  линия  направленная  (т.е.  со  стрелкой),  то  она  называется  дугой,  если  не  направленная,  то  такой  граф  называется  ориентированным  графом.  Две  вершины,  соединенные  дугой  или  ребром,  называются  смежными.

Взвешенный  (размеченный)  граф  —  это  граф,  в  котором  с  вершинами  или  линиями  связана  дополнительная  информация.  Эта  информация  называется  весом  вершины  или  линии.  Вес  позволяет  отобразить  на  графе  не  только  структуру  системы,  но  и  различные  свойства  компонент  и  связей,  количественные  характеристики  и  пр.

Семантическая  сеть  —  модель  знаний  в  форме  графа.  В  основе  таких  моделей  лежит  идея  о  том,  что  любые  знания  можно  представить  в  виде  совокупности  объектов  (понятий)  и  связей  (отношений)  между  ними.

Связным  называется  граф,  в  котором  любые  две  вершины  можно  соединить  непрерывным  путем,  сопоставленным  из  нескольких  ребер  графа.

Граф,  не  содержащий  циклов,  называется  ациклическим.

Связный  ациклический  граф  называется  деревом  (свободным  деревом). 

Основные  свойства  деревьев  в  виде  теоремы:

Теорема.  Для  графа  G  следующие  утверждения  эквивалентны: 

1.  G  —  дерево;

2.  Любые  две  вершины  в  графе  G  соединены  единственной  простой  цепью;

3.  G  —  связный  граф  и  p=q+1;

4.  G  —  ациклический  граф  и  p=q+1;

5.  G  —  ациклический  граф,  и  если  любую  пару  несмежных  вершин  соединить  ребром  х,  то  в  графе  G+х  будет  точно  один  цикл; 

6.  G  —  связный  граф,  отличный  от  Кр  для  р=3,  и  если  любую  пару  несмежных  вершин  соединить  ребром  х,  то  в  графе  G+х  будет  точно  один  цикл; 

7.  G  —  граф,  отличный  от  и,  p=q+1,  и  если  любую  пару  несмежных  вершин  соединить  ребром  х,  то  в  графе  G+х  будет  точно  один  цикл.

Любое  из  утверждений  теоремы  можно  использовать  в  качестве  определения  дерева.

Дерево  —  граф,  обладающий  следующими  свойствами:

·     ни  в  один  из  углов  не  входит  более  одной  дуги;

·     только  в  один  узел  (он  называется  корнем)  не  входит  ни  одной  дуги;

·     перемещаясь  от  корня  по  дугам,  можно  попасть  в  любой  узел.

Неориентированное  дерево  (или  просто  дерево)  —  это  конечный  связный  граф  с  выделенной  вершиной  (корнем)  без  циклов.  Дерево  не  имеет  петель  и  кратных  рёбер.

Дерево  и  названо  дерево,  поскольку,  будучи  нарисованным,  выглядит  как  дерево,  только  перевёрнутое  «вверх  ногами».  Граф,  изображённый  на  рисунке  1,  является  примером  дерева.

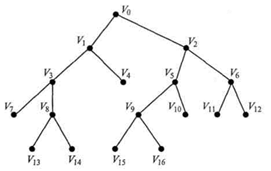
Рисунок  1.  Дерево

Для  каждой  пары  вершин  дерева  —  узлов  —  существует  единственный  маршрут,  поэтому  вершины  удобно  классифицировать  по  степени  удалённости  от  корневой  вершины.

Упорядоченным  деревом  называется  дерево,  в  котором  поддеревья  каждого  узла  образуют  упорядоченное  подмножество.

В  информатике  принято  использовать  подмножество  множества  деревьев,  когда  каждый  узел  либо  является  листом,  либо  образует  два  поддерева:  левое  и  правое.  Такой  вид  деревьев  называется  бинарными  деревьями  и  используется  при  делении  множества  на  два  взаимоисключающих  подмножества  по  какому-то  признаку.

На  рисунке  2  приведен  пример  упорядоченного  дерева  и  соответствующего  ему  бинарного.

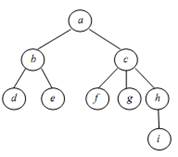
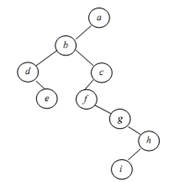
Рисунок  2.  Упорядоченное  дерево  и  соответствующее  ему  бинарное

Лист  дерева  —  это  узел,  из  которого  не  выходит  ни  одной  дуги.  Два  листа,  имеющие  общий  узел,  называются  родственными.

Двоичное  дерево  —  дерево,  у  которого  из  каждого  угла  выходит  только  две  дуги.

H-дерево  —  двоичное  дерево  кодирования,  у  которого  каждый  узел  имеет  вес,  причем  вес  родителя  равен  сумме  весов  детей.

Применение  теории  графов

Графы  широко  используются  в  различных  отраслях  науки.

Двоичные  кодовые  деревья  допускают  интерпретацию  в  рамках  теории  поиска.  Каждой  вершине  при  этом  сопоставляется  вопрос,  ответить  на  который  можно  либо  «да»,  либо  «нет».  Утвердительному  и  отрицательному  ответу  соответствуют  два  ребра,  выходящие  из  вершины.  «Опрос»  завершается,  когда  удается  установить  то,  что  требовалось. 

Двоичные  деревья  играют  весьма  важную  роль  в  теории  информации.  Предположим,  что  определенное  число  сообщений  требуется  закодировать  в  виде  конечных  последовательностей  различной  длины,  состоящих  из  нулей  и  единиц.  Если  вероятности  кодовых  слов  заданы,  то  наилучшим  считается  код,  в  котором  средняя  длина  слов  минимальна  по  сравнению  с  прочими  распределениями  вероятности.  Задачу  о  построении  такого  оптимального  кода  позволяет  решить  алгоритм  Хаффмана.

Алгоритм  Хаффмана

Алгоритм  Хаффмана  —  адаптивный  алгоритм  оптимального  префиксного  кодирования  алфавита  с  минимальной  избыточностью.

Этот  алгоритм  был  разработан  1952  году  аспирантом  Массачусетского  технологического  института  Дэвидом  Хаффманом  при  написании  им  курсовой  работы.  В  настоящее  время  используется  во  многих  программах  сжатия  данных.

Сжатие  информации  —  проблема,  имеющая  достаточно  давнюю  историю,  гораздо  более  давнюю,  нежели  история  развития  вычислительной  техники,  которая  (история)  обычно  шла  параллельно  с  историей  развития  проблемы  кодирования  и  шифровки  информации.

Все  алгоритмы  сжатия  оперируют  входным  потоком  информации,  минимальной  единицей  которой  является  бит,  а  максимальной  –  несколько  бит,  байт  или  несколько  байт.

Целью  процесса  сжатия,  как  правило,  есть  получение  более  компактного  выходного  потока  информационных  единиц  из  некоторого  изначально  некомпактного  входного  потока  при  помощи  некоторого  их  преобразования.

Метод  сжатия  информации  на  основе  двоичных  кодирующих  деревьев  был  предложен  Д.А.  Хаффманом.  Кодирование  Хаффмана  является  простым  алгоритмом  для  построения  кодов  переменной  длины,  имеющих  минимальную  среднюю  длину.

Кодирование  —  это  преобразование  сообщений  в  сигнал,  т.  е.  преобразование  сообщений  в  кодовые  комбинации.

Идея  алгоритма  кодирования:  зная  вероятность  вхождения  символов  (частоту  встречаемости  символа  в  сообщении),  можно  описать  процедуру  построения  кодов  переменной.  Символу,  имеющему  большую  вероятность,  присваиваются  более  короткие  коды.

Классический  алгоритм  Хаффмана  имеет  на  входе  таблицу  частот  появления  символов  и,  зная  ее  основание,  строится  так  называемое  дерево  Хаффмана.

Символы  входного  алфавита  образуют  список  свободных  узлов.

Каждый  лист  имеет  вес,  который  равен  либо  вероятности,  либо  количеству  вхождений  символа  в  сжимаемое  сообщение.

Обратным  процессом  кодирования  является  декодирование  .

Пусть  дана  частота  встречаемости  каждого  символа  в  сообщении  или  дано  дерево  Хаффмана  и  некоторая  битовая  последовательность,  полученная  с  его  помощью,  как  описано  в  предыдущем  пункте.  Для  получения  текста  по  этой  последовательности  следует  многократно  повторять  траверс  от  корня  к  листьям,  перемещаясь  в  левое  поддерево,  если  встречен  0,  и  в  правое  поддерево,  если  1.  Каждый  раз  по  достижению  листа  символ  в  нём  следует  добавлять  в  полученный  текст  и  снова  начинать  процедуру  от  корня,  продолжая  просмотр  последовательности  с  того  же  места.

Рассмотрю  данный  алгоритм  Хаффмана  на  придуманных  мною  задачах.

Задача  №  1.  Закодировать  по  методу  Хаффмана  сообщение:

Самарский  государственный  аэрокосмический  университет

Решение:

1.  Посчитаю  количество  символов  в  данном  сообщении  Q  =  53

2.  Найду  частоты  появления  (вероятности)  символов  и  занесу  их  в  таблицу  1.

Таблица  1.

Таблица  частот  появления  символов

3.  Кодируемые  знаки  расположу  в  порядке  убывания  их  вероятностей  (р_i)

4.  На  каждом  шаге  две  последние  позиции  списка  (жирным  шрифтом)  суммирую  и  заменяю  одной  (выделенной  цветом),  которой  приписываю  данный  результат  сложения.  Далее  вновь  сортирую  список  вероятностей,  при  этом  сохраняю  информацию  о  том,  какие  именно  символы  объединялись  на  каждом  этапе.  Процесс  продолжаю  до  тех  пор,  пока  не  останется  единственная  позиция,  вероятность  которой  равна  1.

Таблица  2.

Алгоритм  Хаффмана

5.  Строю  кодовое  дерево.  Корню  дерева  ставлю  узел,  вероятность  которого  равна  1.  Затем  каждому  узлу  приписываю  два  потомка  с  вероятностями,  которые  участвовали  в  образовании  значения  вероятности  этого  узла. 

6.  Данный  процесс  продолжаю  до  достижения  узлов,  соответствующих  вероятностям  исходных  знаков.

Одной  из  ветвей,  выходящей  из  каждого  узла,  например,  с  меньшей  вероятностью,  ставлю  в  соответствие  символ  0,  а  с  большей  —  1.  Спускаюсь  от  корня  к  нужному  символу  и,  тем  самым,  получаю  код  этого  символа. 

Таким  образом,  получаю  кодовое  дерево  (см.  Приложение  1).

Составлю  таблицу  соответствия  символов  с  полученным  кодом  Хаффмана:

Таблица  3.

Таблица  соответствия  символов  с  полученным  кодом  Хаффмана

Чтобы  убедиться  в  том,  что  исходное  сообщение  сжалось,  сравню  объемы  данного  сообщения,  закодированного  с  помощью  ASCII-кодов  и  закодированного  с  помощью  алгоритма  Хаффмана.

Рассчитаю  объем  сообщения  после  кодирования  кодом  Хаффмана:  суммирую  произведение  частоты  встречаемости  символа  и  количества  0  и  1  соответствующее  этому  символу  по  коду  Хаффмана.

I₁=6*3+5*3+4*4+4*4+4*4+3*4+3*4+3*4+3*4+3*4+3*4+2*5+2*5+2*5+1*6+1*6+1*6+1*6+1*6+1*6  =  18+15+48+72+30+36  =  219  бит

Сообщение  в  памяти  компьютера  закодировано  с  помощью  ASCII-кодов,  каждый  символ  весит  8  бит.  Значит,  объем  исходного  сообщения  найду  по  формуле:

I  =  K*i,

где:  K  —  количество  символов  в  сообщении, 

i  —  вес  одного  символа  в  битах,

I  —  информационный  объем  данного  сообщения.

В  моей  задаче  K  =  53,  i  =  8  бит,  значит,  I₂  =  8*53  =  424  бит

Коэффициент  сжатия:

k  =  I₂/I₁

k=

Ответ:  закодированное  данное  сообщение  методом  Хаффмана  выглядит  так:  110001101111101101110101000011000001001011100000100100111001100111011101010001111111111010110011011001000100101101111110110100100001101001001110100011110011011000011000001001011110001100001111111011010100000011111010111

Декодирование

Рассмотрю  на  следующем  примере,  как  происходит  процесс  декодирования. 

Задача  №  2.  Дано  дерево  Хаффмана  (см.  Приложение  2)  и  битовая  последовательность  (закодированное  сообщение):

010010011011100010000011011111111000011010110111001000101011111001000111010110100110010111011101100010001111010000

Получить  исходное  сообщение  (раскодировать).

Решение:

Для  получения  текста  по  этой  последовательности  многократно  повторяю  траверс  от  корня  к  листьям,  перемещаясь  в  левое  поддерево,  если  встречен  1,  и  в  правое  поддерево,  если  0.  Каждый  раз  по  достижению  листа  символ  в  нём  добавляю  в  полученный  текст  и  снова  начинаю  процедуру  от  корня,  продолжая  просмотр  последовательности  с  того  же  места.

Ответ:  Математика  —  царица  всех  наук.

Заключение

В  работе  я  рассмотрела  основные  понятия  теории  графов,  виды  графов.  Описала  алгоритм  Хаффмана,  метод  сжатия  информации,  кодирования  и  декодирования. 

Применяя  теорию  графов  и  используя  алгоритм  Хаффмана,  закодировала  и  декодировала  информацию,  построив  кодовое  дерево.

С  помощью  графов  решать  задачи  очень  удобно,  интересно,  увлекательно.  Теория  графов  обеспечивает  эффективное  сжатие  информации.