Статья опубликована в рамках: XXIX Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 февраля 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ИМИТАЦИОННАЯ МОДЕЛЬ МАР-ПОТОКА СОБЫТИЙ В УСЛОВИЯХ НЕПРОДЛЕВАЮЩЕГОСЯ ЭКСПОНЕНЦИАЛЬНОГО МЕРТВОГО ВРЕМЕНИ
Березин Дмитрий Владимирович
магистрант 1 курса, кафедра исследования операций ТГУ, РФ, г. Томск
Е-mail : berezin14@mail.ru
Нежельская Людмила Алексеевна
научный руководитель, канд. техн. наук, доцент ТГУ, РФ, г. Томск
1. Введение
С развитием техники возникли новые задачи, требующие решения. Например, обслуживание заявок, поступающих на телефонную станцию или билетную кассу. Как оказалось, подобные задачи возникают во многих направлениях исследований: технике, экономике, транспорте. Теория, изучающая задачи данного типа, называется теорией массового обслуживания.
Основные элементы и методы исследования теории массового обслуживания можно найти в книгах Б.В. Гнеденко, И.Н. Коваленко [1].
В реальных ситуациях часто приходится сталкиваться с тем, что параметры входящих потоков и обслуживающих приборов неизвестны или частично известны, кроме того, могут изменяться со временем. При этом изменения обычно носят случайный характер, что приводит к рассмотрению дважды стохастических потоков событий. Двойная случайность заключается в следующем: во-первых, моменты наступления событий случайны, во-вторых, интенсивность потока есть случайный процесс. Более того, встречаются ситуации, когда не все моменты наступления событий наблюдаемы. Это может происходить по многим причинам. Одной из таких причин является период ненаблюдаемости, порождаемый зарегистрированным событием, получивший название «мертвое время».
Потоки событий с интенсивностью, зависящей от времени можно разделить на два класса. К первому классу относятся потоки с интенсивностью, которая является непрерывным случайным процессом. Ко второму классу относятся потоки, у которых интенсивность есть кусочно-постоянный случайный процесс с конечным числом состояний. Такие потоки получили название MC-потоки (Markov chain). MC-потоки являются хорошей математической моделью телекоммуникационных сетей. Зачастую реальные информационные потоки аппроксимируются MC-потоками с числом состояний большим двух [2], но исследование дважды стохастических потоков с двумя состояниями также имеет большое значение. MC-потоки возможно представить в виде моделей MAP-потоков событий (Markovian Arrival Process) [3].
2. Постановка задачи
Рассмотрим поток событий с интенсивностью, представляющей собой ненаблюдаемый кусочно-постоянный случайный процесс ![]() с двумя состояниями
с двумя состояниями ![]() и
и ![]() (
(![]() ).
).
Длительность пребывания процесса ![]() в каждом состоянии есть случайная величина с функцией распределения
в каждом состоянии есть случайная величина с функцией распределения ![]() ,
, ![]() .
.
Пусть в момент времени ![]() имеет место первое состояние процесса
имеет место первое состояние процесса ![]() . В момент окончания состояния возможны 3 ситуации:
. В момент окончания состояния возможны 3 ситуации:
1) Процесс остается в первом состоянии и наступает событие потока. Вероятность этой ситуации ![]() .
.
2) Процесс переходит из первого состояния во второе и наступает событие потока. Вероятность этой ситуации ![]() .
.
3) Процесс переходит из первого состояния во второе и событие потока не наступает. Вероятность этой ситуации ![]() .
.
При этом ![]() .
.
Аналогично для второго состояния процесса ![]() .
.
Матрица инфинитезимальных характеристик примет блочный вид:
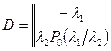

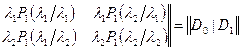 .
.
Элементами матрицы ![]() являются интенсивности переходов процесса
являются интенсивности переходов процесса ![]() из состояния в состояние с наступлением события. Недиагональным элементам матрицы
из состояния в состояние с наступлением события. Недиагональным элементам матрицы ![]() соответствуют интенсивности переходов из состояния в состояние без наступления события.
соответствуют интенсивности переходов из состояния в состояние без наступления события.
Описанный выше поток носит название MAP-потока событий [3].
Рассмотрим ситуацию, когда не все события являются наблюдаемыми. После каждого зарегистрированного события наступает время случайной длительности ![]() , в течение которого поток ненаблюдаем (мертвое время). Длительность мертвого времени есть случайная величина с функцией распределения
, в течение которого поток ненаблюдаем (мертвое время). Длительность мертвого времени есть случайная величина с функцией распределения ![]() . События, наступившие в течение мертвого времени, теряются, не продлевая его длительность, т. е.
. События, наступившие в течение мертвого времени, теряются, не продлевая его длительность, т. е. ![]() — непродлевающееся мертвое время. Далее, новое зарегистрированное событие снова порождает период ненаблюдаемости случайной длительности.
— непродлевающееся мертвое время. Далее, новое зарегистрированное событие снова порождает период ненаблюдаемости случайной длительности.
На рисунке 1 приведен пример возникающей ситуации. Здесь ![]() и
и ![]() — значения состояний ненаблюдаемого процесса
— значения состояний ненаблюдаемого процесса ![]() ,
, ![]() — моменты наступления событий в наблюдаемом потоке,
— моменты наступления событий в наблюдаемом потоке, ![]() — длительность мертвого времени после
— длительность мертвого времени после ![]() -го зарегистрированного события.
-го зарегистрированного события.

Рисунок 1. Формирование наблюдаемого потока событий
Задача заключается в построении имитационной модели MAP-потока событий в условиях непродлевающегося мертвого времени.
3. Имитационное моделирование
Задача построения имитационной модели сводится к задаче генерации значений ![]() случайной величины — времени пребывания процесса
случайной величины — времени пребывания процесса ![]() в
в ![]() -м состоянии,
-м состоянии, ![]() . Длительность пребывания процесса
. Длительность пребывания процесса ![]() в
в ![]() -м состоянии имеет плотность распределения вероятностей
-м состоянии имеет плотность распределения вероятностей ![]() и функцию распределения
и функцию распределения ![]() ,
, ![]() . В соответствии с методом обратных функций [4] обозначим
. В соответствии с методом обратных функций [4] обозначим ![]() . Тогда имеем
. Тогда имеем ![]() , откуда находим
, откуда находим ![]() — значение экспоненциально распределенной случайной величины – времени пребывания процесса
— значение экспоненциально распределенной случайной величины – времени пребывания процесса ![]() в
в ![]() -м состоянии,
-м состоянии, ![]() , а
, а ![]() есть значение случайной величины
есть значение случайной величины ![]() , равномерно распределенной на отрезке
, равномерно распределенной на отрезке ![]() [4].
[4].

Рисунок 2. Процесс ![]()
Так как длительность мертвого времени также экспоненциально распределенная случайная величина, то для генерации ее значений, согласно методу обратных функций, будем иметь формулу ![]() .
.
4. Результаты
Результаты работы модели приведены ниже. Для первого эксперимента были использованы исходные данные, приведенные в таблице 1.
Таблица 1.
Исходные данные для первого эксперимента
|
|
|
|
|
|
|
|
|
|
|
|
Результаты первого эксперимента приведены в таблице 2.
Таблица 2.
Результаты первого эксперимента
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
1.597 |
1.777 |
2.854 |
… |
6.072 |
7.158 |
7.329 |
7.676 |
9.048 |
9.521 |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
1.597 |
1.777 |
2.854 |
… |
6.072 |
|
7.329 |
|
9.048 |
9.521 |
|
|
0.098 |
0.544 |
0.237 |
… |
1.151 |
|
1.393 |
|
0.088 |
0.137 |
Здесь ![]() — моменты наступления событий MAP-потока,
— моменты наступления событий MAP-потока, ![]() — состояние процесса
— состояние процесса ![]() , в котором наступило событие MAP-потока (условимся, что сначала наступает событие, затем процесс
, в котором наступило событие MAP-потока (условимся, что сначала наступает событие, затем процесс ![]() переходит из состояния в состояние),
переходит из состояния в состояние), ![]() — моменты наступления событий в наблюдаемом потоке,
— моменты наступления событий в наблюдаемом потоке, ![]() — длительность мертвого времени после зарегистрированного события
— длительность мертвого времени после зарегистрированного события
Для второго эксперимента уменьшим параметр ![]() . Как известно, математическое ожидание экспоненциальной случайной величины с функцией распределения
. Как известно, математическое ожидание экспоненциальной случайной величины с функцией распределения ![]() равно
равно ![]() . Таким образом, уменьшая
. Таким образом, уменьшая ![]() , можем ожидать, что увеличится средняя длительность мертвого времени. Исходные данные для второго эксперимента приведены в таблице 3.
, можем ожидать, что увеличится средняя длительность мертвого времени. Исходные данные для второго эксперимента приведены в таблице 3.
Таблица 3.
Исходные данные для второго эксперимента
|
|
|
|
|
|
|
|
|
|
|
|
Результаты второго эксперимента продемонстрированы в таблице 4.
Таблица 4.
Результаты второго эксперимента
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.207 |
1.681 |
2.109 |
2.842 |
3.098 |
5.261 |
5.564 |
5.984 |
8.097 |
8.945 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.207 |
|
|
2.842 |
|
5.261 |
|
5.984 |
|
|
|
|
0.930 |
|
|
2.253 |
|
0.666 |
|
6.045 |
|
|
Как и ожидалось, во втором эксперименте событий наблюдаемого потока наступило значительно меньше, чем в MAP-потоке, и меньше по сравнению с первым экспериментом, т. к. был уменьшен параметр ![]() .
.
5. Заключение
В данной работе описан MAP-поток событий с двумя состояниями, получена основная формула для построения имитационной модели MAP-потока, приведены численные результаты экспериментов. Таким образом, сравнивая начальные данные и значения, приведенные в таблицах, можно сделать вывод об адекватности работы построенной модели.
Список литературы:
1.Гнеденко Б.В. Введение в теорию массового обслуживания / Б.В. Гнеденко, И.Н. Коваленко. М.: Наука, 1966. — Гл. 1 : Задачи теории массового обслуживания в простейших предпосылках. — С. 12—91.
2.Горцев А.М. Оптимальная оценка состояний асинхронного дважды стохастического потока событий с произвольным числом состояний / А.М. Горцев, В.Л. Зуевич Вестн. Томского гос. ун-та. Сер. Управление, выч. техника и информатика. — 2010. — № 2 (11). — С. 44—65.
3.Горцев А.М. Математическое моделирование: о связи MC-потоков и MAP-потоков событий / А.М. Горцев, Л.А. Нежельская. Вестн. Томского гос. ун-та. Сер. Управление, выч. техника и информатика. — 2011. — № 1. — С. 13—21.
4.Соболь И.М. Численные методы Монте-Карло / И.М. Соболь. М.: Наука, 1973. — 311 с.
отправлен участнику


Оставить комментарий