АНАЛИЗ  КАЧЕСТВЕННЫХ  ХАРАКТЕРИСТИК  СТРОИТЕЛЬНЫХ  МАТЕРИАЛОВ  МЕТОДОМ  МАТЕМАТИЧЕСКОГО  ПЛАНИРОВАНИЯ  ЭКСПЕРИМЕНТА

Мурсалова  Диана  Рашидовна

студент  1  курса,  кафедра  строительства  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

E -mail:  diankamur@mail.ru

Тимофеева  Елена  Фёдоровна

научный  руководитель,  канд.  физ.-мат.  наук,  доцент  кафедры  высшей  алгебры  и  геометрии  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

Первостепенную  роль  в  повышении  эффективности  строительных  работ  играет  контроль  за  их  качеством.  В  перечень  главных  задач  контроля  входят:  профилактика,  обнаружение,  а  также  ликвидация  отклонений  от  нормы,  способных  привести  к  производственному  браку  в  области  строительства,  которая  является  одной  из  самых  материалоёмких  отраслей  народного  хозяйства.  Именно  поэтому  достижение  высокой  продуктивности  строительно-монтажных  работ  тесно  связано  с  качеством  используемых  материалов.

Таким  образом,  контроль  качества  изделий,  как  при  их  изготовлении,  так  и  при  применении,  —  обязательный  компонент  в  строительной  индустрии.  Основной  целью  такого  контроля  является  неукоснительное  следование  проектным  решениям,  осуществление  работ  в  соответствии  с  требованиями  строительных  норм  и  правил,  государственных  стандартов,  а  также  использование  материалов  и  изделий  согласно  технологиям  и  предписаниям  заводов-изготовителей.

Строительные  материалы  и  изделия  характеризуются  основными  свойствами,  которые  являются  наиболее  важными  при  их  применении.  В  свою  очередь,  функциональные  свойства,  например  такие,  как  прочность,  деформативность,  теплопроводность,  а  также  надёжность  строительных  материалов  определяются  их  физико-химическими  свойствами,  к  которым  относятся  средняя,  истинная  и  насыпная  плотности,  морозостойкость,  пористость,  водопоглощение,  стойкость  к  влиянию  агрессивных  сред,  объёмная  масса  и  многие  другие  характеристики.

Анализ  качества  материалов  проводится  на  основании  результатов  испытаний  стандартных  образцов  на  те  или  иные  воздействия.  Так  как  минимальное  число  образцов,  определённое  ГОСТом,  чаще  всего  не  превышает  пяти,  то  интервальная  оценка  данных,  полученных  в  ходе  экспериментов,  не  применима,  не  может  быть  выявлен  и  закон  распределения  случайных  величин,  средние  значения  и  дисперсия  которых  также  не  являются  объективными.
В  связи  с  этим  предлагается  использовать  основанный  на  теории  возможностей  метод  оценки  качества  строительной  продукции.  В  отличие  от  вероятностных  методов  выдвигается  предположение  о  применимости  возможностей,  а  не  вероятностей  законов  распределения.

В  строительной  сфере  нередко  используется  экспоненциальная  модель  функции  распределения  возможностей,  которая  выглядит  следующим  образом:

,

где:    и    —  параметры  распределения,  рассчитываемые  по  нижеприведённым  формулам:

,

,

,  ,

где:  ,    —  соответственно  наибольшее  и  наименьшее  значения  измеряемого  параметра;

  —  уровень  риска,  значением  которого  задаются  в  соответствии  со  степенью  ответственности  эксплуатируемой  конструкции,  а  также  с  числом  и  точностью  измеряемых  параметров.

Графически  функция  распределения  возможностей  фактически  представлена  в  виде  трёх  функций.  Функция    представляет  собой  возможность  реализации  события  ;  функция    служит  для  описания  противоположного  события  (в  теории  возможностей  );  функция    называется  необходимостью  события  ,  при  этом  .  Следовательно,  случайное  событие  может  быть  описано  двумя  функциями    и  ,  причём  описание  события  определяется  интервалом  [N;R].

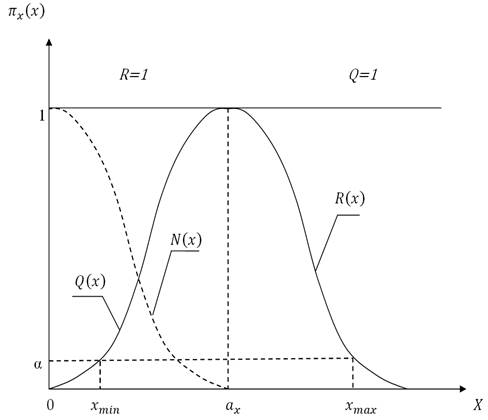
Рисунок  1.  Функция  распределения  возможностей

Значения  элементов  нечёткого  множества  ,  например  результаты  лабораторных  испытаний  образцов,  обозначим  следующим  образом:

.

В  качестве  примера  рассмотрим  определение  прочности  древесины  маньчжурского  ясеня  по  результатам  испытаний  пяти  образцов  при  сжатии  вдоль  волокон.  Сопротивление  данному  виду  сжатия,  являющемуся  одним  из  важных  механических  свойств  древесины,  составляет  значительную  величину,  колеблющуюся  у  различных  пород  от  35  до  60  МПа  при  стандартной  влажности  12  %.  Предположим,  что  в  ходе  испытаний  были  получены  следующие  результаты:    МПа.  Пусть  ,  тогда:

Экспоненциальная  функция  распределения  возможностей  будет  выглядеть  так:

Зададимся  следующим  вопросом:  может  ли  прочность  древесины  быть  равной  42  МПа?  Пусть    МПа.  Так  как  ,  то  возможность  того,  что  прочность  древесины  окажется  равной  42  МПа,  равна  1.  Необходимость    МПа  определяется  из  выражения  ,  где    —  возможность  того,  что  прочность  древесины  не  равна  42  МПа. 

Величину    при    МПа  можно  определить  следующим  образом:

Следовательно,  ,  .  Исходя  из  полученных  данных,  можно  сделать  следующий  вывод:  возможность  того,  что  прочность  древесины  равна  42  МПа  находится  в  интервале  .  Если  нижнее  значение  обеспеченности  исследуемой  величины  не  вызывает  уверенности  для  принятия  необходимого  решения,  то  следует  в  качестве    принять  следующее  меньшее  значение  изучаемого  параметра.  В  нашем  случае  предположим,  что  прочность  древесины  равна  41  МПа.  Используя  формулу  функции  распределения  возможностей,  получим:

Следовательно,  возможность  того,  что  прочность  древесины  равна  41  МПа,  находится  в  интервале  .  Если  произвести  аналогичные  расчёты,  приняв    МПа,  то  получим  интервал  .  Таким  образом,  значение  прочности  древесины  маньчжурского  ясеня,  равное  40  МПа,  обладает  наибольшей  гарантией  обеспеченности  по  сравнению  с  другими.

Если  в  качестве  оценки  возможной  прочности  древесины  использовать  вероятностный  метод  расчётов,  получим  следующие  величины:

Средние  значения  величины  :

Среднее  квадратичное  отклонение:

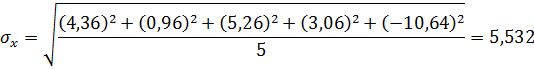
Предположим,  что  закон  распределения  результатов  испытаний  нормальный,  тогда  приблизительно  с  вероятностью,  равной  0,9973,  по  правилу  трёх  сигм  получим,  что  практически  все  значения  нормально  распределённой  случайной  величины  лежат  в  следующем  интервале: 

.

Следовательно,  прочность  древесины  с  обеспеченностью  0,9973  можно  принять  равной:

  МПа

Сравнивая  этот  результат  с  тем,  который  был  получен  при  использовании  метода  оценки  данных,  основанного  на  теории  возможностей,  можно  убедиться  в  несостоятельности  применения  вероятностных  методов  при  оценке  качества.

Методика  анализа  качественных  характеристик  строительных  материалов  с  использованием  модели  функции  распределения  возможностей  была  многократно  проверена  экспериментально  и  может  успешно  использоваться  на  практике  при  малом  количестве  результатов  испытаний.

Список  литературы:

1.Галаева  Н.Л.  Определение  надежности  элементов  по  критерию  прочности  при  вероятностных  и  возможностных  базовых  параметрах  в  математической  модели  предельного  состояния  /  Н.Л.  Галаева,  В.С.  Уткин,  О.С.  Плотникова  //  Известия  ОрелГТУ.  —  2007.  —  №  4.  —  С.  86—90.

2.Горев  В.В.  Математическое  моделирование  при  расчетах  и  исследовании  строительных  конструкций:  Учеб.  пособие  /  В.В.  Горев,  В.В.  Филиппов,  Н.Ю.  Тезиков.  М.:  Высш.  шк.,  2002.  —  206  с.

3.Красовский  П.С.  Исследование  и  оптимизация  свойств  строительных  материалов  с  применением  элементов  математической  статистики.  .Хабаровск:  Издательство  ДВГУПС,  2004.  —  128  с.

4.Пытьев  Ю.П.  Возможность  как  альтернатива  вероятности.  Математические  и  эмпирические  основы,  применение.  М.:ФИЗМАТЛИТ,  2007.  —  464  с.

5.Уткин  В.С.  Оценка  качества  строительных  материалов  при  малом  числе  образцов  //  Строительные  материалы.  —  2001.  —  №  1.  —  С.  32—33.

6.Уткин  В.С.  Расчёт  надёжности  грунтового  основания  фундамента  по  несущей  способности  (сдвигу)  на  стадии  эксплуатации  //  Инженерно-строительный  журнал.  —  2014.  —  №  1.  —  С.  92—93.