АНАЛИЗ  И  СТАТИСТИЧЕСКАЯ  ОБРАБОТКА  РЕЗУЛЬТАТОВ  ИССЛЕДОВАНИЙ  В  ОПРЕДЕЛЕНИИ  НЕКОТОРЫХ  СВОЙСТВ  БЕТОНА

Мухамеджанова  Лилия  Вильдановна

студент  1  курса,  кафедра  строительства  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

E -mail:  liliya22.1995@gmail.com

Григорян  Лусине  Арсеновна

научный  руководитель,  старший  преподаватель  кафедры  высшей  алгебры  и  геометрии  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

Строительные  материалы,  каждые  из  которых  имеют  определённые  характеристики,  подбираются,  исходя  из  назначения  зданий,  а  также  условий  эксплуатации  сооружений.

Одним  из  самых  важных  строительных  материалов,  который  известен  вот  уже  более  шести  тысяч  лет,  является  бетон.  Он  представляет  собой  один  из  сложнейших  искусственных  материалов,  получающихся  в  процессе  формирования,  а  впоследствии  застывания  определённо  подобранной  смеси,  состоящей  из  вяжущего  вещества,  в  основном  цемента,  и  других  заполнителей,  чаще  воды. 

Малая  энергоёмкость,  экологическая  безопасность,  сравнительно  неограниченная  сырьевая  база,  а  также  простота  и  доступность  технологии  изготовления  позволяют  применять  бетон  в  различных  эксплуатационных  условиях.

Данный  материал,  позволивший  в  значительной  степени  повысить  производительность  труда,  сократить  расход  древесины  и  других  традиционных  строительных  материалов,  а  также  уменьшить  сроки  возведения  зданий,  обладает  рядом  уникальных  свойств,  в  числе  которых  прочность,  пористость,  теплопроводность,  морозостойкость,  проницаемость  и  другие.

Качество  бетона  главным  образом  определяется  показателем  его  средней  прочности  и  однородности,  оцениваемой  согласно  коэффициенту  прочностной  вариации.  Однако  невозможно  оценить  качество  данного  строительного  материала,  руководствуясь  только  лишь  значением  его  средней  прочности,  так  как  на  практике  эта  величина  зачастую  отклоняется  от  теоретически  рассчитанной.  Также  колебания  активности  бетонной  смеси,  её  минералогического  состава,  нормальной  густоты,  режимов  перемешивания  составляющих  и  их  твердения,  приводят  к  неоднородности  структуры  бетона,  вследствие  чего  отдельные  объёмы  этого  материала  могут  в  большей  или  меньшей  степени  отличаться  друг  от  друга,  а  значит,  будут  колебаться  и  показатели  свойств  бетона.

Для  оценки  однородности  бетона  используют  статистические  методы  расчётов.  Рассмотрим  определение  однородности  бетона  в  случае  растяжения  при  изгибе  балок,  изготовленных  из  этого  материала,  с  размерами  202060  см.  Исходные  значения  прочности  бетона,  полученные  в  ходе  экспериментальных  исследований,  преобразуем  в  вариационный  ряд,  располагая  их  в  порядке  возрастания:

3,83;  3,84  3,90;  3,91;  3,95;  3,96;  4,00;  4,03;  4,05;  4,07;  4,15;  4,20;  4,49;  4,51;  4,55;  4,59;  4,63;  4,63;  4,64;  4,70;  4,75;  4,79;  4,83;  4,84;  4,84;  4,88;  4,92;  4,94;  4,96;  5,01;  5,11;  5,25;  5,39;  5,41;  5,51;  5,60;  5,75;  5,79.

Определяем  число  групп  по  формуле  Стерджесса:

,

где    —  объем  испытаний.

Осуществив  соответствующее  действие,  имеем  .  Принимаем  в  качестве    ближайшее  целое  к  рассчитанному  по  формуле  значение,  таким  образом  получаем,  что  .

Определяем  шаг  интервала:

В  формуле    и    —  крайние  члены  вариационного  ряда,  соответственно  равные  максимальному  и  минимальному  значениям  исследуемой  величины.

Определяем  границы  интервалов:

-  3,83  …  (3,83  +)=4,11

-  4,11  …  4,39

-  4,39  …  4,67

-  4,67  …  4,95

-  4,95  …  5,23

-  5,23  …  5,51

-  5,51  …  5,79

Таблица  1.

Интервальный  вариационный  ряд

—  интервальная  частота  (относительная),  определяемая  для  k-ого  интервала  по  исходному  вариационному  ряду  с  учетом  его  границ;

—  относительная  частота

,

  —  накопленная  частота,  которая  вычисляется  по  следующей  формуле:

Вычисляем  оценки  числовых  характеристик:

Математическое  ожидание:

Среднеквадратическое  отклонение:

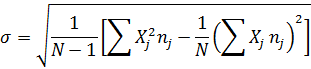
Коэффициент  вариации:

Проверку  однородности  результатов  наблюдения  проводим  при  помощи  критерия  Ирвина:

где:    и    —  последний  (максимальное  значение)  и  предпоследний  члены  исходного  вариационного  ряда;

  и    —  первый  (минимальное  значение)  и  второй  члены  вариационного  ряда;

  —  критическое  значение  критерия  Ирвина.

Следовательно,  результаты  экспериментальных  исследований    и    —  однородны.

Таким  образом,  в  процессе  выполнения  расчетов  было  установлено,  что  результаты  лабораторных  испытаний  балок  из  бетона  202060  см  на  растяжение  при  изгибе  являются  однородными. 

Методы  математического  планирования  эксперимента  могут  быть  применены  при  обработке  результатов  лабораторных  и  натурных  экспериментов  различных  строительных  материалов  и  конструкций,  а  также  могут  помочь  при  оптимизации  их  свойств.

Таким  образом,  на  примере  определения  однородности  балок  из  бетона,  мы  убедились  в  том,  что  применение  математической  статистики  в  строительстве  позволяет  облегчить  проверку  соответствия  используемых  строительных  материалов  требованиям  проекта.

Список  литературы:

1.Алимов  Л.А.,  Баженов  Ю.М.,  Воронин  В.В.,  Магдеев  У.Х.  Технология  бетона,  строительных  изделий  и  конструкций.  Москва:  Издательство  АСВ,  2004.  —  256  с.

2.Гмурман  В.Е.  Теория  вероятностей  и  математической  статистике:  Учеб.пособие  /  В.Е.  Гмурман.  М.:  Юрайт,  2013.  —  478  с.

3.Красовский  П.С.  Исследование  и  оптимизация  свойств  строительных  материалов  с  применением  элементов  математической  статистики.  .Хабаровск:  Издательство  ДВГУПС,  2004.  —  128  с.