АНАЛИЗ  ЗАВИСИМОСТИ  ПРОЧНОСТИ  ЗАТВЕРДЕВАНИЯ  СТРОИТЕЛЬНОГО  ГИПСА  ОТ  ОБЪЁМНОЙ  КОНЦЕНТРАЦИИ  ТВЁРДОЙ  ФАЗЫ  С  ПОМОЩЬЮ  МЕТОДОВ  МАТЕМАТИЧЕСКОГО  ПЛАНИРОВАНИЯ  ЭКСПЕРИМЕНТА

Голдобина  Лилия  Владимировна

студент  1  курса,  кафедра  строительства  СКФУ,  РФ,  г.  Ставрополь

E-mail: 

Тимофеева  Елена  Фёдоровна

научный  руководитель,  канд.  физ.-мат.  наук,  доцент  СКФУ,  РФ,  г.  Ставрополь

Изучение  свойств  строительных  материалов  —  та  сфера  деятельности,  в  которой  проводится  большое  количество  экспериментов  для  получения  зависимости  этих  свойств  от  различных  факторов  (температуры,  времени  и  т.  д.).  Может  случиться,  что  такая  зависимость  выражается  формулой,  выведенной  теоретически.  Но  во  многих  случаях  такая  формула  неизвестна  и  зависимость  между  величинами  устанавливается  на  основе  полученных  результатов  измерений  путём  аналитического  поиска  вида  функции,  приближенно  выражающей  её.

Использование  методов  математического  планирования  для  установления  зависимости  между  случайными  величинами,  полученными  в  результате  эксперимента,  имеет  важное  практическое  значение.  Наиболее  эффективными  методами  для  достижения  этой  цели  являются  метод  наименьших  квадратов  и  метод  нахождения  уравнения  линейной  регрессии.

В  данной  статье  эти  методы  будут  использоваться  для  исследования  зависимости  прочности  затвердевания  строительного  гипса  от  объёмной  концентрации  твёрдой  фазы  через  2  часов  и  7  суток  твердения. 

Строительный  гипс  находит  применение  среди  современных  строительных  и  отделочных  материалов  и  используется  главным  образом  для  производства  гипсовых  и  гипсобетонных  изделий,  применяемых  во  внутренних  частях  зданий.  Для  получения  прочных  изделий  необходимо  повышать  прочность  строительного  гипса.  Для  этого  выявив  закономерность  между  исследуемыми  величинами  можно  будет  сделать  вывод  о  том,  каким  образом  лучше  повышать  прочность  материала. 

По  методу  наименьших  квадратов  проведём  вычисления  линейного  приближения.  Пусть  прочность  затвердевания  ,  время  твердения  2  часа,  объёмная  концентрация  твёрдой  фазы,  приближающая  функция    и  известны  результаты  измерений:

Таблица  1.

Экспериментальные  данные  для  проведения  исследования

Составим  систему  уравнений,  из  которой  найдём  коэффициенты  :

Результаты  промежуточных  вычислений  сведём  в  таблицу  2.

Таблица  2.

Промежуточные  расчёты

Решив  данную  систему  уравнений  получим:

Таким  образом,  зависимость  имеет  вид: 

Построим  график  функции  и  в  той  же  системе  координат  график  по  исследуемым  точкам  (рис.  1).

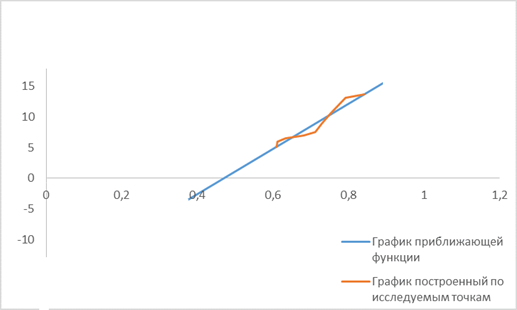
Рисунок  1.  Графики  аналитической  и  экспериментальной  зависимостей  между  прочностью  затвердевания  и  объёмной  концентрацией  твёрдой  фазы  после  2  часов  твердения

После  2  часов  твердения  гипс  представляет  собой  твёрдую  систему,  но  не  обладает  окончательной  кристаллизацией.  Это  является  причиной  того,  что  график,  построенный  по  исследуемым  точкам,  только  приближается  к  линейной  зависимости.

На  основе  тех  же  данных  найдём  уравнение  линейной  регрессии,  которое  имеет  вид:

Коэффициенты    и    найдём  по  формулам:

Подставив  значения,  получим:

Таким  образом,  уравнение  линейной  регрессии  будет  иметь  вид:

Используя  два  различных  метода  математического  планирования  эксперимента  мы  получили  приблизительно  одинаковые  уравнения.  На  их  основе  можно  сделать  вывод  о  приближении  к  линейной  зависимости  прочности  затвердевания  гипса  от  объёмной  концентрации  твёрдой  фазы.  К  двум  часам  твердения  гипс  обладает  хорошо  развитой  кристаллизационной  структурой,  о  чем  можно  судить  по  ее  прочности,  однако  процессы  гидратации  к  этому  сроку  в  твердеющей  системе  еще  не  завершаются.  В  период  до  7  суток  твердения  происходит  превращение  конденсационной  структуры  в  кристаллизационную,  которой  свойственна  достаточно  высокая  прочность.  Поэтому  аналогичные  расчёты  проводим  для  исследования  зависимости  через  7  суток  твердения.

Полученные  результаты  измерений:

Таблица  3.

Экспериментальные  данные  для  проведения  исследования

Результаты  промежуточных  вычислений  сведём  в  таблицу  4.

Таблица  4.

Промежуточные  расчёты

Составим  систему  уравнений  и,  решив  ее,  получаем:

Решив  данную  систему  уравнений  получим:

Таким  образом,  зависимость  имеет  вид: 

Построим  график  функции  и  в  той  же  системе  координат  график  по  исследуемым  точкам  (рис.  2).

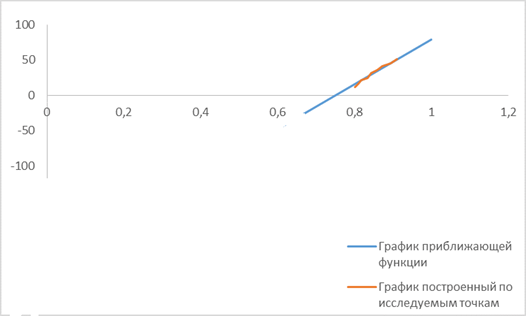
Рисунок  2.  Графики  аналитической  и  экспериментальной  зависимостей  между  прочностью  затвердевания  и  объёмной  концентрацией  твёрдой  фазы  после  7  суток  твердения

После  7  суток  твердения  гипс  окончательно  кристаллизован,  в  результате  чего  график  сглаживается  и  зависимость  между  прочностью  затвердевания  и  объёмной  концентрацией  твёрдой  фазы  является  линейной.

Составим  уравнение  линейной  регрессии:

Уравнение  линейной  регрессии  будет  иметь  вид:

Как  и  в  предыдущем  случае,  используя  два  различных  метода  математического  планирования  эксперимента,  мы  получили  приблизительно  одинаковые  уравнения  зависимости  между  исследуемыми  величинами.

В  результате  проведённых  вычислений,  можно  сделать  вывод  о  том,  что  независимо  от  времени  твердения  зависимость  между  прочностью  затвердевания  строительного  гипса  и  объёмной  концентрацией  твёрдой  фазы  является  линейной.  Для  получения  прочных  изделий  из  строительного  гипса  его  необходимо  предварительно  уплотнить  для  увеличения  объёмной  концентрации  твёрдой  фазы  и  как  следствие  прочности  материала.  Таким  образом,  использование  методов  математического  планирования  эксперимента  в  строительстве  позволяет  установить  вид  зависимости  между  исследуемыми  величинами  и  сделать  важные  с  практической  точки  зрения  выводы.

Список  литературы:

1.Красовский  П.С.  Исследование  и  оптимизация  свойств  строительных  материалов  с  применением  элементов  математической  статистики:  учебное  пособие  /  Красовский  П.С.  М.:  Издательство  ДВГУПС,  2004.  —  128  с. 

2.Лотов  В.А.  Влияние  объемной  концентрации  полуводного  гипса  на  прочность  гипсовых  изделий  /  Лотов  В.А.  //  Строительные  материалы.  —  2001.  —  №  1.  —  С.  28—30.

3.Письменный  Д.Т.  Конспект  лекций  по  теории  вероятностей,  математической  статистике  и  случайным  процессам  /  Письменный  Д.Т.  3-е  изд.  М.:  Айрис-пресс,  2008.  —  288  с.