РЕШЕНИЕ  УРАВНЕНИЙ  ЧЕТВЕРТОЙ  СТЕПЕНИ  СПОСОБОМ  ДЕКАРТА-ЭЙЛЕРА

Фомин  Александр  Владимирович

студент  2  курса,  отделение  информационных  технологий,  Колледж  электроники  и  бизнеса  ОГУ,  РФ,  г.  Оренбург

E-mail:  f

Нурманова  Сабиля  Андреевна

научный  руководитель,  преподаватель  I   кв.  категории  предметно-цикловой  комиссии  физико-математических  дисциплин,  Колледж  электроники  и  бизнеса  ОГУ,  РФ,  г.  Оренбург

Решение  уравнений  четвертой  степени  способом  Декарта-Эйлера.

Рассмотрим  неполное  уравнение  четвертой  степени

  х⁴  +  рх²+  qx  +  r  =  0  (1)

с  произвольными  комплексными  коэффициентами  р,  q,  r. 

Пусть  х₁,  х₂,  x₃,х₄  —  его  корни.  По  формулам  Виета,

х₁  +  х₂  +  x₃  +  х₄  =  0,

  х₁  х₂  +  х₁  х₃  +  х₁  х₄  +  х₂  х₃  +  х₂  х₄  +  х₃  х₄  =  p  (2)

х₂х₃х₄  +  х₁х₃х₄  +  х₁х₂х₄  +  х₁х₂х₃  =  –  q,

х₁х₂х₃х₄  =  r.

Числа  х₁х₂  +  х₃х₄  ,  х₁х₃  +  х₂  х₄  и  х₁х₄  +  х₂х₃  являются  корнями  кубического  уравнения 

  х³  –  px²  –  4rx  +  (4pr  –  q²)  =  0  (3)

Заметим,  что 

х₁х₂  +  х₃х₄  =   (х₁  +  х₂  –  x₃  –  х₄)²  –    (х₁  +  х₂  +  x₃  +  х₄)²  +  (х₁х₂  +  х₁  х₃  +  х₁  х₄  +

+  х₂  х₃  +  х₂  х₄  +  х₃  х₄)  =    (х₁  +  х₂  –  x₃  –  х₄)²  +  p.

Аналогично

х₁х₃  +  х₂  х₄  =    (х₁  –  х₂  +  x₃  –  х₄)²  +  p,

х₁х₄  +  х₂  х₃  =    (х₁  –  х₂  –  x₃  +  х₄)²  +  p.

Поэтому,  если  мы  сделаем  в  уравнении  (3)  замену  х  =  у  +  р,  то  полученное  уравнение 

  у³  +  2 pу²+  (p²—  4r)у  —  q²  =  0  (4)

будет  иметь  своими  корнями  числа

y ₁  =    (х₁  +  х₂  –  x₃  –  х₄)²,

y ₂  =    (х₁  –  х₂  +  x₃  –  х₄)²,  (5)

y ₃  =    (х₁  –  х₂  –  x₃  +  х₄)².

Из  формул  (5)  получаем,  что

  (х₁  +  х₂  –  x₃  –  х₄)²  =  u_1,

(х₁  –  х₂  +  x₃  –  х₄)²  =  u_2,  (6)

  (х₁  –  х₂  –  x₃  +  х₄)²  =  u_3,

где  u_1,  u_2,  u₃  —  квадратные  корни  из  y₁,  y_2,  y₃.

Поскольку  квадратный  корень  из  комплексного  числа  имеет  два  значения,  необходимо  уточнить,  какие  значения  квадратных  корней  следует  взять  в  формулах  (7). 

Пусть  дано  тождество

(х₁  +  х₂  –  x₃  –  х₄)  (х₁  –  х₂  +  x₃  –  х₄)  (х₁  –  х₂  –  x₃  +  х₄)  =    –  4  σ  ₁  σ  ₂  +  8  σ  ₃,

где  ơ₁,  ơ₂,  ơ₃  —  элементарные  симметрические  многочлены  от  х₁,  х₂,  х₃,  х₄.  Для  корней  уравнения  (1)  имеем,  в  силу  формул  (2): 

(х₁  +  х₂  –  x₃  –  х₄)  (х₁  –  х₂  +  x₃  –  х₄)  (х₁  –  х₂  –  x₃  +  х₄)  =  8q.

Отсюда  следует,  что 

  u₁,  u₂,  u₃  =  –  q.  (7)

Условие  (7)  оставляет  четыре  из  восьми  вариантов  выбора  значений  квадратных  корней  из  y₁,  y₂,  у₃.  Любой  из  этих  четырех  вариантов  допустим,  так  как,  перенумеровав  подходящим  образом  х₁,  х₂,  х₃,  х₄,  можно  умножить  на  (–  1)  любые  два  из  выражений  х₁  +  х₂  –  x₃  –  х₄,  х₁  –  х₂  +  x₃  –  х₄,  х₁  –  х₂  –  x₃  +  х₄,  не  изменив  третьего.  Например,  если  поменять  номера  у  х₁  и  х₂  и  одновременно  у  х₃  и  х₄,  то  выражение  х₁  +  х₂  –  x₃  –  х₄  не  изменится,  в  то  время  как  остальные  два  умножатся  на  (–  1).  Складывая  равенства  (6)  и  равенство  х₁  +  х₂  +  x₃  +  х₄  =  0,  находим:  x₁  (u₁  +  u₂  –  u₃). 

Аналогично  находим:

x ₂  (u₁  –  u₂  –  u₃),

x ₃  (–  u₁  +  u₂  –  u₃),

x ₄    (–  u₁  –  u₂  +  u₃).

Эти  формулы  можно  объединить  в  одну:

  x  =    (  +    +  ),  (8)

которую  следует  понимать  таким  образом,  что  значения  квадратных  корней  выбираются  всеми  возможными  способами,  лишь  бы  их  произведение  равнялось  (–  q). 

Подставляя  полученную  формулу  в  выражения  для  корней  кубического  уравнения  (3),  найденные  при  помощи  формулы  Кардано,  можно  получить  явную  формулу,  выражающую  корни  уравнения  (1)  через  его  коэффициенты,  которая,  однако,  столь  громоздка,  что  выписывать  ее  не  имеет  смысла. 

Пример.  Решите  уравнение  на  множестве  действительных  чисел 

Решение.  Поставим  задачу  привести  это  уравнение  к  виду 

Для  этого  воспользуемся  подстановкой    получим:

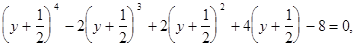
,  откуда  находим  ,  ,  .

,

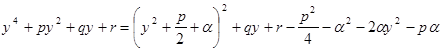или

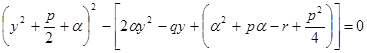
Подберем    так,  чтобы  квадратный  трехчлен,  стоящий  в  скобках,  стал  полным  квадратом,  чтобы  затем  получить  разность  квадратов  двух  выражений. 

Для  этого  его  дискриминант  должен  быть  равен  нулю

Мы  получили  кубическое  уравнение  относительно  .  Решение  кубических  уравнений  по  формуле  Кардано  нам  уже  известно.

Положим    тогда  кубическое  уравнение  примет  вид:

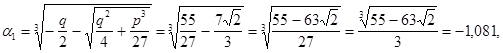
Ответ: 

Список  литературы:

1.Винберг  Э.Б.  Алгебра  многочленов:  учебное  пособие  для  студентов  заочников  III—IV  курсов  физико-математических  факультетов  педагогических  институтов.  М.:  Просвещение,  1980.  —  175  с.

2.Курош  А.Г.  Алгебраические  уравнения  произвольных  степеней.  М.:  Наука,  1975.  —  34  с.

3.Мишина  А.П,  Проскуряков  И.А.  Высшая  алгебра.  Линейная  алгебра,  многочлены,  общая  алгебра.  М.:  Наука,  1980.  —  563  с.

4.Сушкевич  А.К.  Основы  высшей  алгебры.  М.:  ОГИЗ,  1941.  —  462  с.

5.Туманов  С.И.  Поиски  решения  задачи.  М.:  Просвещение,  1969.  —  275  с.

6.Тишин  В.И.  Математика  для  учителей  и  учащихся:  рациональные  алгебраические  уравнения.  М.:  Комаричи,  2002.  —  166  с.