ОПТИМИЗАЦИЯ  РАСКРОЯ  ЛИСТОВОГО  МАТЕРИАЛА  НА  ПРЯМОУГОЛЬНИКИ  РАЗЛИЧНЫХ  РАЗМЕРОВ

Гиниатуллина  Регина  Айратовна

студент  1  курса  магистратуры,  кафедра  прикладной  математики  и  информатики  КНИТУ  им.  А.Н.  Туполева,  РФ,  г.  Казань

E-mail:  regina1402@yandex.ru

Галиев  Шамиль  Ибрагимович

научный  руководитель,  д-р  техн.  наук,  профессорИТКиИ  КНИТУ  им.  А.Н.  Туполева,  РФ,  г.  Казань

Гильотинный  раскрой  стальных  и  иных  листов  широко  используется  в  машиностроении  и  других  отраслях  промышленности.  Этот  раскрой  фактически  является  задачей  упаковки  квадратов  различных  размеров  в  заданный  лист  при  использовании  гильотинной  процедуры.  При  этом  важно  уменьшить  отходы  листа.  Интерес  к  задачам  упаковки  объясняется  их  большой  практической  значимостью.  Как  правило,  такие  задачи  относятся  к  материалоемким  производствам,  где  одним  из  основных  факторов  снижения  себестоимости  выпускаемой  продукции  является  рациональное  использование  ресурсов.  Данная  задача  имеет  широкий  спектр  практических  приложений  в  тех  отраслях  индустрии,  где  традиционно  возникают  задачи  упаковки  (раскроя)  в  машиностроении,  деревообработке,  лёгкой  и  строительной  индустрии.

1.  Обзор  по  задаче

В  промышленности  при  изготовлении  различных  видов  конечной  продукций  возникает  задача  оптимального  раскроя  листов  заданных  размеров  на  прямоугольные  заготовки.  Эта  задача  состоит  в  следующем:  известны  размеры  квадратов,  размер  листа.  Требуется  разместить  в  лист  заданные  квадраты  без  перекрытия  друг  с  другом  так,  чтобы  можно  было  кроить  лист  гильотиной.  Под  гильотинным  понимается  раскрой,  реализуемый  последовательностью  сквозных  резов,  параллельных  кромкам  материала.  Кроме  того,  эти  квадраты  должны  быть  ортогонально  упакованными  без  вращений,  то  есть  у  каждого  выбранного  элемента  типа  ,  сторона  с  высотой    должна  быть  параллельна  стороне  листа  с  высотой  H.  Мы  будем  рассматривать  проблему  упаковки  квадратов  разного  размера  в  прямоугольник.  Решим  эту  проблему  с  помощью  одного  точного  алгоритма.  Он  основан  на  итеративном  выполнении  рекурсивной  процедурой  алгоритма  ветвей  —  и  —  границ  (его  мы  так  же  рассмотрим)  с  различными  входными  параметрами,  чтобы  определить  оптимальное  значение  решения.

2.  Цель  проекта

Цель  данной  работы  состоит  в  исследовании  и  реализации  алгоритма,  способного  находить  решения  упаковки  квадратов  в  прямоугольник.  Рассматриваемая  задача  имеет  широкое  применение  в  различных  отраслях  промышленности:  машиностроении,  деревообработке,  лёгкой  и  строительной  индустрии.

Необходимо  осуществить  возможность  вывода  на  экран  полученного  результата  в  виде  вписанных  в  прямоугольник  квадратов  различного  размера  и  соответствующей  дополнительной  информации,  необходимой  пользователю.  Например,  такой  как:  времени  работы  алгоритма,  различных  сведений  об  ошибках  и  т.  д.

3.  Общие  требования

1)  Задание  вручную  размеров  прямоугольника-листа  (ширины  и  высоты),  в  который  будут  упаковываться  квадраты;

2)  Ручной  ввод  размеров  квадратов  (они  могут  быть  как  одинаковыми,  так  и  различными);

3)  Визуальный  просмотр  результатов  выполнения  алгоритма  (с  выводом  соответствующей  информации:  время  выполнения  алгоритма,  количества  квадратов  определенного  размера  вписавшихся  в  прямоугольник);

4)  Сохранение  в  файл  информацию  об  уже  вписанных  квадратах.

4.  Актуальность  проблемы

Основной  целью  проектируемой  системы  является  соответствие  основному  алгоритму  упаковки  квадратов  и  удобство  эксплуатации  конечным  пользователем,  отказоустойчивость.

Задачи  и  функции  проектируемой  системы  должны  соответствовать  поставленным  требованиям.

Предложенный  в  данной  работе  алгоритм  может  быть  использован  для  эффективного  решения  задачи  упаковки  квадратов  в  прямоугольную  область  заданных  размеров.  Данная  задача  имеет  широкий  спектр  практических  приложений  в  тех  отраслях  индустрии,  где  традиционно  возникают  задачи  раскроя-упаковки.  Рассмотренный  алгоритм  можно  использовать  в  практических  расчетах  и  включать  его  в  автоматизированные  системы  проектирования  и  управления.  Можно  также  сказать,  что  проблема  является  актуальной  на  данный  момент,  так  как  есть  потребность  в  упаковке  квадратов  в  прямоугольник  и  эта  потребность  никогда  не  закончится,  а  значит  и  проблема  будет  актуальной  всегда. 

Задачи  раскроя-упаковки  занимают  важное  место  в  современной  комбинаторной  оптимизации  и  привлекают  внимание  многих  ученых,  как  в  России,  так  и  за  рубежом.

Интерес  к  задачам  раскроя-упаковки  объясняется,  в  частности,  их  большой  практической  значимостью.  Как  правило,  приложения  задач  раскроя-упаковки  относятся  к  материалоемким  производствам,  где  одним  из  основных  факторов  снижения  себестоимости  выпускаемой  продукции  является  рациональное  использование  ресурсов.

5.  Существующие  системы  раскроя.

Существуют  много  программных  продуктов  для  раскроя  листового  материала,  такие  как  ORION,  АСТРА  РАСКРОЙ,  ТЕХТРАН  [1].  Рассмотрим  один  из  них  на  примере  ТЕХТРАНА. 

Для  предприятий,  использующих  машины  термической  резки,  внедрение  современных  информационных  технологий  —  задача  из  числа  самых  актуальных.  Понятно,  что  сокращение  сроков  подготовки  программ  раскроя,  оптимальное  размещение  деталей  на  листе,  меньший  расход  материала  решающим  образом  повлияют  на  себестоимость  и  качество  продукции.

Новый  программный  продукт  Техтран/Раскрой  дополняет  линейку  программ  семейства  Техтран  и  предназначен  для  проектирования  программ  раскроя  листового  материала.  Возможности  CAM-системы  объединены  здесь  с  функциями  организации  производственного  процесса.  Подход  к  решению,  использованный  в  программе,  суммирует  опыт  работы  ряда  предприятий,  эксплуатирующих  машины  термической  резки.  Задача  в  том,  чтобы  по  заданию  на  раскрой,  которое  состоит  из  номенклатуры  отобранных  деталей  и  их  количества  по  каждому  наименованию,  оперативно,  учитывая  складские  запасы,  оптимальным  образом  разложить  детали  на  листах  и  получить  управляющие  программы  резки  этих  деталей.  Листы  делового  отхода,  остающиеся  после  работы,  должны  быть  учтены  в  базе  данных  системы  для  дальнейшего  использования.

6.  Формализация  задачи  и  разработка  математической  модели

Приведем  математическую  модель  задачи,  следуя  работе  [5].

Алгоритм  ветвей  —  и  —  границ  основан  на  модели  целочисленного  линейного  программирования  (ЦЛП).  Ради  простоты  в  этой  формулировке  мы  полагаем,  что  каждый  элемент  отличен,  то  есть  для  каждого  типа  j  прямоугольников  ,  мы  определяем    идентичных  элементов,  имеющих  ширину  ,  высоту    и  выгоду  .  Пусть 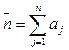   (1)  будет  общим  количеством  элементов.  Для  каждого  элемента  k  вводим  бинарную  переменную    принимающую  значение  1  тогда  и  только  тогда,  когда  элемент  k  включен  в  оптимальное  решение.  Модель  ЦЛП  для  общей  двумерной  задачи  рюкзака  выглядит  следующим  образом:

где:    —  размеры  вписанного  квадрата, 

—  размеры  самого  прямоугольника, 

U   —  любая  верхняя  граница  величины  оптимального  решения  и  C  обозначает  множество  всех  подмножеств    элементов,  которые  не  могут  быть  упакованы  в  лист  гильотинным  способом.  Для  величины  порога  U  мы  используем  ,  то  есть,  величину  оптимального  решения  для  двумерной  задачи  рюкзака,  соответствующей  упрощению,  согласно  которому  ограничения  гильотинности  опущены.  Отметим,  что  ограничения  (3)  и  (4)  избыточны,  но  добавлены  к  формулировке,  чтобы  усилить  его.  Наш  алгоритм  решает  упрощенную  задачу,  в  которой  ограничения  (5)  устранены  и  проверено  будет  ли  текущее  решение  допустимо  или  нет  с  помощью  решения  следующей  задачи  разделения:  будут  ли  все  элементы  из    вписываться  в  лист  при  гильотинном  подходе?  В  случае,  если  ответ  положителен,  то  оптимальное  решение  общей  двумерной  задачи  рюкзака  найдено.  Иначе,  находится  новое  нарушенное  ограничение,  и  процесс  повторяется.

Этот  подход  подобен  методу,  предложенному  Капрара  и  Монаси  [2]  для  точного  решения  двумерной  задачи  рюкзака  и  согласно  Пизингеру  и  Сигарду  [6]  для  того,  чтобы  решить  саму  общую  двумерную  задачу  рюкзака.  Более  точно,  модель  (2)—(6)  решена  специализированным  методом  ветвей  и  границ,  в  котором  элементы  упорядочены.  Верхние  границы  получаются  из  ЛП  релаксации  задачи  (2)—(3)  с  использованием  верхней  границы    Мартелло  и  Тота  [5].  Обратный  проход  происходит  всякий  раз,  когда  верхняя  граница  не  превышает  текущее  решение,  или  когда  некоторые  ограничения  (3)—(5)  нарушены.

В  задаче  2—6  не  учтено,  что  раскрой  гильотинный.  С  учетом  всех  условий  рассматриваем  рекурсивный  метод  решения.

7.  Метод  решения

В  этом  пункте  мы  рассмотрим  рекурсивную  процедуру  для  перечисления  гильотинных  двумерных  упаковок.  В  процедуре,  называемой  рекурсивной,  мы  обозначим  каждое  допустимое  расположение  подмножества  элементов  на  листе  как  допустимую  упаковку.  Каждая  допустимая  упаковка  может  быть  представлена  как  неотрицательный  целочисленный  вектор  ,  где  каждая  координата    представляет  число  элементов  типа    в  упаковке.  Обозначим  как    прибыль  упаковки  .  Мы  говорим,  что  допустимая  упаковка    максимальна,  если  никакие  дальнейшие  элементы  не  могут  быть  упакованы  в  лист,  то  есть,  упаковка    оказывается,  неосуществимой  для  всех  типов    элементов,  таким  образом,  что  .  Для  двух  допустимых  упаковок    и    мы  определяем  новую  упаковку  следующим  образом:  ,  .

Рекурсивная  процедура  неявно  перечисляет  все  допустимые  упаковки,  рекурсивно  деля  лист  на  две  части  посредством  (горизонтального  либо  вертикального)  гильотинного  реза.  Процедура  получает  во  входе  параметр  ,  который  является  нижней  границей  прибыли  любой  допустимой  (гильотинной)  упаковки. 

Как  замечено  Кристодесом  и  Уитлогом  [3],  для  любой  задачи  двумерной  упаковки  существует  оптимальное  решение,  соответствующее  нормальному  образцу,  то  есть,  решение,  в  котором  для  любого  упакованного  элемента  его  левая  сторона  прилегает  либо  к  правой  стороне  другого  элемента  или  правой  стороне  листа.  Это  означает,  что  мы  можем  рассмотреть  только  вертикальные  разрезы,  по  координатам  ,  которые  могут  быть  получены  как  комбинация  ширин  элементов,  то  есть,  которые  принадлежат  множеству:

Похожим  способом  мы  рассматриваем  только  горизонтальные  разрезы,  по  координатам ,  принадлежащих  следующему  множеству:

Мы  предполагаем,  что  элементы  обоих  множеств    и    отсортированы  по  возрастанию  значений  и  полагаем    и  .

Даны    и  и  пороговая  величина  решения  ,  пусть    будет  множеством  всех  выполнимых  (допустимых)  упаковок  данных  элементов  в  лист  размера  ,  который  может  произвести  (вместе  с  остаточными  элементами  и  листом)  прибыль,  больше,  или  равное  .  Для  двух  данных  выполнимых  упаковок    и    мы  формально  обозначаем  через    попарную  сумму  упаковок  в  множества    и  :

Интуитивно,    является  множеством  упаковок,  которые  могут  быть  получены,  комбинацией  любой  упаковки    с  любой  упаковкой  ,  независимо  от  размеров  множеств    и  .  Ясно,  что  как  только  множество    определено  мы  можем  найти  множества    с  условием,  что  все    (соответственно  ),  элементы  принадлежат  упорядоченному  множеству    (соответственно  ).  Похожим  способом  знание  множества    позволяет  нам  определять  множества  .  Действительно,  достаточно  отметить,  что  каждая  упаковка  ,  которая  может  произвести  прибыль,  по  крайней  мере  равную  ,  в  прямоугольнике  ,  может  быть  получена  как  сумма  двух  допустимых  упаковок  определенных  для  прямоугольника  меньших  размеров.  Формально:  ,  где  либо    и    для  некоторого  ,  либо    и    для  некоторого  .  Таким  образом,  зная    и    для  каждого    и  ,  мы  можем  легко  получить  (сгенерировать)  рекурсивным  способом  . 

Основной  алгоритм  может  быть  улучшен  следующим  образом.  Для  каждой  упаковки  на  листе  ширины    и  высоты  ,  верхняя  граница,  скажем  ,  максимальной  прибыли,  может  быть  получена,  когда  остаточная  площадь  вычислена.  С  этой  целью  рассмотрим  примеры  рюкзаков  с  вместимостью  ,    типов  элементов,    возможных  в    копий,  каждый  с  прибылью  и  весом  .  Оптимальное  решение  из  этого  случая  или  любая  верхняя  граница  этой  величины  дает  верхнюю  границу  для  максимальной  прибыли,  которая  может  быть  получена,  упаковывая  остающиеся  элементы  в  остаточную  часть  листа.  Ясно,  что  все  элементы  ,  такие,  что    могут  быть  удалены  из  множества  ,  так  как  они  не  могут  привести  к  выполнимому  решению,  имеющему  прибыль  больше,  чем  .  В  нашей  реализации  мы  вычисляем  величину  верхней  границы    на  оптимальном  решении  (одномерного)  случая  задачи  рюкзака  (см.  [5]).  Величины  верхних  границ    и    полученные  Хайфи  [4]  и  эти  же  величины,  предложенные  Янг-Гуном  и  Кангом  [7]  для  двумерной  (ортогональной)  задачи  рюкзака  без  ограничений,  мы  используем  минимум  этих  величин  как  верхнюю  границу.

Кроме  того,  отметим,  что  ширина  и  высота  листа  могут  быть  уменьшены  до    и  ,  соответственно,  что  приводит  к  меньшей  мощности  рюкзака,  при  решении  релаксации  задачи  рюкзака,  следовательно,  к  более  точным  верхним  границам.  Наконец,  отметим,  что  только  максимальная  допустимая  упаковка  должна  быть  сохранена  для  каждого  набора  ,  и  что  любой  не  максимальный  элемент  может  быть  игнорирован.  Это  сокращает  количество  элементы  в  ,  следовательно,  требования  к  памяти  и  времени  вычисления  алгоритма.

8.  Входные  и  выходные  данные  системы

Входные  данные:

1.  Ширина  прямоугольника-листа;

2.  Высота  прямоугольника-листа;

3.  Размеры  квадратов;

Выходные  данные:

5.  Прямоугольники,  расположенные  на  экране  монитора;

6.  Текстовый  файл  с  информацией  о  вписанных  прямоугольниках;

7.  Дополнительная  информация  о  вписывании  прямоугольников  в  виде  различных  сообщений  на  экране.

8.5.             Разработка  интерфейса  пользователя

Интерфейс  пользователя  целесообразно  делать  в  графическом  виде,  так  как  это  максимально  удобно  для  использования.

Форма  ввода  и  вывода  данных

Рисунок  1.  Интерфейс  пользователя

Вводим  сначала  ширину  прямоугольника,  нажимаем  enter,  высоту  —  enter,  и  вводим  размеры  квадратов,  например  23  —  enter,  45  —  enter  и  т.  д.,  нажимаем  0,  для  прекращения  ввода  квадратов  и  в  том  месте,  где  сохранен  проект,  появляется  файл  result.png,  где  можно  увидеть  упаковку  квадратов. 

В  этом  же  окне  выводится  информация  о  количестве  квадратов  определенных  размеров.  Нажимаем  0  и  видим  информацию  о  времени  заполнения  прямоугольной  область  квадратами. 

После  всех  проделанных  действий  получаем:

Рисунок  2.  Полученный  результат  программы

и  саму  упаковку:

Рисунок  3.  Упаковка  квадратов  в  прямоугольник

Таблица  1.

Численные  результаты  программы

Вывод:  чем  больше  введенных  квадратов,  тем  больше  время  выполнения  алгоритма.

9.  Заключение

В  соответствии  с  целью  исследования  были  поставлены  и  выполнены  следующие  задачи:

1.  Формулировка  рассматриваемых  задач  раскроя-упаковки  в  терминах  математического  программирования  и  качественная  оценка  методов  их  решения;

2.  Разработан  и  исследован  алгоритм  решения  задачи  упаковки  квадратов  различных  размеров  в  прямоугольник;

3.  Проведен  анализ  эффективности  разработанного  метода  на  основе  результатов  численных  экспериментов. 

Список  литературы:

1.Техтран/Раскрой  листового  материала  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://9132222.ru/catalog/soft/techtran/textran.html  (дата  обращения  12.06.2014).

2.Caprara  A,  Monaci  M.  On  the  two-dimensional  knapsack  problem.  Operations  Research  Letters  2004;32:5–14. 

3.Christofides  N,  Whitlock  C.  An  algorithm  for  two-dimensional  cutting  problems.  Operations  Research  1977;25:30–44. 

4.Hifi  M.  An  improvement  of  Viswanathan  and  Bagchi’s  exact  algorithm  for  constrained  two-dimensional  cutting  stock.  Computers  and  Operations  Research  1997;24:727–36. 

5.Martello  S,  Toth  P.  Knapsack  problems:  algorithms  and  computer  implementations.  Chichester:  John  Wiley  &  Sons;  1990. 

6.Pisinger  D,  Sigurd  M.  Using  decomposition  techniques  and  constraint  programming  for  solving  the  two-dimensional  bin-packing  problem.  INFORMS  Journal  on  Computing  2007;19:36–51

7.Young-Gun  G,  Kang  MK.  A  new  upper  bound  for  unconstrained  two-dimen-sional  cutting  and  packing.  Journal  of  the  Operational  Research  Society  2002;53:587–91.