ЭЛЕМЕНТЫ  ЛИНЕЙНОЙ  АЛГЕБРЫ  В  ЗАДАЧАХ  ЭКОНОМИЧЕСКОГО  СОДЕРЖАНИЯ

Чуркина  Людмила  Александровна

студент  2  курса,  предметно-цикловая  комиссия  физико-математических  дисциплин  КЭиБ  ОГУ,  РФ,  г.  Оренбург

E -mail:  Salbert230@Gmail.com

Нурманова  Сабиля  Андреевна

научный  руководитель,  преподаватель  КЭиБ  ОГУ,  РФ,  г.  Оренбург

Математика  и  экономика-это  самостоятельные  области  знаний,  которые  имеют  свой  объект  и  предмет  исследования.  Понятие  матрицы  и  основанный  на  нем  раздел  математики,  который  называется,  матричная  алгебра,  имеют  большое  значение  для  экономистов,  основная  часть  математических  моделей  экономических  объектов  и  процессов  записывается  в  простой  и  компактной  матричной  форме. 

Матричной  алгеброй  называют  область  математики,  которая  изучает  алгебраические  операции  над  числовыми  массивами,  записанными  в  форме  строк  и  столбцов.  Матричная  алгебра  относится  к  числу  наиболее  важных  для  экономистов  областей  математики.  Объясняется  это  тем,  что  записываются  в  матричной  форме:  математические  модели  отражающие  взаимосвязи  экономических  структур,  динамику  их  развития,  многообразие  действующих  факторов.  Это  в  свою  очередь  позволяет  использовать  современные  методы  матричной  алгебры  в  экономических  исследованиях  и  расчетах.  Чтобы  интерпретировать  математически  закономерности  реальных  явлений  в  экономике,  используют  математические  модели  относительно  одной  или  нескольких  переменных.  Ни  одна  модель  не  может  полностью  отражать  все  многообразие  действительного  мира  и  является  лишь  некоторым  его  приближением.  Широкое  распространение  в  экономических  исследованиях  получили  линейные  модели,  которые  нередко  с  высокой  точностью  соответствуют  описываемым  ими  явлениям.  Многие  линейные  модели  сводятся  к  системам  алгебраических  линейных  уравнений  или  неравенств.

Между  экономикой  и  математикой  существует  как  прямая,  так  и  обратная  связь:  создание  нового  математического  аппарата  и  его  применение  позволяет  экономике  по-новому  решать  существующие  задачи.

Экономика  ставит  перед  математикой  новые  задачи  и  стимулирует  поиск  методов  их  решения.

Применение  математики  в  экономических  исследованиях,  позволяет  объяснить  прошлое,  увидеть  будущее  и  оценить  последствия  действий,  которые  потребует  еще  огромных  усилий,  новых  фундаментальных  знаний.  С  помощью  матриц  удобно  описывать  различные  экономические  закономерности.  Например,  различные  таблицы,  которые  содержат  в  себе  разные  данные,  какого-либо  предприятия.  Рассмотри  на  примере  задач  экономического  содержания.

Задача  №  1.

Побывав  на  Оренбургском  Локомотиворемонтном  Заводе,  были  определены  ежесуточные  экономические  показатели  ОЛРЗ,  которые  представлены  в  таблице  1.

Таблица  1.

Экономические  показатели  ОЛРЗ

Найти:  цены,  расходы  и  затраты  сырья.

Решение:

Введем  четыре  вектора  для  рассмотрения  производственного  процесса.

  —  вектор  цены.

  —  вектор  времени  .

  —  вектор  расхода  сырья.

  —  вектор  изделия  товара.

В  соответствие  с  данными  таблицами  получим:

  =  (  30000,  58,  2500,  200)

=  (72,  15,  42,20)

=  (  8,  1,  2,  9)

=  (5,  500,  2,  5)

Заметим,  что  соответствующие  скалярные  произведения  векторов,  будут  представлять  собой  искомые  величины,  которые  делиться  на  три  других  вектора.

*=8*5+1*500+2*2+9*5=40+500+4+45=589  килограмм

*=5*72+500*15+2*42+5*20=360+7500+84+100=8  044  часа

*=30000*5+58*500+2500*2+200*5=150000+29000+500+1000=180  500  денежных  единиц.

Ответ:   589  килограмм,  8044  часа  и  180  500  денежных  единиц.

Задача  №  2.

В  этой  задаче  работникам  ОЛРЗ,  по  трем  категориям  выплатили  заработную  плату  наличными,  с  такими  купюрами  как  100  рублей  —  30  купюр,  500  рублей  —  70  купюр,  1000  рублей  —  50  купюр.  Причем,  I  категории  выдали  1000  рублей,  II  категории  —  2000,  III  категории  —  3000.  Нужно  определить,  сколько  сотрудников  каждой  категории  работает  на  предприятие,  если  каждому  работнику  заработную  плату  выдали  минимальным  числом  купюр. 

Для  начала  составим  таблицу,  где  x1,x2,x3-количество  работников  с  I  по  III  категорию.

Таблица  2. 

Экономические  показатели  заработной  платны  ОЛРЗ

Теперь  составлю  систему  линейных  уравнений  решим  систему  методом  Гаусса.

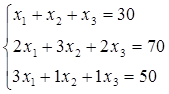
Находим  D  по  правилу  треугольника  Сарруса

D 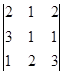 ==6+12+1-2-9-4=4,4=0,  делаем  вывод  что  решение  существует.

Затем,  составляю  расширенную  матрицу  системы,  приписывая  справой  стороны  главной  матрицы  системы  матрицы  свободных  членов  (A/B)

(A/B)= 

С  помощью  элементарных  преобразований  приводим  расширенную  матрицу  к  треугольному  виду.  Прямой  ход.

Для  этого  прибавляю  (-2)  ко  второй  строке  и  (-3)  к  третьей  строке.  Получим:

(A/B)=  =

Теперь  умножим  третью  строку  матрицы  на  (-1/2)  и  прибавляю  (-1)

(A/B)=  ====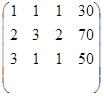

==

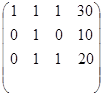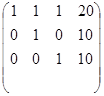Выполняем  обратный  ход,  то  есть  из  матрицы  треугольного  вида  последовательно  находят  неизвестные.

В  нашем  случае,  X₁,  X₂,  X₃  равны  10.

Ответ:   10  сотрудников  каждой  категории  работает  на  предприятие,  если  каждому  работнику  заработную  плату  выдать  минимальным  числом  купюр. 

Задача  №  3.

Побывав  на  трех  предприятиях,  занимающиеся  выпуском  различной  продукции.  Каждое  предприятие  выпускает  3  вида  продукции  с  потреблением  трех  разных  видов  сырья,  у  каждого  есть  продолжительность  работы  в  году,  а  так  же  цена. 

Определить:

1.  Производительность  каждого  предприятия,  по  каждому  виду  изделия  за  год.

2.  Потребность  каждого  предприятия  по  каждому  виду  сырья  за  год.

3.  Родовую  сумму  каждого  предприятия  для  закупки  сырья,  необходимого  при  определенном  количестве  рабочих  дней  и  выпуска  изделий.

Начнем  с  того  что  составим  таблицу  со  всеми  нашими  данными.

Таблица  3.

Экономические  показания  трех  предприятий

Теперь  составим  матрицы,  которые  представляют  экономическую  совокупность  производства.

B=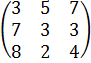 

Построив  нашу  таблицу  мы  знаем,  что  каждый  столбец  матрицы  соответствует  производительности  каждого  предприятия  по  каждому  виду  продукции.  Отсюда  следует,  что  годовая  производительность  каждого  предприятия  по  каждому  виду  продукции  получается  умножение  первого  столбца  матрицы  A  на  количество  рабочих  дней  в  году,  для  каждого  предприятия  (i=1,2,3,4,5),  где  i-это  количество  рабочих  дней  в  году.  Таким  образом  годовая  производительность  каждого  предприятия  по  каждому  изделию  описывается  матрицей.

B_ГОД.=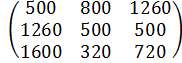

Матрица  затрат  сырья  на  единицу  изделия  имеет  вид:

C=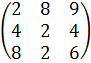 

Теперь,  для  того  чтобы  определить  расход  по  всем  видам  сырья,  необходимо  матрицу  B  умножить  на  матрицу  C.

B*C=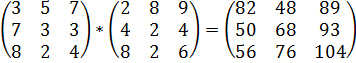 

Чтобы  получить  ответ  на  второй  вопрос  моей  задачи,  мы  должны  матрицу  BC  умножить  на  количество  дней,  обработанных  за  год.

Каждую  строку  матрицы  B  умножаю  на  столбец  матрицы  C

*===

=

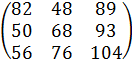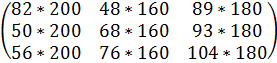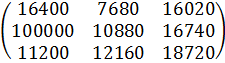
Чтобы  определить  стоимость  годового  запаса  сырья  для  каждого  предприятия  необходимо  матрицу  СB_год  умножить  на  вектор  d,  где  вектор  d  это  стоимость  сырья,  то  есть  d=(200,100,50)

=

=

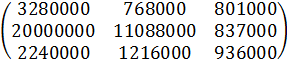
Следовательно,  мы  нашли  суммы  кредитования  предприятий  для  закупки  сырья,  которые  определяются  соответствующим  компонентам  вектора  d.

Ответ: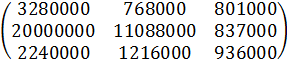 

Вывод:  Рассмотрев  теоретические  аспекты  линейной  алгебры,  мы  применили  изученный  нами  материал  к  решению  задач  экономического  содержания  на  примере  ОЛРЗ,  что  позволило  сформировать  навыки  умения  решений  экономических  задач.

Список  литературы:

1.Красс  М.С.,  Чупрынов  Б.П.  Математика  для  экономистов:  учеб.  пособие.  Спб.:  Питер,  2005.  —  466  с.

2.Кремер  Н.Ш.  Высшая  математика  для  экономистов:  учебник.  М.:  ЮНИТИ-ДАНА,  2010  —  479  с. 

3.Сирл  С.,  Госман  У.  Матричная  алгебра  в  экономике  /  Пер.  с  англ.  и  научное  редактирование  Е.М.  Четыркина  и  Р.М.  Энтова.  М.:  Статистика  1974  —  375  с.