Статья опубликована в рамках: XVI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 21 января 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
О ПРИБЛИЖЕННЫХ ФОРМУЛАХ ДЛЯ ИНТЕГРАЛОВ ТИПА ИНТЕГРАЛА ПУАССОНА
Олькин Михаил Артурович
студент 3 курса, инженерный факультет, филиал СКФУ в г. Пятигорске, РФ, г. Пятигорск
;
Тимченко Ольга Викторовна
научный руководитель, канд. экон. наук, кафедра физико-математических дисциплин, филиал СКФУ в г. Пятигорске, РФ, г. Пятигорск
Хорошо известно, что интеграл Эйлера-Пуассона 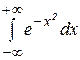 не выражается через элементарные функции («неберущийся» интеграл) и, соответственно, нет аналитических выражений для таких часто встречающихся в приложениях специальных функций как
не выражается через элементарные функции («неберущийся» интеграл) и, соответственно, нет аналитических выражений для таких часто встречающихся в приложениях специальных функций как
 — функция ошибок,
— функция ошибок,
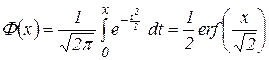 — интеграл вероятности,
— интеграл вероятности,
 — нормальная функция распределения.
— нормальная функция распределения.
В приложениях приходится довольствоваться результатом табулирования.
Не только интерес, но и практическую ценность представляют, по нашему мнению, приближенные аналитические выражения для этих функций, если они с одной стороны достаточно просты, а с другой достаточно точны 0,1 %—1 %. Именно эта задача решается в данной работе.
Хорошо известна также схема [1, с. 661], позволяющая вычислить несобственный интеграл  . (*)
. (*)
Именно этой схемой мы намерены воспользоваться для оценки интеграла
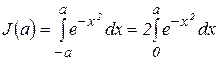 (1)
(1)
Сводим вычисление интеграла (1) к вычислению двойного интеграла. Имеем
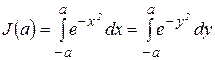 ,
,
тогда
 (2)
(2)
Здесь область интегрирования ![]() — квадрат со стороной
— квадрат со стороной ![]() ,
, ![]() (рисунок 1):
(рисунок 1):

Рисунок 1. Область интегрирования
Область интегрирования ![]() разбиваем на две:
разбиваем на две:
![]() — круг радиуса
— круг радиуса ![]() , по которому вычисляется точное («нулевое приближение») для интеграла (2), и
, по которому вычисляется точное («нулевое приближение») для интеграла (2), и
область ![]() — четыре криволинейные треугольные области вида
— четыре криволинейные треугольные области вида ![]() , или, восемь треугольных областей вида
, или, восемь треугольных областей вида ![]() .
.
Геометрически добавка к нулевому приближению — это объем восьми одинаковых цилиндрических тел, в основании которых криволинейный треугольник ![]() (
(![]() — дуга окружности радиуса
— дуга окружности радиуса ![]() ) и «шапка» — поверхность
) и «шапка» — поверхность ![]() . «Неберущаяся» часть интеграла (2) связана как раз с вычислением объема по области
. «Неберущаяся» часть интеграла (2) связана как раз с вычислением объема по области ![]() . Имеем
. Имеем
 (3)
(3)
По области ![]() интеграл вычисляется переходом к полярным координатам
интеграл вычисляется переходом к полярным координатам ![]() . Имеем
. Имеем
 (4)
(4)
Соответственно, «нулевое» приближение для интеграла (1) дается выражением:
![]() (5)
(5)
При ![]()
![]() , а при
, а при ![]()
![]() . В этом приближении для интеграла ошибок и интеграла вероятностей получаем (с недостатком)
. В этом приближении для интеграла ошибок и интеграла вероятностей получаем (с недостатком)
![]() ,
,
![]() (6)
(6)
Значения этих выражений на 9 %—11 % меньше табличных для практических все ![]() значимой области, что неприемлемо много для большей части приложений.
значимой области, что неприемлемо много для большей части приложений.
Если при выборе нулевого приближения (1) область ![]() взять в виде круга радиуса
взять в виде круга радиуса ![]() (приближение с избытком), то для этих функций получаем выражения
(приближение с избытком), то для этих функций получаем выражения
![]() ,
,
![]() ,
,
![]() ,
,
значения которых на 20 %—25 % больше табличных. В качестве нулевого приближения выбираем (5), (6).
Для улучшения результата надо вычислить добавку к ![]() , равную
, равную ![]() .
.
 (7)
(7)
или
![]() .
.
Переходя к полярным координатам, получаем
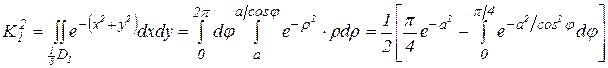 (8)
(8)
«Неберущаяся» часть исходного интеграла связана с функцией 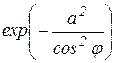 интеграла (8). Для его оценки заметим, что
интеграла (8). Для его оценки заметим, что  для
для  монотонно растет от 1 до 2, а среднее значение промежуточного аргумента
монотонно растет от 1 до 2, а среднее значение промежуточного аргумента 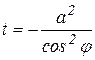 экспоненты на этом интервале будет
экспоненты на этом интервале будет
 .
.
Раскладывая ![]() возле точки
возле точки ![]() в ряд по степеням
в ряд по степеням ![]() получим для «неберущейся» части интеграла выражение
получим для «неберущейся» части интеграла выражение
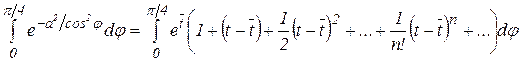 .
.
Учитывая, что
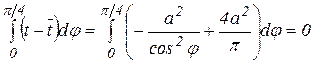 и,
и,
оставляя в разложении только нулевой член ![]() , находим оценку
, находим оценку ![]() в этом приближении:
в этом приближении:
![]() .
.
Учитывая, что
![]() , получаем для
, получаем для ![]()
![]() (9)
(9)
А для искомого интеграла (1) выражение
![]() (10)
(10)
Соответственно, для интеграла ошибок и интеграла вероятностей искомые приближенные выражения имеют вид
![]() (11)
(11)
![]() (12)
(12)
Значения ![]() и
и ![]() вычисляемые по этим формулам для
вычисляемые по этим формулам для ![]() отличаются от табличных на сотые доли процентов и меньше, а для
отличаются от табличных на сотые доли процентов и меньше, а для ![]() — на десятые доли, что для приложений означает практическую достоверность результата вычислений (таблица 1) [2, c. 470]. Учет при интегрировании квадратичного члена
— на десятые доли, что для приложений означает практическую достоверность результата вычислений (таблица 1) [2, c. 470]. Учет при интегрировании квадратичного члена ![]() в этих условиях представляется ненужным усложнением формул (10)—(12).
в этих условиях представляется ненужным усложнением формул (10)—(12).
Таблица 1.
Значения функций табличные и вычисленные приближенно

Список литературы:
1.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: в 3 т. Т. 2. М.: ФИЗМАТЛИТ, 2001. — 864 с.
2.Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2003. — 479 с.
дипломов


Оставить комментарий