Статья опубликована в рамках: XV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 24 декабря 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ЗАДАЧИ C2 ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ НА НАХОЖДЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПЛОСКОСТИ
Куликова Анастасия Юрьевна
студент 5 курса, кафедра мат. анализа, алгебры и геометрии ЕИ КФУ, РФ, Республика Татарстан, г. Елабуга
Ганеева Айгуль Рифовна
научный руководитель, канд. пед. наук, доцент ЕИ КФУ, РФ, Республика Татарстан, г. Елабуга
В заданиях ЕГЭ по математике в последние годы появляются задачи на вычисление расстояния от точки до плоскости. В данной статье на примере одной задачи рассмотрены различные методы нахождения расстояния от точки до плоскости. Для решения различных задач можно использовать наиболее подходящий метод. Решив задачу одним методом, другим методом можно проверить правильность полученного результата.
Определение. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на данную плоскость.
Задача. Дан прямоугольный параллелепипед АBСDA1B1C1D1 со сторонами AB=2, BC=4, AA1=6. Найдите расстояние от точки D до плоскости АСD1.
1 способ. Используя определение. Найти расстояние r(D, АСD1) от точки D до плоскости АСD1 (рис. 1).
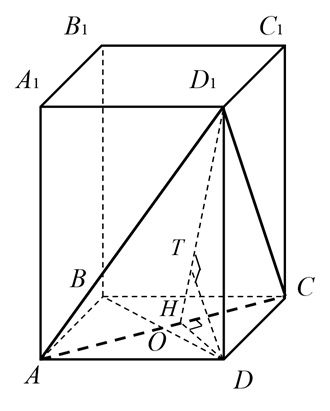
Рисунок 1. Первый способ
Проведем DH⊥АС, следовательно по тереме о трех перпендикулярах D1H⊥АС и (DD1H)⊥АС. Проведем прямую DT перпендикулярно D1H. Прямая DT лежит в плоскости DD1H, следовательно DT⊥AC. Следовательно, DT⊥АСD1.
Из прямоугольного треугольника АDC найдем гипотенузу АС и высоту DH
![]()
![]()
Из прямоугольного треугольника D1DH найдем гипотенузу D1H и высоту DT
![]()
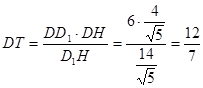
Ответ: ![]() .
.
2 способ. Метод объемов (использование вспомогательной пирамиды). Задачу данного типа можно свести к задаче о вычислении высоты пирамиды, где высота пирамиды является искомым расстоянием от точки до плоскости. Доказать, что эта высота и есть искомое расстояние; найти объём этой пирамиды двумя способами и выразить эту высоту.
Отметим, что при данном методе нет необходимости в построении перпендикуляра из данной точки к данной плоскости.
Прямоугольный параллелепипед — параллелепипед, все грани которого являются прямоугольниками.
AB=CD=2, BC=AD=4, AA1=6.
Искомым расстоянием будет высота h пирамиды ACD1D, опущенной из вершины D на основание ACD1 (рис. 2).
Вычислим объем пирамиды ACD1D двумя способами.
Вычисляя, первым способом за основание примем ∆ ACD1, тогда
![]()
Вычисляя, вторым способом за основание примем ∆ ACD, тогда
![]()
Приравняем правые части последних двух равенств, получим
![]()
![]()
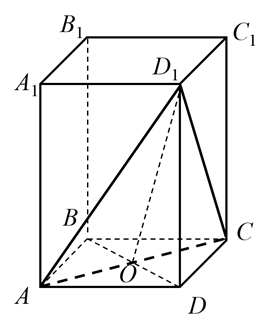
Рисунок 2. Второй способ
Из прямоугольных треугольников АСD, ADD1, CDD1 найдем гипотенузы, используя теорему Пифагора
![]()
![]()
![]()
![]()
Вычислим площадь треугольника ACD
![]()
Вычислим площадь треугольника АСD1, используя формулу Герона
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]() .
.
3 способ. Координатный метод.
Пусть дана точка M(x0,y0,z0) и плоскость α, заданная уравнением ax+by+cz+d=0 в прямоугольной декартовой системе координат. Расстояние от точки M до плоскости α можно вычислить по формуле:

Введем систему координат (рис. 3). Начало координат в точке В;
прямая АВ — ось х, прямая ВС — ось y, прямая BB1 — ось z.
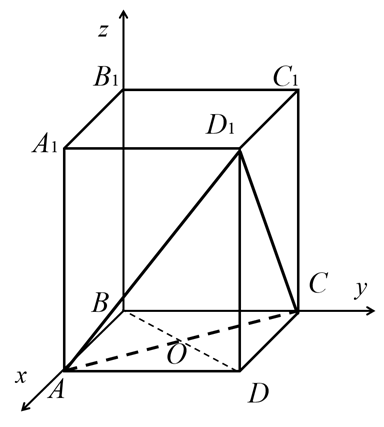
Рисунок 3. Третий способ
B(0,0,0), А(2,0,0), С(0,4,0), D(2,4,0), D1(2,4,6).
Пусть aх+by+cz+d=0 – уравнение плоскости ACD1. Подставляя в него координаты точек A, C, D1 получим:
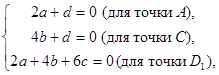
![]()
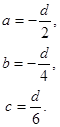
![]()
Уравнение плоскости ACD1 примет вид
![]()
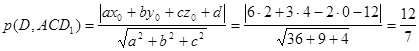
Ответ: ![]() .
.
4 способ. Векторный метод.
Введем базис (рис. 4) ![]()
![]() ,
, ![]() .
.
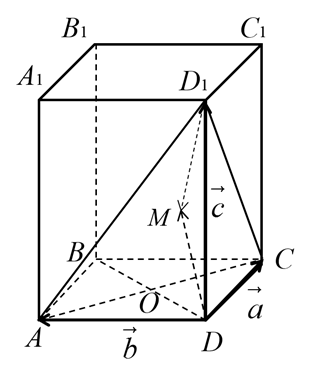
Рисунок 4. Четвертый способ
![]()
![]()
![]()
![]()
Поэтому ![]()
![]()
Далее имеем:
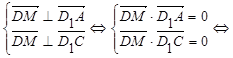

Так как ![]()
![]()
![]()
![]()
![]()
то имеем: 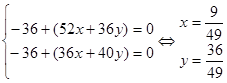
Отсюда получаем:
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]()
Список литературы:
1.Корняков А.Н. Материалы курса «Готовим к ЕГЭ хорошистов и отличников»: лекции 5—8 \ А.Н. Корняков, А.А. Прокофьев. М.: Педагогический университет «Первое сентября», 2012. — 100 с.
отправлен участнику


Оставить комментарий