ВЛИЯНИЕ  ДОПОЛНИТЕЛЬНЫХ  СВЯЗЕЙ  НА  УСТОЙЧИВОСТЬ  НЕЙРОННЫХ  СЕТЕЙ  КУБИЧЕСКОЙ  И  КОЛЬЦЕВОЙ  КОНФИГУРАЦИИ

Аюпова  Юлия  Рафаэлевна,

Стаканов  Станислав  Александрович

c туденты  4  курса,  кафедра  математического  анализа  ЮУрГУ,  РФ,  г.  Челябинск

Кипнис  Михаил  Маркович

научный  руководитель,  д-р  физ.-мат.  наук,  профессор  ЧГПУ,  РФ,  г.  Челябинск

Работа  поддержана  грантом  Минобразования  России  в  рамках  государственного  задания  Челябинскому  государственному  педагогическому  университету  на  2014  год.

Исследована  устойчивость  нейронных  сетей  кубической  и  кольцевой  конфигураций  с  различным  количеством  нейронов.  Задача  сводится  к  проблеме  устойчивости  матричных  разностных  уравнений  с  запаздыванием.

1.  Введение

Мы  рассматриваем  пары  нейронных  сетей,  в  которых  первая  сеть  представляет  собой  кольцевую  или  кубическую,  вторая  её  же,  но  с  перемычкой.

Приведём  типы  рассмотренных  нейронных  сетей:

1.  Кольцевая  нейронная  сеть  с  четырьмя  нейронами  (Рисунок  1).

2.  Кольцевая  нейронная  сеть  с  шестью  нейронами  (Рисунок  2).

3.  Нейронная  сеть,  в  виде  двумерного  куба  (Рисунок  3).

4.  Нейронная  сеть,  в  виде  трехмерного  куба  (Рисунок  4).

Рисунок  1а.  Кольцевая  структура  с  четырьмя  нейронами

Рисунок  1б.  Кольцевая  структура  с  четырьмя  нейронами  и  перемычкой

Рисунок  2а.  Структура  двумерного  куба  с  четырьмя  нейронами

Рисунок  2б.  Структура  двумерного  куба  с  четырьмя  нейронами  и  перемычкой

Рисунок  3а.  Кольцевая  структура  с  шестью  нейронами

Рисунок  3б.  Кольцевая  структура  с  шестью  нейронами  и  перемычкой

Рисунок  4а.  Структура  трехмерного  куба  с  восьмью  нейронами

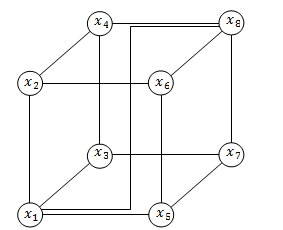
Рисунок  4б.  Структура  трехмерного  куба  с  восьмью  нейронами  и  перемычкой

Искусственные  нейронные  сети  с    нейронами  в  дискретном  линеаризованном  варианте  описываются  разностными  уравнениями

          …                         (1)

Здесь    матрицы  размера  ,  натуральное  число    есть  номер  такта,    является    мерным  вектором  состояний  нейронной  сети  в  момент  .  есть  матрица  мгновенных  взаимодействий  нейронов,    —  матрица  взаимодействий  с  запаздыванием.

Матрица  для  кольцевой  сети  с  четырьмя  нейронами  имеет  вид:

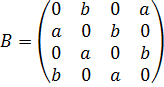
Матрица  для  кольцевой  сети  с  четырьмя  нейронами  и  перемычкой  имеет  вид:

Матрица  для  кольцевой  сети  с  шестью  нейронами  имеет  вид:

Матрица  для  кольцевой  сети  с  шестью  нейронами  и  перемычкой  имеет  вид:

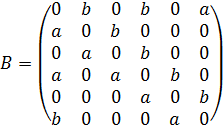
Матрица  для  кубической  сети  с  четырьмя  нейронами  имеет  вид:

Матрица  для  кубической  сети  с  четырьмя  нейронами  и  перемычкой  имеет  вид:

Матрица  для  кубической  сети  с  четырьмя  нейронами  и  перемычкой  имеет  вид:

Матрица  для  кубической  сети  с  четырьмя  нейронами  и  перемычкой  имеет  вид:

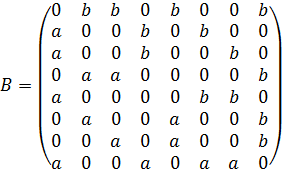
Для  разностного  матричного  уравнения  (1)  характеристическим  уравнением  является  уравнение 

Если  все  корни    уравнения  (4)  обладают  свойством  ,  то  уравнение  (1)  является  устойчивым,  то  есть  все  его  решения  стремятся  к  нулю  при.  Если  хотя  бы  для  одного    выполняется  неравенство  ,  то  уравнение  (1)  неустойчиво.

Для  изучения  устойчивости  уравнения  (1)  мы  использовали  программу  MathCAD.  Мы  фиксируем  запаздывание    и  число  нейронов  ,  а  также  коэффициент  демпфирования  .  Затем  перебираем  значения    из  некоторого  интервала  с  некоторым  шагом.  Для  каждого  значения    мы  посредством  вычисления  корней  характеристического  уравнения  подбираем  граничные  значения  ,  в  окрестности  которых  устойчивость  системы  граничит  с  неустойчивостью.  В  результате  мы  получаем  область  устойчивости  в  пространстве  параметров 

2.  Результаты  численных  экспериментов  по  определению  областей  устойчивости 

Мы  получили  следующие  результаты  численных  экспериментов.

На  всех  графиках  синим  обозначена  область  устойчивости  сети  без  перемычки,  красным  сети  с  перемычкой.

Рисунок  5.  Области  устойчивости  в  плоскости    для  кольцевой  нейронной  (4  нейронов)  сети  с  перемычкой  и  без  нее  при  запаздывании    и  коэффициенте  демпфирования  .

Рисунок  6.  Области  устойчивости  в  плоскости    для  кольцевой  нейронной  (6  нейронов)  сети  с  перемычкой  и  без  нее  при  запаздывании    и  коэффициенте  демпфирования  .

Рисунок  7.  Области  устойчивости  в  плоскости    для  кубической  нейронной  (4  нейрона)  сети  с  перемычкой  и  без  нее  при  запаздывании  и  коэффициенте  демпфирования 

Рисунок  8.  Области  устойчивости  в  плоскости    для  кубической  нейронной  (8  нейронов)  сети  с  перемычкой  и  без  нее  при  запаздывании    и  коэффициенте  демпфирования  .

Заключение

Появление  перемычки  в  нейронной  сети  делает  ее  так  называемой  сетью  smallworld.  Последний  термин  связан  с  гипотезой  о  шести  рукопожатиях  [2].  Из  общих  соображений  ясно,  что  появление  перемычки  должно  уменьшать  область  устойчивости  нейронной  сети.  Наши  численные  эксперименты  в  основном  подтверждают  эту  гипотезу.  Однако  существуют  некоторые  незначительные  области  в  плоскости  ,  в  которых  эта  гипотеза  не  подтверждается.  Такие  области  по  аналогии  с  работой  [4]  естественно  назвать  парадоксальными.

Данная  работа  продолжает  исследования  устойчивости  нейронных  сетей  [1,  3,  4].

Список  литературы:

1.Речкалова  Л.В.,  Кипнис  М.М.,  Область  устойчивости  нейронной  сети  с  топологией  тора  при  разрыве  некоторых  связей,  Сб.  статей  по  материалам  XXXVIII  Международной  научно-практической  конференции  «Инновации  в  науке»,  Новосибирск,  27  дек.  2013,  —  с.  23—30. 

2.Теория  шести  рукопожатий  //Википедия:  свободная  энциклопедия.  2011.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ru.wikipedia.org/wiki/Теория_шести_рукопожатий/  (дата  обращения:  20.03.2014).

3.Khokhlova  T.N.,  Kipnis  M.M.  Numerical  and  qualitative  stability  analysis  of  ring  and  linear  neural  networks  with  a  large  number  of  neurons.  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  76(3),  —  pp.  403—419.

4.Khokhlova  T.N.,  Kipnis  M.M.,  The  breaking  of  a  delayed  ring  neural  network  contributes  to  stability:  The  rule  and  exceptions,  Neural  Networks,  —  2013,  —  V.  48,  —  p.    148—152.