"За статью проголосовало 2 человека"

МЕТОД  МОНТЕ-КАРЛО  ДЛЯ  РЕШЕНИЯ  ЗАДАЧИ  КОММИВОЯЖЁРА

Зенг  Валерия  Андреевна

студент  3  курса,  кафедра  «Дизайн  и  технологии  медиаиндустрии»  ОмГТУ,  РФ,  г.  Омск

E-mail:  valeriyazeng@mail.ru

Нифонтова  Людмила  Сергеевна

студент  3  курса,  кафедра  теплоэнергетики  ОмГТУ,  РФ,  г.  Омск

E-mail: 

Степанов  Владимир  Николаевич

научный  руководитель,  канд.  физ.-мат.наук,  доцент  каф.«Высшая  математика»  ОмГТУ,  РФ,  г.  Омск

Задача  коммивояжёра  является  классической  задачей  дискретной  оптимизации  и  имеет  многочисленные  приложения:  транспортные  задачи,  задачи  соединения  пунктов  линией  электропередач  и  т.  д.  Задача  коммивояжера  состоит  в  следующем:  он  должен  объехать  ряд  населенных  пунктов,  пробыв  в  каждом  пункте  только  один  раз  и  вернуться  в  исходный  пункт.  Какой  маршрут  должен  выбрать  коммивояжёр,  чтобы  пройденный  путь  был  наименьшей  длины?  [1,  с.  59].

Решение  задачи  коммивояжера  методом  Монте-Карло  строится  на  случайном  выборе  каждого  следующего  города,  через  который  будет  проходить  путь.  При  использовании  программы  ответ  носит  вероятностный  характер  и  может  сильно  отличаться  от  правильного  решения  задачи  коммивояжера.  Но  при  увеличении  числа  испытаний  погрешность  ответа  уменьшается  [2,  с.  395].

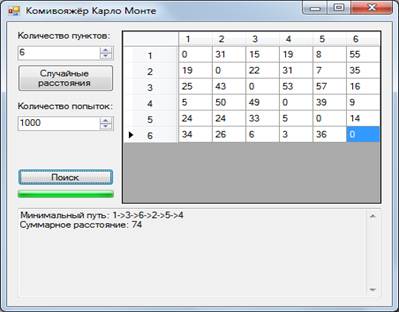
Рисунок  1  Внешний  вид  программы

Пусть  имеется  полный  граф  с  n  вершинами,  заданный  матрицей  расстояний  С  =  ||с_ij||.  Вершину  v₁  примем  за  начальную  и  случайным  образом  выберем  остальные  вершины  [1,  с.  80].  В  программе  это  выглядит  так: 

public  partial  class  Form1  :  Form

{

  int  N;

  public  Form1()

  {

  InitializeComponent();

  }

private  void  numericUpDown1_ValueChanged(object  sender,  EventArgs  e)

  {

  N  =  (int)numericUpDown1.Value;

  dataGridView1.RowCount  =  N;

  dataGridView1.ColumnCount  =  N;

  for  (int  i  =  0;  i  <  N;  i++)

  {

  dataGridView1.Rows[i].HeaderCell.Value  =  ""  +  (i  +  1);

  dataGridView1.Columns[i].HeaderText  =  ""  +  (i  +  1);

  }

  }

private  void  button1_Click(object  sender,  EventArgs  e)

{

  Random  r  =  new  Random();

  for  (int  i  =  0;  i  <  N;  i++)

  for  (int  j  =  0;  j  <  N;  j++)

  dataGridView1[i,  j].Value  =  r.Next(0,  10);

  }

private  void  button2_Click(object  sender,  EventArgs  e)

  {

  double[,]  A  =  new  double[N,  N];

  for  (int  i  =  0;  i  <  N;  i++)

  for  (int  j  =  0;  j  <  N;  j++)

  A[i,j]  =  Convert.ToDouble(dataGridView1[j,  i].Value);

  textBox1.Text  =  "";

  Random  r  =  new  Random();

  int  M  =  (int)numericUpDown2.Value;

  progressBar1.Maximum  =  M-1;

  double  sumbest  =  double.PositiveInfinity;

  int[]  pbest  =  new  int[N];

  for  (int  m  =  0;  m  <  M;  m++)

{

  int[]  p  =  new  int[N];

  for  (int  i  =  0;  i  <  N;  i++)

  p[i]  =  i;

for  (int  i  =  1;  i  <  N;  i++)

  {

  int  j  =  r.Next(1,  N);

  int  t  =  p[i];

  p[i]  =  p[j];

  p[j]  =  t;

  }

Предположим,  что  остальные  вершины  появились  в  порядке  i₁  i₂  i₃  i_n  где  i_k  —  номер  вершины  при  k-ом  выборе.  Получим  гамильтонов  контур:

Посчитаем  длину  этого  контура  и  запомним  ее.  Повторим  эту  процедуру  еще  раз  и  сравним  полученные  результаты,  выбрав  наименьший,  и  запомним  только  его  [1,  с.  80]  В  нашей  программе  это  выглядит  так:

if  (sum  <  sumbest)

  {

  sumbest  =  sum;

  pbest  =  p;

  }

progressBar1.Value  =  m;

  }

  textBox1.Text  =  textBox1.Text  +  "Минимальный  путь:  1";

  for  (int  i  =  1;  i  <  N;  i++)

  textBox1.Text  =  textBox1.Text  +  "->"  +  (pbest[i]  +  1);

  textBox1.Text  =  textBox1.Text  +  "\r\nСуммарное  расстояние:  "  +  sumbest  +  "\r\n";

  }

private  void  Form1_Load(object  sender,  EventArgs  e)

  {

  numericUpDown1_ValueChanged(sender,  e);

  button1_Click(sender,  e);

  }

  } 

  double  sum  =  0;

  for  (int  i  =  0;  i  <  N  -  1;  i++)

  if  (A[p[i],  p[i  +  1]]  ==  0  ||  sum  >  sumbest)

  {

  sum  =  double.PositiveInfinity;

  break;

  }

  else

  sum  =  sum  +  A[p[i],  p[i  +  1]];

if  (A[p[N  -  1],  p[0]]  ==  0)

  sum  =  double.PositiveInfinity;

  else

  sum  =  sum  +  A[p[N  -  1],  p[0]];

  if  (sum  <  sumbest)

  {

  sumbest  =  sum;

  pbest  =  p;

  }

В  заключение,  хотелось  бы  добавить,  что  вышеприведенный  алгоритм  был  протестирован  по  следующим  параметрам:  количество  городов,  количество  попыток  и  количество  верных  ответов  при  прохождении  программы  100  раз. 

Данные  занесены  в  таблицу: 

Таблица  1.

Результаты  тестирования  алгоритма

Основываясь  на  результатах,  представленных  в  таблице,  можно  сделать  вывод  о  том,  что  применение  метода  Монте-Карло  дает  оптимальное  решение  в  большинстве  случаев,  если  количество  попыток  превосходит  1000. 

Список  литературы:

1.Акимов  О.Е.  Дискретная  математика.  Логика,  группы,  графы.  М.:  Лаборатория  базовых  знаний,  2003.  —  376  с.

2.Степанов  В.Н.  Дискретная  математика:  графы  и  алгоритмы  на  графах.  Омск:  Издательство  ОмГТУ,  2010.  —  116  с.