Статья опубликована в рамках: XIV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 28 ноября 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
"За статью проголосовало 0 человек"
АППРОКСИМАЦИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ЭЛЛИПТИЧЕСКОГО ОПЕРАТОРА МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Хабибулина Татьяна Васильевна
студент 5 курса, кафедра информатики и вычислительной техники
ПГУ им. Шолом-Алейхема, РФ, Еврейская автономная область, г. Биробиджан
E-mail: Habik_tania@mail.ru
Бабинер Елена Станиславовна
научный руководитель, старший преподаватель кафедры высшей математики и методики обучения математике ПГУ им. Шолом-Алейхема, Еврейская автономная область, г. Биробиджан
Пусть ![]() ограниченная область с кусочно-гладкой границей
ограниченная область с кусочно-гладкой границей ![]() . Введем обозначения:
. Введем обозначения: ![]() и
и ![]() — пространства Соболева,
— пространства Соболева, ![]() множество всех финитных в
множество всех финитных в ![]() функций из
функций из ![]() .
.
Задача Дирихле. Рассмотрим первую краевую задачу:
![]() , (1)
, (1)
![]() . (2)
. (2)
Слабое решение задачи (1), (2) реализует минимум функционала ![]() на
на ![]() [6, с. 300], где
[6, с. 300], где
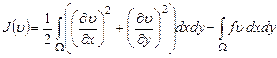 .
.
Задача Неймана. Уравнение (1) и краевые условия:
![]() . (3)
. (3)
Условия (3) относятся к естественными краевыми условиями [4, 10]. Задача Неймана с однородными краевыми условиями (3) порождает не положительный оператор, поэтому имеет единственное решение при ![]() . Слабое решение задачи (1), (3) реализует минимум функционала
. Слабое решение задачи (1), (3) реализует минимум функционала ![]() на
на ![]() [5, с. 320].
[5, с. 320].
Задача Синьорини. Уравнение (1) и краевые условия Синьорини [1, 7]:
![]() ,
, ![]() ,
, ![]() на
на ![]() , (4)
, (4)
где ![]() производная по внешней нормали к границе
производная по внешней нормали к границе ![]() . Определим множество
. Определим множество ![]() , которое является замкнутым выпуклым подмножеством
, которое является замкнутым выпуклым подмножеством ![]() [2, 15]:
[2, 15]:
![]() . (5)
. (5)
Слабое решение задачи (1), (4) реализует минимум функционала ![]() на
на ![]() [6, 20].
[6, 20].
Рассмотрим аппроксимацию этих задач на трапециевидной области с углом ![]() методом конечных элементов (МКЭ). Триангуляция области с шагами
методом конечных элементов (МКЭ). Триангуляция области с шагами ![]() ,
, ![]() ,
, ![]() (
(![]() количество разбиений по
количество разбиений по ![]() ,
, ![]() количество разбиений по
количество разбиений по ![]() ), виды конечных элементов с нумерацией носителей для прямоугольной (прямые цифры), треугольной (наклонные цифры) частей и их границы соединения представлены на рисунке 1.
), виды конечных элементов с нумерацией носителей для прямоугольной (прямые цифры), треугольной (наклонные цифры) частей и их границы соединения представлены на рисунке 1.
Приближенное решение ![]() ищем в виде линейной комбинации:
ищем в виде линейной комбинации:
![]() , (6)
, (6)
где: ![]() кусочно-линейные финитные (базисные) функции, заданные в узлах сетки.
кусочно-линейные финитные (базисные) функции, заданные в узлах сетки.
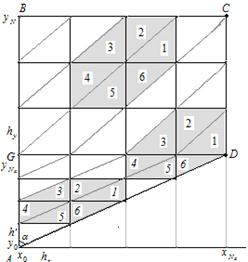
Рисунок 1. Триангуляция области ![]()
Вид базисных функций для прямоугольной области [4, с. 184]:
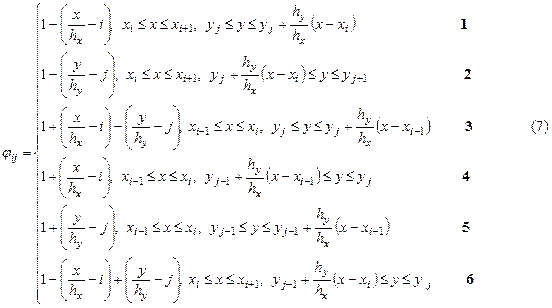
для треугольной части области:

Для границы соединения прямоугольной и треугольной частей области вид базисных функций ![]() определяется следующим образом: для носителей 1, 2 и 3 аналитическое задание совпадает с заданием на соответствующих носителях в
определяется следующим образом: для носителей 1, 2 и 3 аналитическое задание совпадает с заданием на соответствующих носителях в ![]() , а для носителей 4, 5 и 6 — в
, а для носителей 4, 5 и 6 — в ![]() .
.
Подставляем линейную комбинацию (6) в функционал ![]() , предварительно введя обозначения
, предварительно введя обозначения 
![]() , получаем:
, получаем:
![]() (9)
(9)
Матрица ![]() называется матрицей жесткости. Чтобы показать ее вид, ограничимся для примера 18 узлами в сетке, то есть для
называется матрицей жесткости. Чтобы показать ее вид, ограничимся для примера 18 узлами в сетке, то есть для ![]() (прочерк в ячейке матрицы означает отсутствие узла в сетке с таким номером) (рис. 2).
(прочерк в ячейке матрицы означает отсутствие узла в сетке с таким номером) (рис. 2).
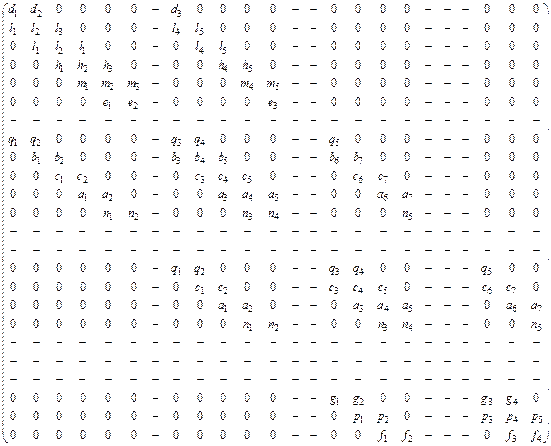
Рисунок 2. Матрица жесткости
Элементы представленной матрицы жесткости рассчитываются по следующим формулам:
Внутренние точки |
||
Прямоугольная область |
||
|
||
Треугольная область |
||
|
||
Граница изменения области |
||
|
||
Углы |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При численном решении задач Дирихле и Неймана в соответствии с необходимым и достаточным условием существования экстремума выпуклого функционала, находим вариацию функционала (9) и приравниваем ее к нулю:
![]() (10)
(10)
Таким образом, получаем систему уравнений:
 (11)
(11)
Система (11) в развернутом виде:
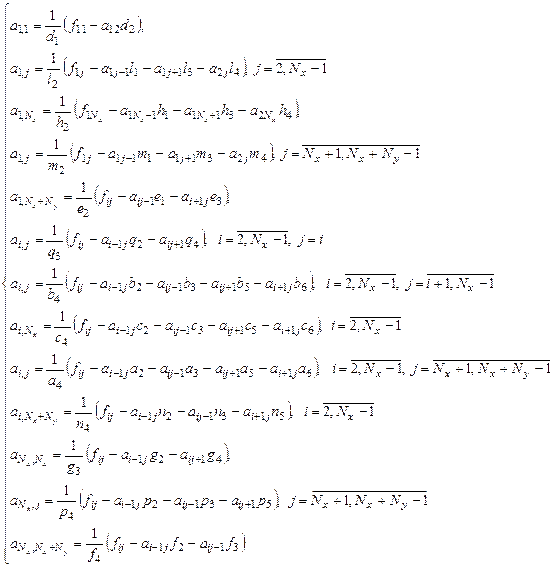
Для задачи Дирихле система (11) имеет вид:
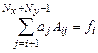 (12)
(12)
Развернутый вид системы (12):
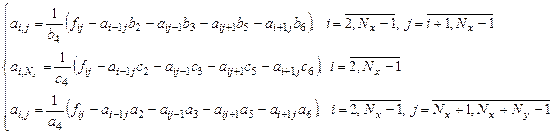
При решении систем применяется метод Зейделя.
Для отыскания минимума квадратичного функционала ![]() в задаче Синьорини применяется обобщение метода верхней релаксации [2, с. 82] с оператором проектирования
в задаче Синьорини применяется обобщение метода верхней релаксации [2, с. 82] с оператором проектирования ![]() , где
, где
![]() .
.
Зная ![]() , уточнение приближения
, уточнение приближения ![]() проводится по следующей схеме:
проводится по следующей схеме:
· для внутренних узлов
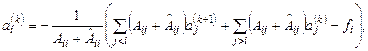
· для граничных узлов
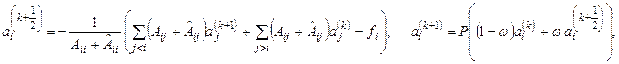
где ![]() — параметр релаксации, подходящий выбор которого ускоряет сходимость последовательности
— параметр релаксации, подходящий выбор которого ускоряет сходимость последовательности ![]() к точке минимума функционала.
к точке минимума функционала.
Результаты реализации описанных алгоритмов на трапециевидной области с углом ![]() представлены в таблице 1, где
представлены в таблице 1, где ![]() — количество итераций,
— количество итераций, ![]() — заданная точность.
— заданная точность.
Таблица 1.
Результаты численного решения
|
Задача |
|
|
|
|
|
|
Дирихле |
|
441 |
0,05 |
0,0001 |
140 |
|
Нейман |
|
441 |
0,05 |
0,001 |
76 |
|
Синьорини |
|
441 |
0,05 |
0,0001 |
21 |
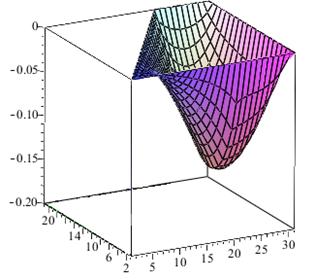
Рисунок 3. График решения задачи Дирихле
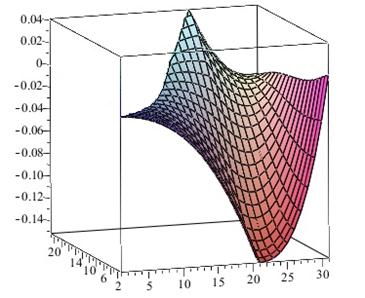
Рисунок 4. График решения задачи Неймана
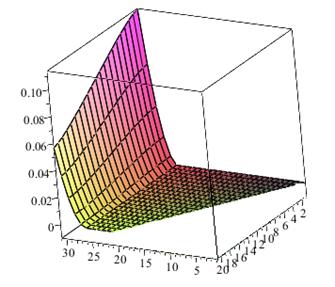
Рисунок 5. График решения задачи Синьорини
Список литературы:
1.Главачек И., Гаслингер Я., Нечас И., Ловишек Я. Решение вариационных неравенств в механике. М.: Мир, 1986. — 270 с.
2.Гловински Р., Лионс Ж.-Л., Тремольер Р. Численное исследование вариационных неравенств. М.: Мир, 1979. — 576 с
3.Дюво Г., Лионс Ж.-Л. Неравенства в механике и физике. М.: Наука, 1980. — 384 с.
4.Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. М.: Наука. Главная редакция физико-математической литературы, 1981. — 416 с.
5.Михлин С.Г. Линейные уравнения в частных производных. Учеб. пособие для вузов. М., «Высш. школа», 1977. — 431 с.
6.Намм Р.В. Введение в теорию и методы решения вариационных неравенств: Учебное пособие Хабаровск: Изд-во Хабар. гос. тех. ун-та, 1999. — 71 с.
дипломов


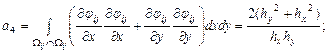
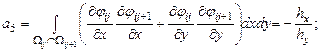
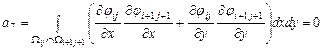
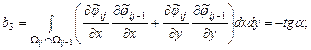
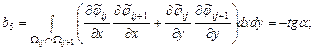
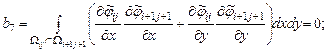

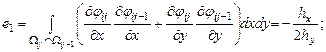
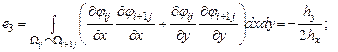
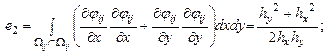
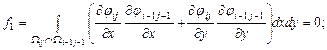

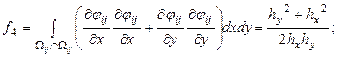

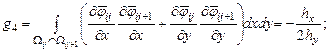
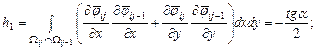
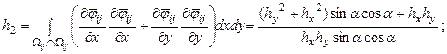
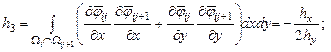
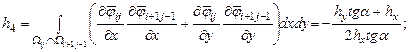
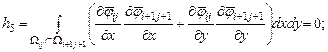
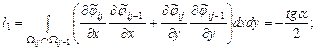
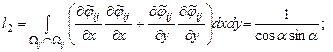
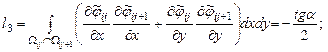
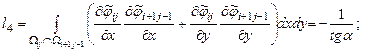


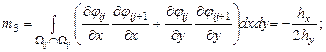
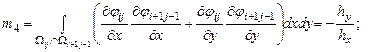
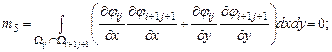

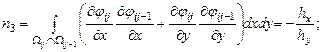

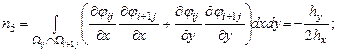
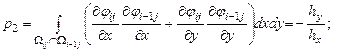
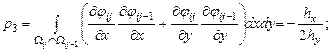
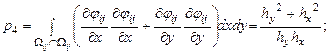
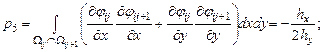
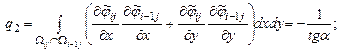



Оставить комментарий