Статья опубликована в рамках: II Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 16 апреля 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Часть I, Часть II, Часть III, Часть IV, Часть V
дипломов
МОДЕЛИРОВАНИЕ ТЕПЛОПЕРЕНОСА В ТВЕРДЫХ НЕМЕТАЛЛИЧЕСКИХ МАТЕРИАЛАХ И ИЗДЕЛИЯХ
Попов Валентин Дмитриевич
Студент 4 курса, кафедра «ГиТ» ФГБОУ ВПО «ТГТУ», г. Тамбов
E-mail: teplotehnika@nnn.tstu.ru
Бучнев Сергей Александрович
Студент 4 курса, кафедра «ГиТ» ФГБОУ ВПО «ТГТУ», г. Тамбов
E-mail: teplotehnika@nnn.tstu.ru
Фомин Антон Александрович
Студент 4 курса, кафедра «ГиТ» ФГБОУ ВПО «ТГТУ», г. Тамбов
E-mail: teplotehnika@nnn.tstu.ru
Кацуба Дарья Сергеевна
Студентка 5 курса, кафедра «ГиТ» ФГБОУ ВПО «ТГТУ», г. Тамбов
E-mail: teplotehnika@nnn.tstu.ru
Майникова Нина Филипповна
научный руководитель, д.т.н., профессор ФГБОУ ВПО «ТГТУ», г. Тамбов
Сложность и большой объем экспериментальных исследований по определению качества, долговечности и надежности изделий, как из традиционных, так и вновь синтезируемых материалов, требуют создания новых эффективных методов и средств контроля. Среди них особое место занимают тепловые методы неразрушающего контроля (НК) и диагностики.
Реализация контактного метода НК ТФС усложнена тем, что тепловое воздействие и получение измерительной информации в ходе эксперимента возможно осуществлять только на ограниченном участке поверхности исследуемого объекта. Поэтому наиболее важной и сложной задачей при создании теплового метода НК ТФС является разработка математической модели, адекватно описывающей реальный процесс теплопереноса в объекте исследования.
Академиком А.В. Лыковым доказано, что регулярные тепловые режимы первого и второго рода имеют общее свойство, характеризующееся независимостью от времени отношения теплового потока в любой точке тела к потоку тепла на его поверхности. Математическая модель, описывающая термограмму, в данном случае чаще всего является линейной по параметрам или легко линеаризуется. Однако основная часть этих методов базируется на моделях для тел конечных размеров (пластина, цилиндр, шар). В то время как большая часть методов НК базируется на моделях полупространств (плоского, цилиндрического, сферического) [1, 2].
Применительно к таким моделям следует говорить не о регулярном тепловом режиме для всего тела (так как оно принимается неограниченным), а о регуляризации теплового процесса только для какой-то определенной области тела. Следовательно, основываясь только на участках термограммы, соответствующих регуляризации теплового режима в области нагревателей и термоприемников, то, во-первых, расчетные соотношения будут более простыми и во многих случаях линейными по параметрам, во-вторых, систематические составляющие погрешности будут либо значительно меньшими, чем случайные, либо будут носить постоянный характер, т. е. не зависеть от времени.
Таким образом, проблема разработки нового метода НК твердых неметаллических материалов как на стадии технологического контроля в процессе их производства, так и в процессе эксплуатации изделий из них, является важной и актуальной.
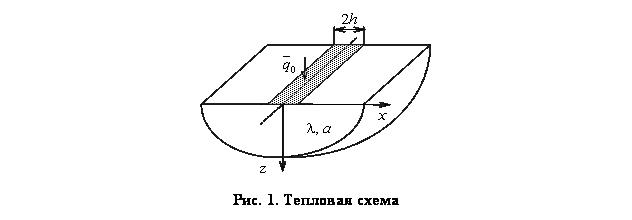
Рассмотрим тепловую схему, представленную на рис. 1. На поверхности полуограниченного в тепловом отношении тела расположен нагреватель в виде полосы шириной 2h, через которую в материал подается тепловой поток ![]() [3].
[3].
Математическая модель распределения тепла в рассматриваемой системе (рис. 1) может быть записана в виде прямой задачи теплопроводности:
 ; (1)
; (1)
![]() ; (2)
; (2)
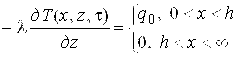 ; (3)
; (3)
![]() ; (4)
; (4)
![]() , (5)
, (5)
где ![]() – температурное поле исследуемого тела точках с координатами х в моменты времени τ; h– ширина нагревателя;
– температурное поле исследуемого тела точках с координатами х в моменты времени τ; h– ширина нагревателя; ![]() – тепловой поток, подводимый к свободной поверхности исследуемого тела; λ и а – теплопроводность и температуропроводность, соответственно, исследуемого тела.
– тепловой поток, подводимый к свободной поверхности исследуемого тела; λ и а – теплопроводность и температуропроводность, соответственно, исследуемого тела.
Решение краевой задачи теплопроводности (1) – (5) имеет следующий вид [2, 3]:
 (6)
(6)
где τ – время, с; х– координата, м.
Температура тела зависит от большого числа переменных и постоянных параметров. Это обстоятельство затрудняет численные расчеты. Становится весьма сложным привести результаты расчета в определенную систему, уловить влияние отдельных факторов на течение процесса. Задача значительно облегчается, когда размерные переменные объединяются в безразмерные комплексы (критерии).
Введем следующие обозначения:
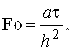
![]()
 (7) – (9)
(7) – (9)
где ![]() – безразмерное время (число Фурье);
– безразмерное время (число Фурье); ![]() и
и ![]() – безразмерные координаты;
– безразмерные координаты; ![]() – значение температуры в безразмерном представлении.
– значение температуры в безразмерном представлении.
Сведем выражение (1) к безразмерному виду:
 (10)
(10)
где ![]() – время, в безразмерном представлении;
– время, в безразмерном представлении; ![]() – безразмерная координата;
– безразмерная координата; ![]() – температура, в безразмерном представлении.
– температура, в безразмерном представлении.
Для точки с координатами (0; 0) выражение (2) примет вид
 . (11)
. (11)
Используя следующие соотношения:
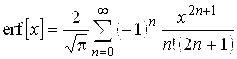 ,
,  ,
,
получим выражение для температуры поверхности z = 0 в точке с координатой x для больших значений t:
 , (12)
, (12)
где γ – число Эйлера.
Выражение (12) в безразмерной форме применительно к точкес координатами (0; 0) для больших значений t имеет вид:
![]() . (13)
. (13)
Найденное выражение (13) автоматически распространяется на бесконечное множество тепловых явлений применительно к схеме, представленной на рис. 1.
Измерительная схема метода с линейным плоским нагревателем постоянной мощности представлена на рис. 2.
Рассмотрим два тела (1 и 2) с различными теплофизическими свойствами (λ1, а1 и λ2, а2). Размеры первого тела: длина – l1; толщина – d1; ширина – 2H1. Размеры второго тела: длина – l2; толщина – d2; ширина – 2H2. В плоскости контакта действует линейный источник тепла в виде полосы. Первое тело представляет собой исследуемое изделие. Второе тело – подложка измерительного зонда (ИЗ). Начальная температура тел одинакова и равна Т0. Источник тепла начинает действовать в начальный момент времени (τ = 0). В месте соприкосновения поверхностей тел 1 и 2 (рис. 2) с нагревателем осуществляется идеальный тепловой контакт. Перед тепловым воздействием измеряют разность температур между двумя точками, первая из которых располагается в непосредственной близости от нагревателя, а вторая – на расстоянии d2 от него, до тех пор, пока эта разность температур не станет меньше наперед заданной величины.
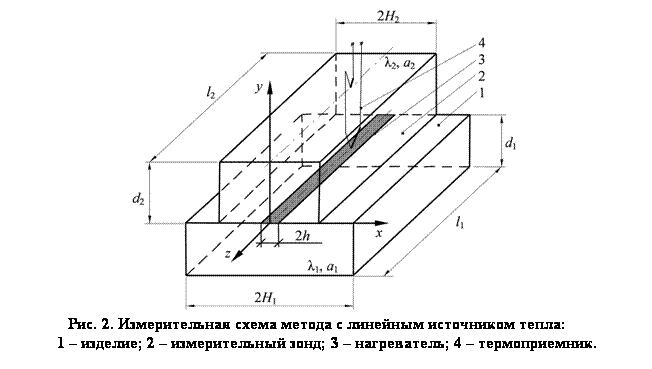
Тепловое воздействие осуществляется подавая на нагреватель электрический ток, мощность нагревателя – ![]() . В ходе эксперимента фиксируется термограмма – зависимость разности температур (Т) в точках контроля от времени (τ) [3].
. В ходе эксперимента фиксируется термограмма – зависимость разности температур (Т) в точках контроля от времени (τ) [3].
На рис. 3 представлены термограммы Θ = f(Fo).
Кривая 1 получена численным решением задачи при соотношении ![]() с помощью пакета ELCUT [4]. Кривые 2 и 3 получены по выражениям (11) и (13) с помощью пакета Maple [5].
с помощью пакета ELCUT [4]. Кривые 2 и 3 получены по выражениям (11) и (13) с помощью пакета Maple [5].
На термограммах, представленных на рис. 3, выделены три участка: I, II и III.
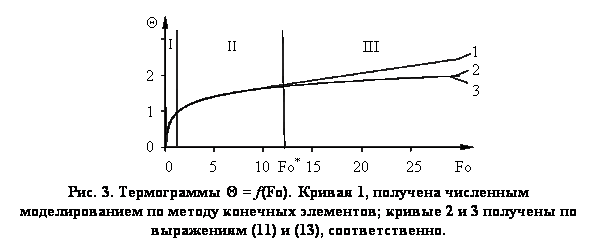
Первый (I) участок термограммы характеризуется тем, что тепловой поток, проходящий через точку контроля, является переменным во времени и соответствует начальной стадии развития теплового процесса.
Второй (II) участок термограммы характеризуется регуляризацией теплового режима в локальной области нагревателя и термоприемника (рис. 2) тепловой поток, проходящий через точку контроля, становится практически постоянным. Это позволяет использовать математическую модель (13) описания процесса теплопереноса для второго (рабочего) участка термограммы.
Третий (III) участок термограммы характеризуется тем, что нарушается условие полуограниченности объекта исследования (тепловой поток, проходящий через точку контроля, вновь становится переменным).
Графические зависимости Θ = f(Fo), полученные по формулам (11) и (13), а также численные решения для соотношений ![]() собраны в семейство, представленное на рис. 4. Выделим рабочие участки на термограммах (на которых исследуемое тело можно считать полуограниченным).
собраны в семейство, представленное на рис. 4. Выделим рабочие участки на термограммах (на которых исследуемое тело можно считать полуограниченным).
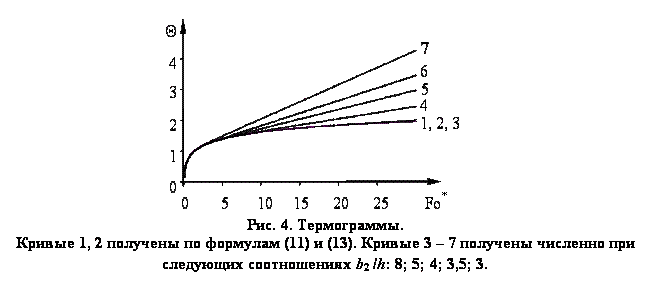
Зная границы рабочих участков термограмм для различных соотношений ![]() , найдена зависимость
, найдена зависимость ![]() (рис. 5). По оси ординат на рис 5 представлены значения Fo*, соответствующие времени окончания второго (II) рабочего участка, на термограммах (1 – 7).
(рис. 5). По оси ординат на рис 5 представлены значения Fo*, соответствующие времени окончания второго (II) рабочего участка, на термограммах (1 – 7).
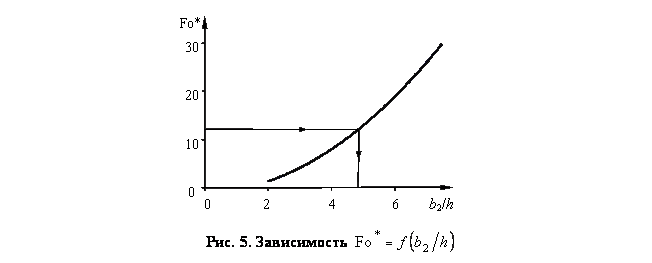
Зависимость, представленная на рис. 5, позволяет определить размеры подложки измерительного зонда. Например, при Fo* = 12,3 толщина подложки измерительного зонда должна быть b2 ≥ 4,85 мм.
Рассмотрим применение данного подхода при реализации разработанного метода определения теплофизических свойств полимерных материалов (ПМ).
Известно, что теплопроводность полимеров λ находится в пределах 0,2 – 0,8 Вт/(м·°С). Следовательно, тепловой поток, которым должно осуществляться воздействие на образец, должен быть не одинаков для различных образцов ПМ.
В выражении (6) значение безразмерной температуры можно выразить следующей зависимостью:
![]() . (14)
. (14)
Помимо теплового потока ![]() и теплопроводности λ в выражение (20) входят: температура T поверхности в момент времени t и безразмерная температура Θ. Нагрев исследуемой точки поверхности для различных ПМ (в зависимости от их теплопроводности) предлагается осуществлять на величинуΔT = 10 – 20 °С. Причем, для наиболее теплопроводных материалов значение ΔT следует назначать равным 10 °С. Численное значение безразмерной температуры найдем из выражения (13). Например, при Fo*=12,3
и теплопроводности λ в выражение (20) входят: температура T поверхности в момент времени t и безразмерная температура Θ. Нагрев исследуемой точки поверхности для различных ПМ (в зависимости от их теплопроводности) предлагается осуществлять на величинуΔT = 10 – 20 °С. Причем, для наиболее теплопроводных материалов значение ΔT следует назначать равным 10 °С. Численное значение безразмерной температуры найдем из выражения (13). Например, при Fo*=12,3
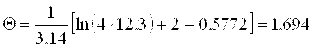 .
.
Для ΔT=10 °С значение ![]() :
:
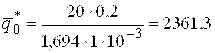 Вт/м2.
Вт/м2.
Сопротивление нагревателя:
 (15)
(15)
где U – напряжение, равное 20 В; Q – тепловая мощность, Вт; ![]() ;
;![]() – тепловой поток, Вт/м2; S – площадь плоского линейного нагревателя, м2;
– тепловой поток, Вт/м2; S – площадь плоского линейного нагревателя, м2; ![]() ; 2h – ширина полосы, равная, например, 0,002 м; l – длина полосы, равная, например, 0,05 м.
; 2h – ширина полосы, равная, например, 0,002 м; l – длина полосы, равная, например, 0,05 м.
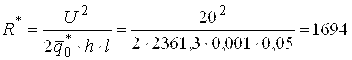 Ом.
Ом.
Аналогично определены тепловой поток и сопротивление нагревателя для величины перегрева ΔT=20 °С: ![]() Вт/м2 и
Вт/м2 и ![]() Ом.
Ом.
Из приведенных данных следует, что в зависимости от значения теплопроводности ПМ тепловой поток следует назначать в интервале значений 2361,3 – 4722,6 Вт/м2, а сопротивление нагревателя при этом изменяетсяв интервале значений 847 – 1694 Ом.
Оптимальный временной интервал проведения измерений будет зависеть от значения температуропроводности исследуемого ПМ. Согласно справочным данным температуропроводность ПМ находится в интервале, а = (0,01 – 0,5)∙10-6 м2/с.
Из выражения:
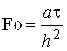 ,
,
определены значения времени (![]() и
и ![]() ), соответствующие длительности эксперимента при исследованиях полимерных материалов с заявленными значениями температуропроводности.
), соответствующие длительности эксперимента при исследованиях полимерных материалов с заявленными значениями температуропроводности.
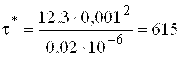 с;
с; 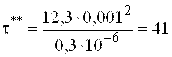 с.
с.
Следовательно, длительность эксперимента при исследованиях ПМ составит от ![]() = 41 до
= 41 до ![]() = 615 с.
= 615 с.
Выводы
1. Исследована математическая модель распространения тепла в твердых неметаллических телах от действия плоского линейного источника тепла постоянной мощности при регуляризации тепловых потоков в локальных областях.
2. Разработана методика определения оптимальных условий НК ТФС.
3. Численным методом определены оптимальные условия НК ТФС полимерных материалов.
Список литературы:
1. Лыков, А.В. Теория теплопроводности / А.В. Лыков. – М.: Высш. шк., 1967. – 599 с.
2. Карслоу, Г. Теплопроводность твердых тел / Г. Карслоу, Д. Егер. – М.: Наука, 1964. – 487 с.
3. Жуков, Н.П. Многомодельные методы и средства неразрушающего контроля теплофизических свойств твердых материалов и изделий. / Н.П. Жуков, Н.Ф. Майникова // Монография. – М.: Машиностроение – 1, 2004. – 288 с.
4. ELCUT: моделирование двухмерных полей методом конечных элементов. Версия 5.5. Руководство пользователя. – СПб.: Производственный кооператив ТОР, 2003. – 249 с.
5. Сдвижков, О.А. Математика на компьютере: Maple 8 / О.А. Сдвижков – М.: СОЛОН-Пресс, 2003. — 176 с.
дипломов


Оставить комментарий