Статья опубликована в рамках: II Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 16 апреля 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Часть I, Часть II, Часть III, Часть IV, Часть V
дипломов
ПРИМЕНЕНИЕ МЕТОДОВ ЛОГИСТИКИ ПРИ ОПТИМИЗАЦИИ РАСПРЕДЕЛЕНИЯ МАТЕРИАЛЬНЫХ РЕСУРСОВ
Абдуллин Асет Нигматуллаевич
студент 4-курса, кафедра информационных систем
ЮКГУ им. Ауезова М., г. Шымкент
E-mail: 250ikhb@mail.ru
Исмаилов Хайрулла Бахтиярович
научный руководитель, канд. техн. наук, ст.преподаватель ЮКГУ им. Ауезова М., г. Шымкент
За последние десятилетия усилилось негативное влияние производственных (в особенности, химических) факторов на население, производственную и социальную инфраструктуру и экологическую систему, увеличился риск возникновения чрезвычайных ситуаций техногенного характера (ЧС ТХ) на потенциально опасных химических предприятиях различной организационно-правовой формы и формы собственности. Для устранения вышеприведенных опасностей, приоритетными направлениями в области обеспечения химической и биологической безопасности должны стать: совершенствование государственного регулирования и нормативно-правовой базы; развитие промышленной политики; использование успехов фундаментальной и прикладной науки, технологий и техники; предупреждение чрезвычайных ситуаций и ликвидация их последствий; подготовка и повышение квалификации кадров. Решение этих задач достигается путем создания государственной системы обеспечения химической и биологической безопасности Республики Казахстан (как подсистемы единой государственной системы предупреждения и ликвидации чрезвычайных ситуаций), предусматривающей категорирование, прогнозирование, предупреждение и парирование угроз химической безопасности, ликвидацию последствий чрезвычайных ситуаций в результате воздействия химических, а также биологических факторов.
Разработка мер технологического и управленческого характера, направленных на уменьшение риска ЧС ТХ и ликвидации их последствий требует привлечения огромного материального и информационного ресурса. Решение этой проблемы требует учета большого числа параметров: экономических (необходимые ресурсы по ликвидации аварий на промпредприятиях, транспортные средства, материалы и т. д.), информационных (создание соответствующих баз данных по химически опасным веществам, методики расчета и компьютерных программ и т. д.), организационно-управленческих (перераспределение материальных ресурсов при крупномасштабных катастрофах, повышение квалификации сотрудников и т. д.). Оптимальное варьирование материально-техническими и информационными ресурсами возможно при применении современных методов и представлений соответствующего научного направления логистики.
В экономических задачах методы логистики развиты достаточно и с успехом применяются на практике. Учеными разных направлений разработаны эффективные методики рационального управления распределением материальных и информационных ресурсов. В России, Германии, Франции, Казахстане и др. странах имеются определенные разработки и научно-технический потенциал, направленные на решение аналогичных задач. Однако эти результаты не адаптированы к решению задач повышения промышленной безопасности, не учитывают специфику и необходимости оперативного реагирования соответствующих структур и государственных органов на снижение риска ЧС ТХ и уменьшения их вредных последствий.
Поэтому, разработка подсистем интегрированной логистики по мониторингу и моделированию причин и последствий чрезвычайных ситуаций техногенного характера и внедрение их в практике деятельности МЧС является
Рассмотрим задачу оптимального распределения материальных ресурсов. Пусть имеется т складов хранения n материальных ресурсов, необходимых для ликвидации последствий ЧС ТХ. Ставится задача составления математической модели распределения этих ресурсов по пунктам назначения с последующей ее реализацией [1].
Введем следующие обозначения:
i – номер склада;
j – номер материального ресурса;
![]() - количество j - ресурса в i – складе, штук;
- количество j - ресурса в i – складе, штук;
![]() - стоимость доставки j - ресурса с i – склада в место аварии, тенге;
- стоимость доставки j - ресурса с i – склада в место аварии, тенге;
![]() - потребность в j – ресурсе при ЧС ТХ, штук;
- потребность в j – ресурсе при ЧС ТХ, штук;
![]() - время доставки ресурсов в i – пункт, час;
- время доставки ресурсов в i – пункт, час;
![]() - допустимое время доставки j – ресурса; час;
- допустимое время доставки j – ресурса; час;
![]() - определяемое необходимое количество j – ресурса с i – склада, штук;
- определяемое необходимое количество j – ресурса с i – склада, штук;
При этом должны выполняться следующие ограничения: для всех значений i, j имеет место
![]() и
и ![]() . (1)
. (1)
Учитывая эти ограничения, в первом приближении целевая функция будет иметь следующий вид:
![]() . (2)
. (2)
Это означает, что затраты, необходимые для доставки материальных ресурсов, должны быть минимальными.
Схематически данную задачу в общем виде можно представить в виде рисунка 1.
Из рисунка 1 видно, что всевозможные доставки из i – склада j – материального ресурса могут осуществляться ![]() способами. Кроме того, если заранее известно, что в каком-то складе некоторого материального ресурса нет, то принимается
способами. Кроме того, если заранее известно, что в каком-то складе некоторого материального ресурса нет, то принимается ![]() =0.
=0.
Задача состоит в том, чтобы минимизировать функцию (2) при ограничениях (1).
Рассмотрим данную задачу в наиболее общей постановке, т. е. для нескольких пунктов распределения. Транспортная таблица для данной задачи приведена в таблице 1.
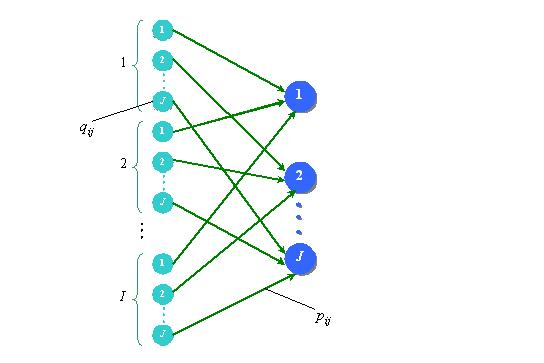
Рисунок 1. Схема сбора необходимых материальных ресурсов из складов для ликвидации ЧС ТХ
В данной таблице перевозок некоторые маршруты недопустимы, поскольку в данной постановке задачи ресурсы не могут заменить друг друга. Например, нельзя осуществлять перевозки из пункта хранения материалов марки M1 в пункт доставки товаров модели М2. В данной таблице запрещенным маршрутам соответствует очень высокая стоимость М (рij = M).
Для того чтобы учесть многопродуктовый характер задачи, изменим транспортную модель следующим образом: разобьем склады на несколько пунктов расположения в соответствии с числом моделей ресурсов, хранимых в этом складе. Аналогично поступим и с пунктом назначения, т.е. будем считать, что каждый пункт назначения состоит из m подпунктов, соответствующих т моделям ресурсов. В результате получим ![]() исходных пунктов и n пунктов назначения. Представим данные в виде транспортных матриц (таблица 2).
исходных пунктов и n пунктов назначения. Представим данные в виде транспортных матриц (таблица 2).
Таблица 1.
Транспортная таблица для задачи в общей постановке
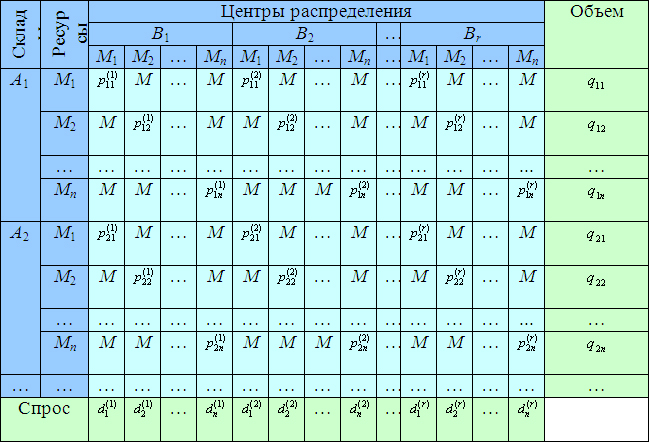
Таблица 2
Транспортные таблицы по видам материальных ресурсов
для М1:
Склады |
Центры распределения |
Объем производства |
|||
В1 |
В2 |
… |
Br |
||
А1 |
|
|
… |
|
|
А2 |
|
|
… |
|
|
… |
… |
… |
… |
… |
… |
Ат |
|
|
… |
|
|
Спрос |
|
|
… |
|
|
и т. д.
Рассмотрение этих n моделей дает решение, совпадающее с оптимальным решением задачи, соответствующей первоначальной таблице. С вычислительной точки зрения небольшие подзадачи решить существенно эффективнее, чем одну сложную задачу. Возможность разбиения таблицы на части обусловлена полной независимостью различных товаров. В результате деления первоначальной таблицы получили п – однопродуктовых транспортных задач. В случае незамкнутости одной из моделей добавляется фиктивный склад или пункт приема.
Введем дополнительные коэффициенты.
Пусть ![]() - емкость транспортного канала, который соединяет i – пункт с местом аварий, т.е. транспортная возможность каждого пункта (ед.),
- емкость транспортного канала, который соединяет i – пункт с местом аварий, т.е. транспортная возможность каждого пункта (ед.), ![]() - занимаемое место в единице транспорта одним j – ресурсом. Тогда должно выполняться следующее дополнительное ограничение:
- занимаемое место в единице транспорта одним j – ресурсом. Тогда должно выполняться следующее дополнительное ограничение:
![]() . (3)
. (3)
Для определения количества транспортных рейсов, необходимых для обеспечения ![]() потребности, добавим в
потребности, добавим в ![]() индекс k.
индекс k. ![]() будет определять необходимое количество j – ресурса с i – склада при k – рейсе. Тогда условия ограничений примут вид:
будет определять необходимое количество j – ресурса с i – склада при k – рейсе. Тогда условия ограничений примут вид:
![]() для
для ![]() , (4)
, (4)
![]() для
для ![]() , (5)
, (5)
В эту модель необходимо добавить оптимизационное условие времени, т.е. условие для минимизации промежутка времени, необходимое для доставки материальных ресурсов из складов в место ЧС ТХ. Это условие в общем виде можно представить в следующем виде:
![]() для любых j. (6)
для любых j. (6)
Функция времени ![]() также зависит от k, и будет определяться как
также зависит от k, и будет определяться как
![]() . (7)
. (7)
Это обусловлено тем, что на время доставки и на следующий рейс также входит время возвращения в склад. Кроме того, должно выполняться условие
![]() для
для ![]() (8)
(8)
или с учетом (7)
![]() . (9)
. (9)
Для определения количества осуществляемых рейсов с каждого склада преобразуем формулу (9):
 , (10)
, (10)
т.е. округление до целого производится в меньшую сторону.
Таким образом, получена следующая задача:
Минимизировать следующую целевую функцию
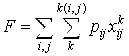 (11)
(11)
при следующих ограничениях:
 ,
, ![]() ,
, ![]() , (12)
, (12)
 ,
, ![]() , (13)
, (13)
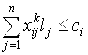 ,
, ![]() ,
, ![]() , (14)
, (14)
предварительно определив транспортные рейсы каждого склада по формуле (10).
Эта задача является задачей линейного программирования, но с дополнительными условиями и ограничениями для времени и возможностей складов [2]. Решением данной модели можно получить конкретные значения целевой функции при различных исходных данных и ограничениях.
Для автоматизации расчета значения целевой функции и ее составляющих нами разработана информационная система, позволяющая проводить вычисления для широкого диапазона входных данных и ограничений. Интерфейс информационной системы и назначения ее окон представлены ниже.
После запуска программы система запросит пароль для доступа к работе (рисунок 2):
Рисунок 2. Окно ввода пароля
В появившемся окне необходимо выбрать виды и количество ограничений, либо вкладку «Ввод данных об авариях» в строке меню окна (рисунок 3):
Рисунок 3. Главное окно информационной системы
После нажатия вышеназванной вкладки, в появившемся окне выбираются первоначальные исходные данные об авариях и материальных ресурсах (рисунок 4):
Рисунок 4. Ввод исходных данных об авариях и исходных данных
Задав требуемые данные, данное окно можно временно спрятать, либо продолжить работу с открытым окном. При этом автоматически формируется отчет для хранения решения данной задачи. В окне «Потребности в ресурсах» необходимо ввести количественные данные о материальных ресурсах для ликвидации каждой аварии (рисунок 4). Одной из особенностей этой системы является возможность ввода данных из сохраненных файлов, либо генерирование случайными числами в заданном диапазоне. Для примера воспользуемся автоматическим генерированием случайных чисел:
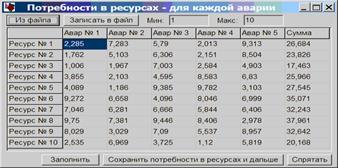
Рисунок5. Окно ввода данных о потребностях
В следующем шаге ввода исходных данных вводятся данные о времени доставки материальных ресурсов с каждого склада на места аварий (рисунок 6). Для ликвидации последствий ЧС каждый материальный ресурс должен быть доставлен за ограниченное время, после которого эффект от него может уменьшиться либо не пригодиться (рисунок 7).

Рисунок 6. Окно ввода данных о времени доставки ресурсов
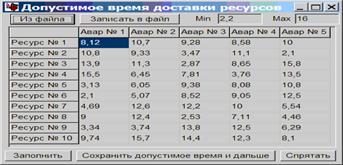
Рисунок 7. Окно ввода временных данных на доставку ресурсов
Главным элементом стандартной задачи линейного программирования является ввод информацию о затратах, в частности транспортных, на доставку материальных ресурсов.
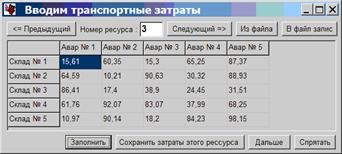
Рисунок 8. Окно ввода транспортных затрат на доставку
После заполнения всех вышепоказанных окон данными решение математической модели оформляется в виде рисунка 9. Выходными данными являются значения целевой функции и ее составляющих. Полный результат оформляется в виде файла, сохраняемого по усмотрению пользователя.

Рисунок 9. Окно вывода результатов
Разработанная математическая модель распределения позволяет управлять складскими материальными ресурсами и контролировать их объем при постоянных изменяющихся потребностях. Данная модель создана с использованием модифицированного метода решения транспортной задачи с дополнительными ограничениями и условиями на время. Результаты данной математической модели при конкретных числовых значениях входных данных хорошо согласуются с результатами разработанной компьютерной программы. Компьютерная программа разработана с использованием современных аппаратных и программных средств и позволяет решать задачи для широкого диапазона исходных данных.
Таким образом, созданы математическая модель и информационная система для расчета распределения материальных ресурсов и информационных потоков для ликвидации последствий ЧС техногенного характера. Для их реализации необходимы конкретные данные по чрезвычайным ситуациям
Список литературы:
- Гаджинский А. М. Основы логистики. - М.: ИВЦ МАРКЕТИНГ, 1997. -256 с.
- Гордон М. П. Проблемы комплексного управления товародвижением в материально-техническом снабжении. М.: НИИМС, 1993. - 200 с.
- Миротин Л. Б. Логистика интегрированных цепочек поставок. – М. : Экзамен, 2003. – 260 с.
дипломов


Оставить комментарий