УСТОЙЧИВОСТЬ ВЕРТИКАЛЬНОГО ЖЕСТКОГО НЕУРАВНОВЕШЕННОГО ГИРОСКОПИЧЕСКОГО РОТОРА С НЕЛИНЕЙНОЙ УПРУГОЙ ХАРАКТЕРИСТИКОЙ

Абукадыр Нурсултан

студент 2 курса, теплоэнергетический факультет, АУЭС, г Алматы

Е-mail: 

Искаков Жарилкасин

научный руководитель, канд. техн. наук, доцент АУЭС, г. Алматы

В настоящее время совместное влияние перекоса и дисбаланса массы диска на колебания и устойчивость ротора различной геометрии является одной из мало изученных проблем. В работе Бенсона [1] исследуется совместное действие перекоса и дисбаланса массы диска на установившиеся линейные колебания консольного ротора, в результате прецессирующий ротор будет иметь необычную фазово-частотную характеристику, причем фаза колебаний необязательно соответствовать ориентации дисбаланса на малых частотах вращения. Этот обстоятельство существенно изменяет методы балансировки ротора. В связи с тем, что в работе Бенсона внешнее демпфирование вводилось только в уравнения поступательного движения диска, она не могла дать точные выражения амплитуды и фазы колебаний с учетом внешнего трения. Это замечалось в бесконечном росте амплитуды колебаний при прохождении через вторую критическую скорость. Этот пробел учитывался в работе [2], где наряду с исследованием влияния двух и обобщенного дисбаланса на амплитудно – и фазово-частотные характеристики и остаточный фазовый угол двухопорного консольного ротора изучались зависимости резонансной амплитуды и остаточного угла сдвига по фазе от величины консольности вала и коэффициента внешнего демпфирования. Методы исследований работы [1, 2] использованы в работах [3, 4] для линейных и установившихся колебаний гироскопического и несимметричного роторов. В данной работе исследуется влияние угла между ориентациями двух дисбалансов, толщины диска, величины нелинейности упругой опоры на устойчивость вертикального жесткого гироскопического ротора.

На рисунке 1 представлена геометрическая схема ротора. Вал с длиной  и жесткостью  установлен вертикально с помощью нижней шарнирной и отстоящей от нее на расстояние  верхней упругой опоры. На свободном конце вала закреплен диск, имеющий массу , полярный момент инерции  и поперечный момент инерции , одинаковый для любого направления. Скорость вращения вала  настолько большая, что ротор можно рассматривать как гироскоп, неподвижной точкой которого является нижняя опора вала. Положение геометрического центра диска определяется координатами , , а положение вала и в целом ротора в пространстве углами ,  и углом поворота . Далее обозначим координаты центра масс диска  через  и . Положение оси симметрии диска  определяется углами , и . Предполагаем также, что линейный эксцентриситет  лежит на оси  и отстает от плоскости углового эксцентриситета  на угол . Ограничимся малыми отклонениями оси ротора, поэтому будем учитывать в вычислениях члены линейные относительно малых величин.

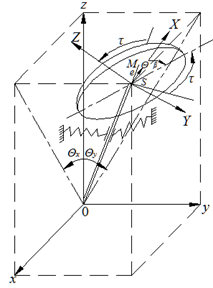
Рис.1. Геометрия ротора

Учитывая изложенное выше проекции угловой скорости на координатных

осях подвижной системы запишем в виде

, (1)

а кинетическую энергию системы,

,

учитывая, что  и (1), получим в форме

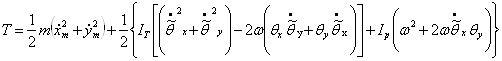, (2)

где

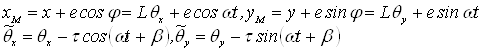 (3)

Потенциальная энергия системы имеет вид

, (4)

где  – коэффициент жесткости упругой опоры,  – коэффициент в нелинейном члене упругой силы.

Моменты внешних сил имеют вид

 (5)

где – вес диска.

Учтем диссипативныe силы, заданные в виде

 (6)

где –коэффициент внешнего демпфирования.

Уравнения Лагранжа второго рода для роторной системы представим в виде

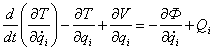 (7)

Здесь – обобщенные координаты;  – обобщенные силы.

Подставляя выражения (2) – (6) в (7),введя следующие безразмерные параметры

 (8)

и используя обозначения выражений амплитуды

   (9)

и начальной фазы

 (10)

вынуждающего момента выражая с одними гармоническими функциями можно придать уравнениям движения компактный вид

 (11)

  (12)

где  - условная толщина диска.

Таким образом, оказывается, что состояние стационарного движения рассматриваемого ротора описывается системой дифференциальных уравнений (4) и (5) типа Дуффинга.

Аппроксимация решений уравнений (11) и (12) в случае основного резонанса простой гармоникой с частотой колебаний, равной частоте возмущающего момента удовлетворяет

 (13)

 (14)

Для решения вопроса об устойчивости рассмотрим малые отклонения и от периодических равновесных состояний в уравнениях (11), (12) заменяя величиныи на и .Здесь и -периодические решения уравнений (11)и(12),устойчивость которых подлежать исследованию. Далее, пренебрегая степенями и выше первой и получаем линейные уравнения относительно вариацийи  [5,6]

 , (15)

. (16)

Характер поведения величин и во времени определяет соответствующих решений и : если все решения иуравнений (15) и (16) при ,то решения и  по определению устойчивы; если величины  и неограниченно растет при ,то решения  по определению неустойчивы.

Используя преобразования

 и (17)

и заменяя величиныи  их разложениями (13) и (14), приводим уравнения (15) и (16) к уравнениям типа Хилла:

, (18), (19)

где

;

;

- (20)

некоторые функции от аргументов . Согласно теории Флоке, частные решения уравнений (18) и(19) ищем в виде

, (21)

, (22)

где- характеристический показатель (действительный или мнимый). Из равенств (17), (21) и (22) непосредственно видно, что условия, определяющие устойчивость решенийи имеют вид

Re<0, (23)

а на границе между областями устойчивости и неустойчивости

Re=0. (24)

Поскольку характеристический показатель может быть или действительным, или чисто мнимым, то условие (23) эквивалентно следующему:

>0 и > (25)

Подставляя решения (21) и (22) в уравнения (18) и (19) и применяя метод гармонического баланса, т. е. приравнивая друг другу коэффициенты при одинаковых частотах получаем систему линейных однородных уравнений, которая должна удовлетворяться при любых нетривиальных значениях величин  и . Поэтому характеристический определитель, составленный из коэффициентов, должен обратиться в нуль. Этот определитель зависит от величины .Таким образом,

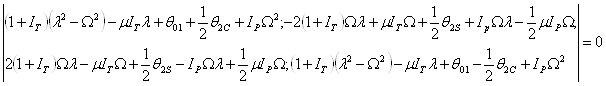(26)

Из условий (23) – (25)следует, что [5, 6]:

 на границе областью устойчивости и областью неустойчивости

и

>0 в области устойчивости.

Раскрывая определитель (26) и учитывая выражения (24), можно получить соотношение, определяющее границу любой из областей неустойчивости на резонансных кривых:

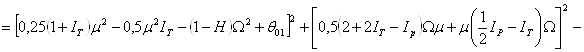
 (27)

При этом области устойчивости характеризуются неравенством

>0 (28)

Уравнение (27) решалось на компьютере численным методом в системе символьных вычислений «Maple 11» для следующих параметров ротора:

  .

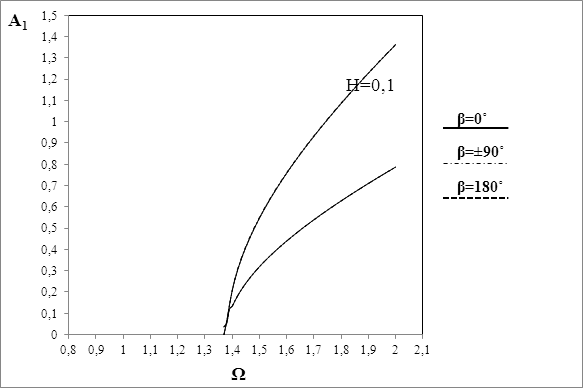
Рис. 2. Влияние угла между ориентациями дисбалансов на границы области неустойчивости основного резонанса. Случай тонкого диска

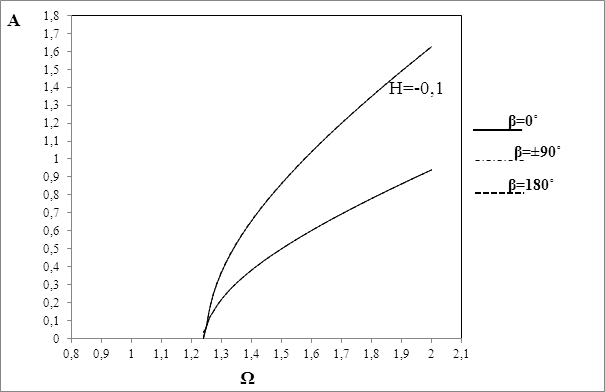
Рис. 3. Влияние угла между ориентациями дисбалансов на границы области неустойчивости основного резонанса. Случай толстого диска

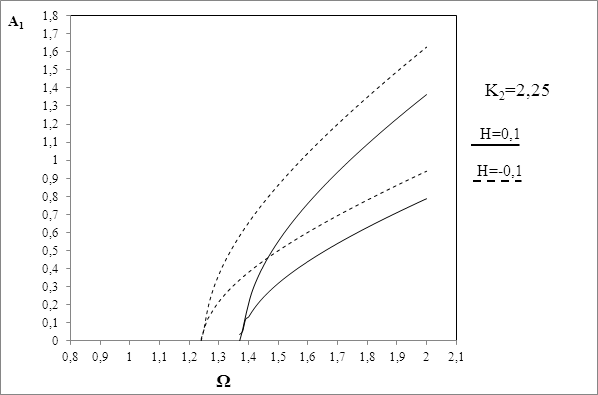
Рис. 4. Влияние толщины диска на границы области неустойчивости основного резонанса

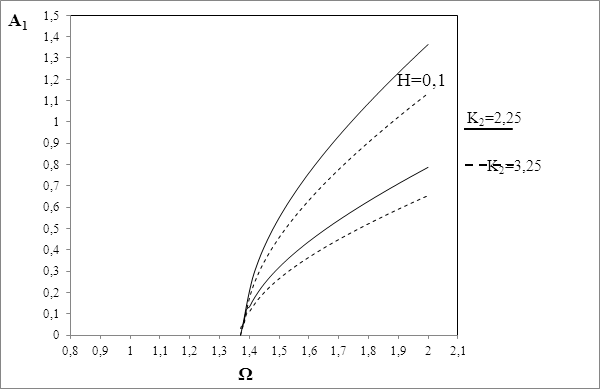
Рис. 5. Влияние величины нелинейности на границы области неустойчивости основного резонанса. Случай тонкого диска

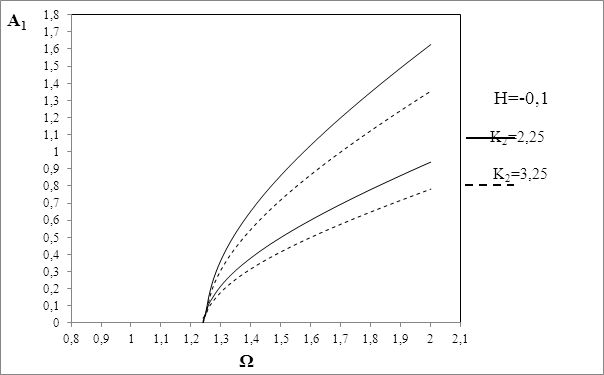
Рис. 6. Влияние величины нелинейности на границы области неустойчивости основного резонанса. Случай толстого диска

Графики на рис.2 и 3 и расчеты по формуле (27) показывают слабую зависимость границы области неустойчивости от угла между ориентациями

дисбалансов. Из рис.4 было видно влияние толщины диска на положение иширину области неустойчивости. При одинаковой скорости вращения ширина области неустойчивости для тонкого диска меньше, чем анлогичный параметр для толстого диска. Графики на рис.5 и 6 показывают, что с ростом величины нелинейности области неустойчивости смещаются вниз и их ширина уменьшается. Как видно из выражения (27), параметры конструкции нашли свое отражение в выражении области неустойчивости ротора. Следовательно варируя ими, можно подобрать оптимальные режимы работы машины,исключающие резонансные явления.

Таким образом,результаты исследований влияния толщины, дисбаланса массы и перекоса диска, взаймной их ориентаций,нелинейного параметра упругой опоры, а также вязкого трения на главные резонансные колебания и их устойчивость позволяют создавать методы балансировки, определить безопасную рабочую область скоростей, находить эффективные параметры для надежной работы машины.

Список литературы:

1.            Бенсон. Установившиеся колебания консольного ротора с перекосом и дисбалансом диска // Конструирование и технология машиностроения. -1983.-Т.105, № 4. – С. 35—40.

2.             Искаков Ж. Установившиеся колебания двух опорного консольного ротора с перекосом и дисбалансом диска. // Доклады Академии наук Республики Казахстан. – 2008. - № 1. – С. 18 – 25.

3.             Тулешов А. К., Искаков Ж., Калыбаева А. К. Динамика вертикального гироскопического ротора с перекосом диска и дисбалансом массы. // Вестник КазНПУ имени Абая. Серия физико – математических наук. – Алматы, 2010. - № 3 (31). - С. 184 – 194.

4.             Төлешов А.Қ., Искаков Ж., Калыбаева А.Қ. Массасының дисбалансы мен дискісінің еңкіштігі бар бейсимметриялық ротордың орныққан тербелістері. – // Әл – Фараби атындағы Қазақ Ұлттық Университетінің Хабаршысы. - Алматы, 2010. - № 4(67). – Б. 264 – 271.

5.             Хаяси Т. Нелинейные колебания в физических системах. – М.: Мир, 1968.

6.             Szemplinska-Stupnicka W.Higher harmonic oscillations in heteronymous nonlinear systems with one degree of freedom //Internal.J.Nonlinear Mech.-1968.-Vol. 3,N 1.-P.17-30.