Статья опубликована в рамках: II Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 16 апреля 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Часть I, Часть II, Часть III, Часть IV, Часть V
дипломов
МОДЕЛИРОВАНИЕ НАГРЕВА В ПРОЦЕССЕ ПРЕССОВАНИЯ ЛОНЖЕРОНА ЛОПАСТИ И СИНТЕЗ МОДАЛЬНОГО РЕГУЛЯТОРА
Рахматуллина Лена Рифатовна
студентка 3 курса, кафедра промышленной автоматики филиала ФГБОУ ВПО УГАТУ в г. Кумертау
E-mail: grachevaln@bk.ru
Епифанова Наталья Анатольевна
студентка 3 курса, кафедра промышленной автоматики филиала ФГБОУ ВПО УГАТУ в г. Кумертау
Грачева Любовь Николаевна
научный руководитель, канд. тех. наук, доцент, кафедра промышленной автоматики филиала ФГБОУ ВПО УГАТУ в г. Кумертау
E-mail: grachevaln@bk.ru
При решении задач синтеза систем управления на практике довольно часто можно столкнуться с задачей синтеза САУ объектов с запаздыванием. Одним из таких объектов является нагрев пресс-формы и формируемого лонжерона лопасти вертолета из стеклопластика в процессе прессования.
Целью данной работы является сравнения двух математических моделей рассматриваемого объекта и синтез модального регулятора на их основе.
Передаточная функция этого объекта на этапе предварительного нагрева и нагревания имеет вид [1, 2]:
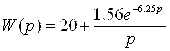 (1).
(1).
Эквивалентное звено запаздывание учитывает апериодическим звеном первого порядка [3]
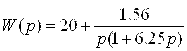 (2).
(2).
Первая задача работы состоит в том, чтобы определить степень близости передаточных функций (1) и (2). Построенные в одних осях графики переходного процесса для систем (1) и (2 ) представлены на рис. 1.
Из рис. 1 видно, что модели близки во временном интервале 130-200 мин. и температуре 200—3000С, а на других интервалах расходятся. Численные расчеты показали, что максимальное отклонение моделей друг от друга достигается в рабочем диапазоне температур при 57—600С и составляет 14,04 %, а среднее отклонение близко к 5 %. Таким образом, модели (1) и (2) достаточно близки.
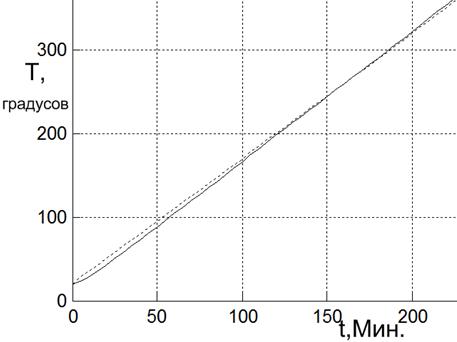
Рисунок 1. Сопоставление систем (1 — сплошная линия)
и (2 — пунктирная линия)
Вторая задача данной работы состоит в том, чтобы сравнить результаты синтеза модального регулятора для систем (1) и (2).
Модальный регулятор определяется на основе структурной схемы САР, представленной на рис. 2. Здесь объект задан уравнениями в пространстве состояний — матрицы А, В, С, D, а регулятор матрицей обратных связей — К [3].
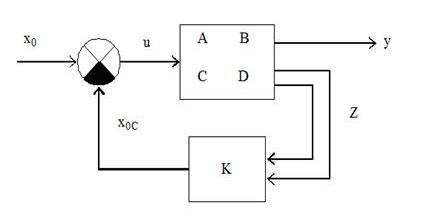
Рисунок 2. Структурная схема САР с Модальным регулятором
Выполним анализ объекта, заданного формулой (1). Такая система находится на границе устойчивости и нуждается в коррекции, так как корни системы :
р1 = 0, р2 = –0.1600
Получим модель объекта в пространстве состояний в виде [3]:
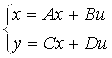
где:

Исследование системы на управляемость показало, что она управляема, так как ранг матрицы управляемости максимальный:
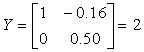
Исследование системы на наблюдаемость показало, что система наблюдаема, так как ранг матрицы наблюдаемости максимален и равен 2:

Синтез системы с модальным регулятором выполняется по заданному расположению корней. Так как один из корней системы равен 0, то его необходимо сдвинуть в отрицательную полуплоскость для того, чтобы обеспечить устойчивость синтезируемой системы, например:
p=[–0.16 ;–0.16].
Тогда коэффициенты обратных связей примут вид: ![]()
Выполним аналогичные действия для формулы (2). Для этого представим звено с запаздываением следующим образом:
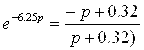
Сиcтема, заданная формулой (2), является направляемой и наблюдаемой с корнями: р=[0; –0,32].
Выполним сиснтез модального регулятора для системы (2) при таком же расположении корней, как и для системы (1). Сравнение результатов моделирования систем (1) и (2) после коррекции с корнями [–0,16 –0,16] представлено на рис. 3.
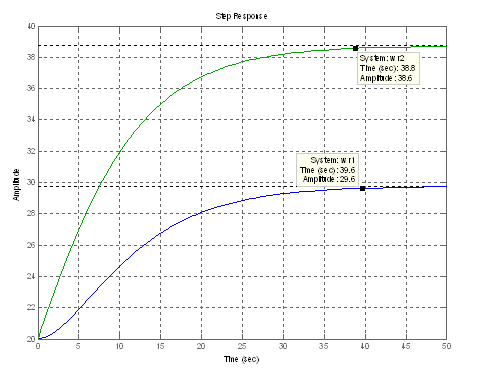
Рисунок 3. Результаты моделирования систем после модального регулирования по расположению корней [–0.16 –0.16]
Приняв для синтеза модального регулятора расположение корней p=[–0.32 –0.32], получим графики переходного процесса для систем (1) и (2) — рис. 4.
Таким образом, несмотря на достаточную близость математических моделей (1) и (2) результаты синтеза модального регулятора значительно различаются, поэтому для корректного синтеза модального регулятора необходимо оценить степень адекватности моделей (1) и (2) реальному объекту.
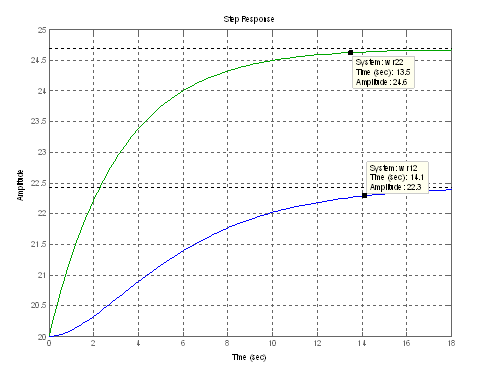
Рисунок 4. Результаты моделирования систем после модального регулирования по расположению корней [–0.32 –0.32]
Список литературы:
- Грачева Л. Н., Полякова Л. Ю. Автоматизация процессов изготовления деталей из полимерных композитных материалов для авиационной техники: монография. / Оренбург: ИПК ГОУ ОГУ, 2009. — 108 с.
- Грачева Л. Н., Даутов А. И., Полякова Л. Ю., Тюков Н. И. Автоматизация процесса прессования лонжерона лопасти ииз полимерных композиционных материалов: монография. / Уфа: Гилем, 2009. — 144 с.
- Макаров И. М., Менский Б .М. Линейные автоматические системы: учебное пособие для вузов / М.: Машиностроение, 1977. — 464 с.
- Савин М. М., Елсуков В. С., Пятина О. Н. Теория автоматического управления: учебное пособие./ Ростов н/Д: Феникс, 2007. — 469 с.
дипломов


Оставить комментарий