Статья опубликована в рамках: XXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЕСТЕСТВЕННЫЕ НАУКИ» (Россия, г. Новосибирск, 20 января 2015 г.)
Наука: Физика
Секция: Астрономия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ИЗУЧЕНИЕ СОЛНЕЧНЫХ ПЯТЕН И СОЛНЦА ПРИ ИХ ПОМОЩИ
Борисов Святослав Борисович
студент 2 курса, физический факультет МГУ им. М.В. Ломоносова, РФ, г. Москва
E -mail: sb.borisov@physics.msu.ru
Сегодня исследования Солнца становятся все более актуальными. Одна из причин этого — развитие космической отрасли: необходимо предсказывать поведение Солнца, чтобы вовремя защищать спутники, планетоходы и, самое главное, космонавтов от солнечной радиации. Еще одна причина — пагубное влияние солнечных вспышек на работу электросетей и приборов на Земле. Чтобы сеть не вышла из строя, необходимо ее вовремя отключить, для чего нужно заранее знать о появлении вспышки. Развитие сельского хозяйства также тесно связано с солнечной активностью.
Целью настоящей работы является исследование дифференциального вращения Солнца. Природа этого явления до сих пор до конца неясна. Однако есть веские основания предполагать, что солнечная активность коррелирует со средней величиной скорости вращения. Поэтому второй целью работы является оценка активности Солнца в нынешнем солнечном цикле, основанная на данных статьи [2].
Часть 1.Исследование дифференциального вращения Солнца
Дифференциальное вращение Солнца — явление, суть которого заключается в том, что на разных гелиографических широтах (далее — широтах) звезда вращается с разной угловой скоростью, то есть нетвердотельно. Существует несколько работ (в том числе [2], [4]), посвященных изучению дифференциального вращения, в которых авторы искали связь между угловой скоростью и широтой. Оказалось, что эта связь меняется от цикла к циклу. Данная работа нацелена на выявление зависимости в нынешнем 24-ом цикле.
Для изучения данной проблемы использовались фотографии размером 512×512 пикселей, выполненные спутником SDO (Solar Dynamics Observatory) в период с декабря 2013 г. по июль 2014 г., а также несколько фотографий, сделанных в июле 2014 г. автором статьи.
Для вычисления угловой скорости вращения были использованы наблюдения за солнечными пятнами. Целесообразность этого метода состоит в том, что, во-первых, заметить пятна на поверхности Солнца намного проще, чем другие образования, и, во-вторых, в течение своей жизни пятно практически не меняет своей широты. Для вычислений мы принимали во внимание только те пятна, которые наблюдались не менее 3 дней. Угловая скорость пятна рассчитывалась по формуле ![]() (1), где
(1), где ![]() — изменение долготы за время
— изменение долготы за время ![]() . Для удобства были использованы фотографии, сделанные с интервалом в 1 сутки с точностью до минуты. Таким образом, задача сводилась к вычислению широты пятна и изменения его долготы. Это делалось следующим образом: при помощи программы «Iris» рассчитывались координаты (x, y) центра пятна на фотографиях изо дня в день. В ходе работы была выведена формула, связывающая изменение координат (x, y) с изменением долготы:
. Для удобства были использованы фотографии, сделанные с интервалом в 1 сутки с точностью до минуты. Таким образом, задача сводилась к вычислению широты пятна и изменения его долготы. Это делалось следующим образом: при помощи программы «Iris» рассчитывались координаты (x, y) центра пятна на фотографиях изо дня в день. В ходе работы была выведена формула, связывающая изменение координат (x, y) с изменением долготы:
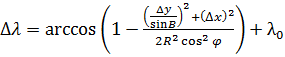 , (2)
, (2)
где: ![]() и
и ![]() — изменение координат,
— изменение координат,
![]() — широта,
— широта,
![]() — широта центра видимого диска (ввиду несовпадения плоскостей солнечного экватора и земной орбиты эта величина меняется с амплитудой 7,25°; значения B на каждый день бралось из таблицы эфемерид [1, c. 434]),
— широта центра видимого диска (ввиду несовпадения плоскостей солнечного экватора и земной орбиты эта величина меняется с амплитудой 7,25°; значения B на каждый день бралось из таблицы эфемерид [1, c. 434]),
R — радиус изображения Солнца на фотографии в пикселях,
![]() — добавка, равная примерно 0,986°, связанная с движением Земли по орбите. Широта рассчитывалась по следующей выведенной нами формуле:
— добавка, равная примерно 0,986°, связанная с движением Земли по орбите. Широта рассчитывалась по следующей выведенной нами формуле:
![]() , (3)
, (3)
где: ![]() — y-координата пятна в момент прохождения центрального меридиана (на изображении это вертикальная линия, проходящая через центр изображения),
— y-координата пятна в момент прохождения центрального меридиана (на изображении это вертикальная линия, проходящая через центр изображения),
256 — y-координата центра изображения. Погрешность широты связана с ошибкой определений центра пятна, которая принималась равной 1 пикселю.
На рисунке 1 — пример двух последовательных фотографий Солнца.
Для каждого пятна величина ![]() рассчитывалась несколько раз (от 2 до 7) — в каждый день наблюдений, кроме первого. Далее эта величина усреднялась, а за погрешность было взято стандартное отклонение. Описанная выше операция была выполнена для 31 пятна. Пример расчетной таблицы с промежуточными вычислениями в программе «Excel» приведен на рисунке 2.
рассчитывалась несколько раз (от 2 до 7) — в каждый день наблюдений, кроме первого. Далее эта величина усреднялась, а за погрешность было взято стандартное отклонение. Описанная выше операция была выполнена для 31 пятна. Пример расчетной таблицы с промежуточными вычислениями в программе «Excel» приведен на рисунке 2.


Рисунок 1. Две последовательные фотографии Солнца
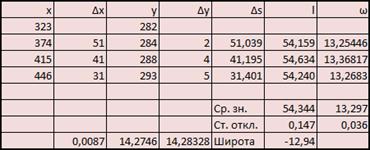
Рисунок 2. Пример расчетной таблицы в «Excel»
Для выявления зависимости между угловой скоростью вращения и широтой был применен метод наименьших квадратов (МНК). Как правило, эту зависимость аппроксимируют прямой вида ![]() (4). В таблице 1 представлены данные, для которых применялся МНК, рассчитанные на основе фотографий по выведенным нами формулам.
(4). В таблице 1 представлены данные, для которых применялся МНК, рассчитанные на основе фотографий по выведенным нами формулам.
Таблица 1.
Данные, использовавшиеся для выявления зависимости ![]()
|
|
ω, °/сут |
|
ω, °/сут |
|
ω, °/сут |
|
ω, °/сут |
|
0,05045 |
14,30 |
0,02399 |
14,33 |
0,08843 |
14,13 |
0,07069 |
14,17 |
|
0,09365 |
14,18 |
0,05014 |
14,28 |
0,02426 |
14,37 |
0,0199 |
14,31 |
|
0,04231 |
14,29 |
0,06126 |
14,23 |
0,05394 |
14,30 |
0,0179 |
14,35 |
|
0,04245 |
14,30 |
0,00727 |
14,36 |
0,06001 |
14,27 |
0,01823 |
14,34 |
|
0,05183 |
14,25 |
0,01046 |
14,37 |
0,008 |
14,42 |
0,02164 |
14,28 |
|
0,00321 |
14,36 |
0,03045 |
14,33 |
0,04677 |
14,26 |
0,06051 |
14,22 |
|
0,05968 |
14,28 |
0,04618 |
14,23 |
0,10826 |
14,11 |
0,04685 |
14,27 |
|
0,16621 |
13,90 |
0,00109 |
14,42 |
0,05489 |
14,24 |
|
|
Для МНК использовалась программа «OriginPro 9». График ![]() с проведенной аппроксимирующей линией и ее коэффициентами приведен ниже.
с проведенной аппроксимирующей линией и ее коэффициентами приведен ниже.
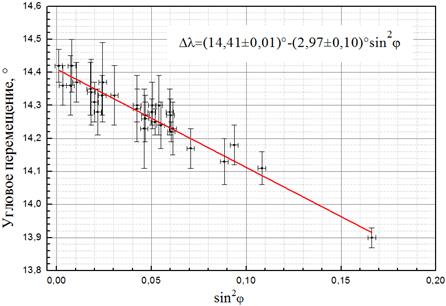
Рисунок 3. График зависимости ![]()
Таким образом, в результате обработки данных коэффициент A получился равным (14,41±0,01)°/сут., а коэффициент K -(2,97±0,10)°/сут.
Анализируя полученный результат, можно рассчитать период обращения Солнца на экваторе, приняв φ=0: ![]() . Если подставить φ=90°, то получится период обращения около полюсов — (31,47±1,17) сут., что близко к реальности (примерно 33 дня). Однако считать его таким методом нецелесообразно ввиду того, что пятна редко появляются на широтах больше 35° (в данной работе самое «высокое» пятно имело широту 24,06°).
. Если подставить φ=90°, то получится период обращения около полюсов — (31,47±1,17) сут., что близко к реальности (примерно 33 дня). Однако считать его таким методом нецелесообразно ввиду того, что пятна редко появляются на широтах больше 35° (в данной работе самое «высокое» пятно имело широту 24,06°).
Далее все пятна были разделены на две группы: северные (φ>0) и южные (φ<0). К каждой группе был применен МНК для сравнения зависимости ![]() в разных полушариях. Результат получился следующий:
в разных полушариях. Результат получился следующий:
для северных пятен:
![]() (5);
(5);
для южных пятен:
![]() (6).
(6).
Видно, что скорость в южном полушарии убывает быстрее, то есть средняя скорость здесь меньше, чем в северном. Небольшое расхождение может быть связано с тем, что не был учтен очень слабый эффект — некоторое несовпадение плоскостей солнечного экватора и земной орбиты. Также не исключено, что эта зависимость, действительно, разная для полушарий. Подобный результат представлен в статье [4, p. 10], где рассматривалось вращение в 20-ом солнечном цикле, то есть в цикле с той же полярностью, что и в нынешнем. Можно предположить, что в циклах с другой полярностью происходит наоборот — быстрее вращается южное полушарие. Выяснение этого явления — одна из дальнейших целей, которую ставит перед собой автор данной статьи.
Часть 2. Оценка активности Солнца в 24-ом цикле
Анализируя результат, полученный в первой части данной работы, можно сделать оценку пика активности Солнца в нынешнем 24-ом цикле. Показателем его активности является число Вольфа W, определяемое количеством пятен и их групп и рассчитываемое по формуле ![]() (7), где
(7), где ![]() — количество пятен,
— количество пятен, ![]() — количество групп пятен. Для оценки активности были использованы данные статьи [2], где авторы обратили внимание на такой факт: в циклы, когда активность Солнца велика, средняя экваториальная скорость меньше, чем в циклы с малой активностью. К сожалению, поскольку солнечный цикл длится примерно 11 лет, то есть срок довольно большой, данных о скорости вращения было накоплено мало — всего для 4 циклов. Нанося на график W(A) точки и применяя МНК, можно получить следующую картину (рисунок 4).
— количество групп пятен. Для оценки активности были использованы данные статьи [2], где авторы обратили внимание на такой факт: в циклы, когда активность Солнца велика, средняя экваториальная скорость меньше, чем в циклы с малой активностью. К сожалению, поскольку солнечный цикл длится примерно 11 лет, то есть срок довольно большой, данных о скорости вращения было накоплено мало — всего для 4 циклов. Нанося на график W(A) точки и применяя МНК, можно получить следующую картину (рисунок 4).

Рисунок 4. График зависимости W(A)
Полученная зависимость дает оценку числа Вольфа в пике 24-ого цикла, равную 175±18. Реальное значение, согласно данным Института Прикладной Геофизики им. Е.К. Федорова, равно 168. Видно, что оценка оказалась весьма точной. Это одно из первых подтверждений эмпирического закона, представленного в статье [2]. Таким образом, рассчитывая коэффициент А в первые годы цикла, можно предсказывать, насколько активным Солнце будет в пике этого цикла.
Часть 3.Изучение структуры солнечных пятен
Изучение структуры солнечных пятен, а именно их геометрической формы — третья цель данной работы. Одно из первых серьезных исследований геометрической формы пятна было проведено шотландским астрономом А. Уилсоном. Он обратил внимание, что при нахождении пятна близ лимба солнечного диска одна сторона полутени, которая ближе к лимбу, кажется толще другой. Это навело Уилсона на мысль, что пятно представляет собой «воронку», или «тарелку» (рисунок 5). Дальнейшие исследования Солнца подтвердили это.
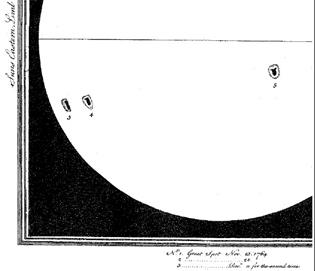
Рисунок 5. Зарисовка Солнца из работы А. Уилсона
Этот раздел нашей работы посвящен определению геометрической формы пятен. Автором работы было предложено три новых метода определения формы пятен, ни один из которых ранее не встречался в литературе. Два из них, как и все описанные ранее, требуют практически непрерывного наблюдения пятна и в данной статье не рассматриваются. Третий метод не нуждается в этом; для его применения необходимо лишь два наблюдения пятна в разных положениях. Это его серьезный «плюс», особенно при земных наблюдениях, которые зависимы от погодных условий и длительности нахождения солнца над горизонтом. «Минус» метода — предположение, что форма пятна одинакова в оба момента времени наблюдений. Именно поэтому были использованы фотографии, сделанные с небольшим временным интервалом.
Известно, что со временем видимая проекция полутени пятна меняет свой размер. Поэтому, выведя формулу связи видимой проекции p1,2 полутени («склона»), длины «склона» x, глубины пятна h, угла β между плоскостью полутени и касательной плоскостью и разностью долгот между краем полутени и центральным меридианом λ1,2, можно получить его геометрическую форму. На рисунке 6 изображена схема пятна в обоих положениях.

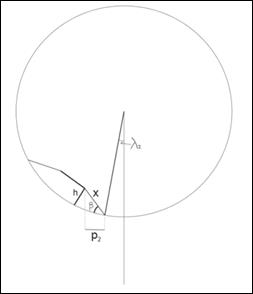
Рисунок 6. Схема пятна в обоих положениях
Выведенные нами расчетные формулы имеют следующий вид:
![]() (8)
(8)
![]() (9)
(9)
Последняя формула дает значение глубины в пикселях, то есть, если бы имелась трехмерная модель Солнца, то пятно имело бы глубину h пикселей. Для перевода данной глубины в километры ее надо умножить на ![]() , где R — радиус изображения Солнца в пикселях, Rs — радиус Солнца (696 000 км).
, где R — радиус изображения Солнца в пикселях, Rs — радиус Солнца (696 000 км).
Результаты измерений приведены в таблице 2.
Таблица 2.
Данные о глубине и угле наклона β для 14 пятен
|
№ |
Глубина h, км |
Угол наклона β, ° |
№ |
Глубина h, км |
Угол наклона β, ° |
|
1 |
620±130 |
6,6±1,0 |
8 |
1170±110 |
8,3±0,4 |
|
2 |
1620±330 |
8,4±1,1 |
9 |
830±50 |
6,3±0,2 |
|
3 |
1410±70 |
8,6±1,2 |
10 |
930±50 |
5,7±0,2 |
|
4 |
1380±60 |
9,2±1,2 |
11 |
1290±140 |
7,3±0,5 |
|
5 |
1140±40 |
6,6±1,1 |
12 |
1000±60 |
7,3±0,3 |
|
6 |
1510±240 |
4,9±0,3 |
13 |
820±100 |
6,0±0,5 |
|
7 |
1470±230 |
9,6±0,6 |
14 |
1070±130 |
6,9±0,7 |
Средняя глубина пятна получилась равна 1160 км. Этот результат близок к тем, что были получены в статьях [3, p. 109], [5, p. 224] и [6, p. 16]. Средний угол наклона 7,3°, что говорит о том, что пятна представляют собой весьма плоские «блюдца».
В ходе работы было проверено, зависит ли глубина пятна h от его площади S. Площадь рассчитывалась в программе «Heliograph» в м.д.п. — миллионных долях полусферы. На рисунке 7 на график h(S) нанесены точки для 14 пятен.
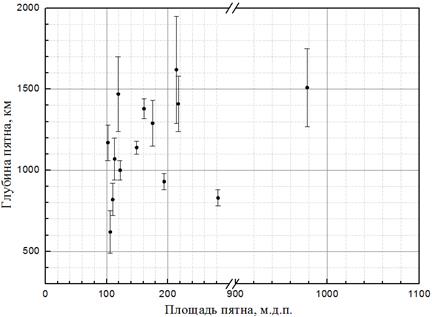
Рисунок 7. График h(S)
Видно, что глубина пятен не коррелирует с их площадью. Из того факта, что напряженность магнитного поля в пятне связана с его площадью, следует вывод, что связи напряженности с глубиной, скорее всего, нет.
В ходе выполнения работы был получен интересный результат: отношение площади тени пятна к полной площади пятна почти всегда одинаково. Среднее значение этого отношения равно 0,168±0,014 (отн. погрешность 8,33 %). Данные о площадях тени и полутени приведены в табл. 3.
Таблица 3.
Данные о площадях полутени и тени
|
№ |
Площадь тени, м.д.п. |
Площадь пятна, м.д.п. |
№ |
Площадь тени, м.д.п. |
Площадь пятна, м.д.п. |
|
|
1 |
19 |
106 |
8 |
18 |
102 |
|
|
2 |
35 |
214 |
9 |
45 |
282 |
|
|
3 |
37 |
217 |
10 |
29 |
194 |
|
|
4 |
28 |
161 |
11 |
25 |
175 |
|
|
5 |
24 |
149 |
12 |
20 |
122 |
|
|
6 |
205 |
978 |
13 |
16 |
110 |
|
|
7 |
22 |
119 |
14 |
19 |
113 |
|
Вывод
Результатом работы стало получение зависимости угловой скорости вращения Солнца от широты в нынешнем 24-ом цикле. По результатам исследования дифференциального вращения была сделана достаточно точная оценка активности Солнца в 24-ом цикле. Рассчитаны геометрические параметры 14 солнечных пятен и выявлены новые интересные факты.
Список литературы:
1.Куликовский П.Г. Справочник любителя астрономии. М.: Эдиториал УРСС, 2002. — С. 434.
2.Kambry M.A., Nishikawa J. Solar differential rotation derived from sunspot observations // Solar Physics. — 1990. — № 126 — P. 89—100.
3.Prokakis Th. The depth of sunspots // Solar Physics. — 1974. — № 35 — P. 105—110.
4.Schröter E.H., Wöhl H. Differential rotation, meridional and random motions of the solar Ca+ network // Solar Physics. — 1975. — № 42 — P. 3—16.
5.Suzuki Y. On the Wilson effect of the sunspots // PASJ — 1967. — № 2. — Vol. 19 — P. 220—228.
6.Watson F., Fletcher L., Dalla S., Marshall S. Modeling the longitudinal asymmetry in sunspots emergence — the role of the Wilson depression // Solar Physics. — 2009. — № 260 — P. 5—19.
отправлен участнику


Комментарии (7)
Оставить комментарий