РАЗВИТИЕ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА НА УРОКАХ МАТЕМАТИКИ ПОСРЕДСТВОМ ИСПОЛЬЗОВАНИЯ ИСТОРИЧЕСКОГО МАТЕРИАЛА

Рудобелец Юлия Сергеевна

студент 5 курса, кафедра математики, информатики и методики преподавания КФ НГПУ, г. Куйбышев, Новосибирской области

Е-mail: 

Александрова Зоя Алексеевна

научный руководитель, старший преподаватель КФ НГПУ, г. Куйбышев, Новосибирской области

Эффективность обучения, в частности обучения математике, во многом зависит от того, насколько учащиеся проявляют интерес к изучаемому материалу. Поэтому проблема развития познавательного интереса учащихся актуальна как для исследователей, так и для практиков. Познавательный интерес взаимосвязан со многими сторонами учебного процесса.

В педагогической практике познавательный интерес рассматривают часто как средство активизации познавательной деятельности ученика, как эффективный инструмент в работе учителя. Данный «инструмент» позволяет ему сделать процесс обучения привлекательным, выделить в обучении те пункты, которые смогут привлечь к себе непроизвольное внимание учеников, заставят активизировать мышление, волноваться и переживать, увлеченно работать над учебной задачей. Но опыт многих педагогов и учителей показывает, что уроки математики школьники относят к числу нелюбимых предметов. Деятельность учащихся на этих уроках у многих учителей носит однообразный воспроизводящий характер. Большая часть времени на уроках отведена на выполнение тренировочных заданий.На основе специальных исследований психологов и педагогов видно, что к шести годам у дошкольников формируется внутренняя потребность занять более взрослое положение. Ее центром становится желание учиться. Обычно все первоклассники хотят учиться, и не просто учиться, а только на одни пятёрки. Однако в педагогической практике можно наблюдать падение от класса к классу у некоторых школьников интереса к учебной деятельности.

Встает проблема, каким же образом организовать обучение так, чтобы увлечь ребенка процессом познания, пробудить стремление к самостоятельному овладению знаниями и умениями, как к чему-то для него ценному, привлекательному, то есть, как развить познавательный интерес, как к «интересному», так и к «скучному» предмету?

В данной статье рассмотрим развитие познавательного интереса к уроку математики на основе использования различным методических приёмов и заданий с историческим материалом.

Рассмотрим различные подходы к определению понятия «познавательный интерес», а также стадии и уровни его развития.

Интерес (от латинского «имеет значение, важно») — реальная причина действий, ощущаемая учеником как особо важная.

Интерес — это форма проявления познавательных потребностей, что выражается в стремлении к познанию объекта или явления, овладении определённым видом деятельности.

Л.С. Выготский называл интерес как бы естественным двигателем детского поведения. «Он является выражением инстинктивного стремления, указанием на то, что деятельность ребёнка совпадает с его органическими потребностями» [2, с. 54]. Вот почему Л.С. Выготский считал основным правилом построения всей образовательно-воспитательной системы точный учёт детских интересов. Важным также является то, насколько интерес направлен по линии самого изучаемого предмета, а не связан с посторонним для него влиянием наград, наказаний, страха, желания угодить и т. п.

Н.Г. Морозова считает, что «интерес можно определить как эмоционально-познавательное отношение к предмету или к непосредственно мотивированной деятельности, отношение, переходящее при благоприятных условиях в эмоционально-познавательную направленность личности» [4, с. 22].

Применительно к учебной деятельности А.К. Маркова [3] выделяет следующие виды интереса к учению:

1.  Глобальный, недифференцированный, т. е. широкий учебный интерес.

2.  Интерес к постановке целей, задач, их реализации, т.е. планирующий учебный интерес.

3.  Интерес к результатам учения, т. е. результативный учебный интерес.

4.  Интерес к содержанию предмета, к процессу его усвоения, т. е. процессуально-содержательный.

5.  Более глубокий интерес к процессу и к способам, приёмам его осуществления, т. е. учебно-познавательный интерес.

6.  Стремление к преобразованию и совершенствованию своей учебной работы, т. е. преобразующий интерес.

Таким образом, познавательный интерес является одним из видов интереса к учению. Г.И. Щукина даёт такое определение познавательного интереса: «Познавательный интерес выступает перед нами как избирательная направленность личности, обращённая к области познания, к её предметной стороне и к самому процессу овладения знаниями» [6, с. 67].

По основанию активности и самостоятельности учащихся, стремлению к преодолению трудностей Г.И. Щукина [7] выделяет уровни проявления становления интереса к учению (Таблица 1):

Таблица 1.

Уровни проявления становления интереса к учению

Познавательный интерес как одна из разновидностей интереса к учению может проявляться на любом из этих уровней.

С этой классификацией связаны уровни сформированности собственно познавательного интереса по М.В. Матюхиной (Таблица 2):

Таблица 2.

Уровни сформированности познавательного интереса

Подобные уровни выделяет Г.И. Щукина [7].

По основанию тесноты связи с эмоциональной стороной личности

Н.Г. Морозова [4]выделяет следующие виды познавательного интереса:

·эпизодическое переживание;

·эмоционально-познавательное отношение к предмету;

·стойкая эмоционально-познавательная направленность личности на определённую область знания или деятельности.

В.В. Давыдов, Д.Б. Эльконин, В.В. Репкин выделяют виды познавательного интереса по основанию обращённости ученика на отдельные стороны учебной деятельности:

·познавательный интерес, обращённый на знания как результат учения;

·познавательный интерес, обращённый на способ добывания знаний.

Познавательный интерес по-разному проявляется в разных сферах деятельности.

Исследователями были выделены проявления, параметры и критерии познавательного интереса.

1.  Проявление интеллектуальной активности (вопросы к учителю, стремление по собственному побуждению участвовать в деятельности, в обсуждении вопросов на уроке, активное оперирование приобретённым багажом знаний и умений);

2.  Эмоциональное проявление (общий положительный настрой, интеллектуальная радость);

3.  Волевые проявления (сосредоточенность внимания и слабая отвлекаемость, поведение ученика при затруднениях, стремление к завершению учебных действий, реакция на звонок с урока);

4.  Внеурочные проявления (поведение на перемене, самостоятельные вопросы и суждения, беседы и спор между учащимися, добровольное взятие дополнительной и самостоятельной работы) (Г.И. Щукина [6], Н.Г. Морозова [4]).

Исследования А.К. Марковой [3] показали, что становлению и развитию познавательного интереса способствуют такие условия:

·выделение в содержании общих принципов и закономерностей, включение системы задач;

·активная деятельность школьников по преобразованию исходных вопросов и заданий для их решения;

·оценка учителем не только результата, но и способов учебной работы школьника, а также вовлечение в процесс оценивания самих школьников;

·выполнение детьми активных действий по анализу своей мотивационной сферы. К ним можно добавить также такие условия, как новизна материала, его эмоциональная окрашенность, коллективные формы организации различных видов деятельности, игровые задания, предоставление школьникам возможности выбора и др.

Таким образом, на развитие познавательного интереса влияют следующие условия и факторы:

1.  содержание учебного материала;

2.  активная и поисковая мыслительная деятельность детей;

3.  организация учебного процесса на оптимальном уровне развития учащихся;

4.  эмоциональная атмосфера обучения;

5.  оптимальное сочетание различных методических приёмов обучения.

Существует множество методических приёмов, активизирующих деятельность учащихся. Мы рассмотрим следующие приёмы, активизирующие деятельность учащихся на этапе восприятия и способствующие пробуждению интереса к изучаемому материалу: приём новизны, приём семантизации, создание проблемной ситуации.

Приём новизны предполагает включение в содержание учебного материала интересных сведений, фактов, исторических данных. Например, при изучении темы «Натуральные числа» в 5 классе ученикам можно дать следующие задания, некоторые из них требуют определённой подготовки.

1 задание

Существует большое количество определений понятию «число». О числах первый начал рассуждать Пифагор. Пифагору принадлежит высказывание «Всё прекрасно благодаря числу». По его учению число 2 означало гармонию, 5 — цвет, 6 —холод, 7 — разум, здоровье, 8 —любовь и дружбу. А число 10 называли «священной четверицей», так как 10 = 1 + 2 + 3 + 4. Оно считалось священным числом и олицетворяло всю Вселенную.

1.  Приготовьте рассказ посвящённый данным числам и их символическим значениям.

2 задание

Для выполнения данного задания потребуется 9 камушек для каждого ученика.

В древние времена, когда человек хотел показать, сколькими животными он владел, он клал в большой мешок столько камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и произошло слово «калькулятор», «калькулюс» по латински означает «камень».

1.  Покажите, отложив в сторону камешки, сколько домашних животных у вас дома?

2.  Объясните, почему именно столько камушек вы отложили?

3 задание

Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.

1.  Переведите на язык древних людей числа: 0,1,5,10,15,17,20.

2.  Какие из этих чисел являются натуральными?

4 задание

Для выполнения данного задания потребуется по 3 верёвочки разного цвета (красного, жёлтого и зелёного) для каждого учащегося (количество верёвочек по усмотрению учителя).

Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета (Рисунок 1). Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочканашнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.

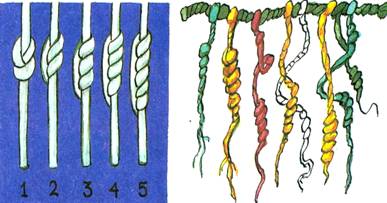
Рисунок 1.

Пусть первая верёвочка красного цвета означает сотни, вторая жёлтого цвета —десятки, и третья зелёного цвета — единицы.

1.  Завяжите на своих верёвочках числа: 1,13,99,100,123,105…

2.  Скажите, сколько в каждом числе сотен, десятков и единиц.

5 задание

Для выполнения данного задания потребуются таблички из пластилина и специально приготовленные палочки.

Народы (вавилоняне, ассирийцы, шумеры), жившие в Междуречье Тигра и Евфрата в период от II тысячелетия до н. э. до начала нашей эры, сначала обозначали числа с помощью кругов и полукругов различной величины, но затем стали использовать только два клинописных знака — прямой клин q (1) и лежащий клинt (10). Эти народы использовали шестидесятеричную систему счисления, например число 23 изображали так:ttqqqЧисло 60 снова обозначалось знаком q, например число 92 записывали так: qtttqq

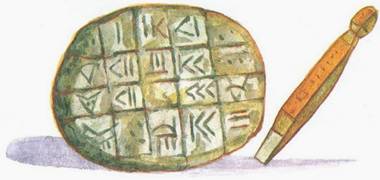
Рисунок 2.

1.  Изобразите на своих табличках числа: 6, 11, 45,58,60,64,95

2.  Скажите, сколько в каждом числе десятков и единиц.

6 задание

После счета по зарубкам люди изобрели особые символы, названные цифрами. Они стали применяться для обозначения различных количеств каких-либо предметов. Разные цивилизации создавали свои собственные цифры.

Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, …: (Рисунок 3).

Рисунок 3.

Длятого чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один— для ста, четыре — для десяти и пять иероглифов для единицы: (Рисунок 4).

Рисунок 4.

Этого одного примера достаточно, чтобы научиться записывать числа так, как их изображали древние египтяне. Это система очень проста и примитивна.

1.  Запишите иероглифами числа:6, 35, 103, 450, 5321, 26, 138.

2.  Скажите, сколько в каждом числе единиц, десятков, сотен, тысяч и т. д.

В основе приёма семантизации лежит возбуждение интереса благодаря раскрытию смыслового значения слова.

«Линия» происходит от латинского слова «линеа» — льняная (имеется в виду льняная нить).

От этого же корня происходит наше слово линолеум, первоначально означавшее льняное полотно.

Ромб происходит от латинского слова «ромбус», означающего бубен.

Мы привыкли к тому, что бубен имеет круглую форму, но раньше бубны имели форму квадрата или ромба, о чем свидетельствуют изображения «бубен» на игральных картах.

Трапеция происходит от латинского слова «трапезиум»—столик.

От этого же слова происходит наше слово «трапеза», означающее стол.

Слово «диагональ»происходит от греческого «диа», что означает «через» и « гония»— угол, т. е.рассекающая углы, проходящая через углы.

Цилиндр происходит от латинского слова «цилиндрус», означающего «валик»,«каток».

Точка— (лат. «пункт» — пунктир; «пунктум» — укол, медицинский термин «пункция»— прокол).

Прием создания проблемной ситуации позволяетне только сформировать у учащихся необходимую систему знаний, умений и навыков, достигать высокого уровня развития школьников, но и позволяет сформировать особый стиль умственной деятельности, исследовательскую активность и самостоятельность учащихся.

Мы можем предложить следующие задания на логическое мышление и поисковую деятельность:

6 класс «Деление необыкновенных дробей»

1 задание

В этом ряду есть «лишняя» дробь. Найдите её и назовите.

2 задание

Найдите ошибку и охарактеризуйте её. Какой это закон умножения? Какие ещё законы вы знаете?

Психология трудами многих выдающихся учёных (А.А. Леонтьева, С.Л. Рубинштейна, А.А. Матюшкина и др.) неоспоримо доказала, что ученик на уроке должен ставить и решать проблемы, причем непременно в диалоге с учителем. Благодаря диалогу с урока уходит пассивность, учащиеся с удовольствием думают и выражают свои мысли.

Таким образом, можно сделать выводы, что познавательный интерес к математике у школьников необходимо формировать и развивать. Помочь в этом может систематическое использование различных методологических приёмов с применением исторического материала по соответствующей теме. Знания школьников необходимо обогащать новой и интересной информацией, которая будет вызывать у них положительные эмоции и интерес к изучаемому материалу и к предмету.

Список литературы:

1.Бабанский Ю.К. Методы обучения в современной общеобразовательной школе / Ю.К. Бабанский. — М.: Просвещение, 1985. — 208 с.

2.Выготский Л.С. Педагогическая психология / Л.С. Выгодский. — М.: Просвещение, 1996. — 84 с.

3.Маркова А.К. Формирование мотивации учения / А.К. Маркова, Т.А. Матис, А.Б. Орлов. — М.: Просвещение, 1990 г. — 212 с.

4.Морозова Н.Г. Учителю о познавательном интересе / Н.Г. Морозова//Педагогика и психология. — 1979. — № 2. —с. 21—24.

5.Щукина Г.И. Активизация познавательной деятельности учащихся в учебном процессе / Г.И. Щукина. — М.: Просвещение, 1979. — 342 с.

6.Щукина Г.И. Актуальные вопросы формирования интереса в обучении / Г.И. Щукина.— М.: Просвещение, 1984. — 176 с.

7.Щукина Г.И. Педагогические проблемы формирования познавательных интересов учащихся / Г.И. Щукина. — М.: Педагогика, 1998 г. — 208 с.