РЕШЕНИЕ  ЗАДАЧ  С  ПОМОЩЬЮ  «КРУГОВ  ЭЙЛЕРА»

Рыбина  Ангелина

Класс  5  «Д»,  МОУ  «СОШ  №  59  с  УИП»,  РФ,  г.  Саратов

Багаева  Ирина  Викторовна

научный  руководитель,  педагог  высшей  категории,  преподаватель  математики,  МОУ  «СОШ  №  59  с  УИП»,  РФ,  г.  Саратов

«…  круги  очень  подходят  для  того,  чтобы  облегчить  наши  размышления»

Леонард  Эйлер

Нет  ученого,  имя  которого  упоминалось  бы  в  учебной  математической  литературе  столь  же  часто,  как  имя  Эйлера.  Даже  в  средней  школе  логарифмы  и  тригонометрию  изучают  до  сих  пор  в  значительной  степени  «по  Эйлеру».

В  1741  году  Эйлер  пишет  «Письма  о  разных  физических  и  философических  материях,  написанные  к  некоторой  немецкой  принцессе...»,  где  появились  впервые  «круги  Эйлера».  Эйлер  писал  тогда,  что  «круги  очень  подходят  для  того,  чтобы  облегчить  наши  размышления». 

При  решении  целого  ряда  задач  Леонард  Эйлер  использовал  идею  изображения  множеств  с  помощью  кругов  и  они  получили  название  «круги  Эйлера». 

С  помощью  этих  кругов  Эйлер  изобразил  и  множество  всех  действительных  чисел: 

·     N  —  множество  натуральных  чисел, 

·     Z  —  множество  целых  чисел, 

·     Q  —  множество  рациональных  чисел, 

·     R  —  множество  всех  действительных  чисел. 

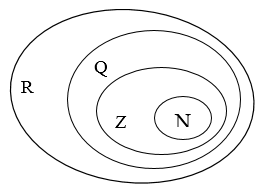
Рисунок  1.  Изображение  множества  действительных  чисел

Что  такое  множество?

В  математике  нет  точного  определения  этого  понятия.  Понятие  «множество»  не  определяется,  оно  поясняется  примерами:  множество  яблок  в  корзине;  множество  точек  отрезка  прямой.  Множество  состоит  из  элементов.  В  приведенных  примерах  —  это  яблоки,  буквы,  точки. 

Множества  обозначаются  заглавными  буквами  латинского  алфавита:  А,  В,  С,  ...  K,  M,  N  …  Х,  ...;  элементы  множества  —  строчными  буквами  алфавита:  а,  в,  с,  ...  k,  m,  n  …  х,  у,  ....  А={а;  в;  с;  d}  —  множество  А  состоит  из  элементов  а,  в,  с,  d,  или,  говорят,  что  элемент  а  принадлежит  множеству  А,  записывается:  аА  (знак    читается:  «принадлежит»).  Элемент  5  не  входит  в  множество  А,  говорят,  что  «5  не  принадлежит  А»:  5  А,  или  .  Если  множество  В  не  содержит  ни  одного  элемента,  то  говорят,  что  оно  пустое,  обозначается:  В=.

Под  множеством  можно  понимать  совокупность  каких-либо  объектов,  называемых  элементами  множества  [1,  с.  18].  Примерами  множеств  могут  быть  и  дома  на  нашей  улице,  и  алфавит  —  совокупность  букв,  и  наш  5  «Д»  класс  —  множество  учеников.

Множества  могут  быть:

·     Конечное  (элементы  которого  можно  пересчитать;  например  —  множество  цифр)

·     Бесконечное  (пересчитать  нельзя;  например  —  песчинки  в  пустыне)

·     Пустое  (не  содержащее  ни  одного  элемента;  например  —  множество  зайцев,  которые  учатся  в  нашем  классе).

Множество  K  называется  подмножеством  множества  N,  если  каждый  элемент  множества  K  является  элементом  множества  N.  Обозначается:  KÍN.  Говорят,  что  множество  K  включается  в  множество  N.

Подмножества  можно  проиллюстрировать  кругами  Эйлера. 

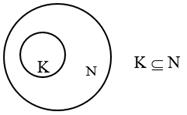
Рисунок  2.  Изображение  подмножества

Действия  с  множествами

В  математике  существуют  несколько  операций  над  множествами.  Мы  разберем  два  из  них:  пересечение  и  объединение.

1.  Пересечение  множеств

Пересечением  множеств  M  и  N  называется  множество,  состоящее  из  элементов,  одновременно  принадлежащих  M  и  N.  Пересечение  множеств  M  и  N  обозначается    [1,  с.  23].

Пример.  Множество  N  =  {  А  Н  Д  Р  Е  Й  }; 

множество  K  =  {  А  Л  Е  К  С  Е  Й  };  множество  M  =  {  Д  М  И  Т  Р  И  Й  }

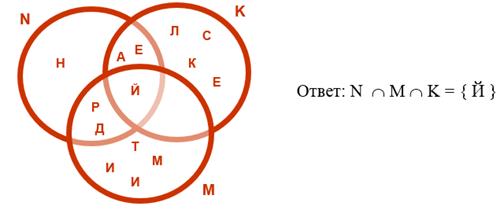
Рисунок  3.  Пример  пересечения  множеств

2.  Объединение  множеств

Объединение  множеств  —  это  множество,  содержащее  в  себе  все  элементы  исходных  множеств.  Объединение  множеств  M  и  N  обозначается  .

Пример  ;  2)  объединение  множества  всех  пород  собак  и  множества  мопсов  есть  множество  всех  собак.

Операции  объединения  и  пересечения  множеств  очень  удобно  показывать  с  помощью  кругов  Эйлера.

По  определению  в  пересечение  двух  множеств  M  и  N  входят  элементы,  принадлежащие  множествам  M  и  N  одновременно

Пример.  Пусть  D  —  множество  из  12  самых  хороших  девочек,  M  —  множество  из  12  самых  умных  мальчиков.  Получили  наш  класс.

Рисунок  4.  Пример  объединения  множеств

3.  Вложенные  множества. 

Пример.  Имеется  три  множества:  «дети»,  «школьники»,  «учащиеся  начальной  школы».  Мы  видим,  что  эти  3  множества  находятся  одно  внутри  другого.  Про  множество,  находящееся  внутри  другого  множества,  говорят,  что  оно  вложенное.

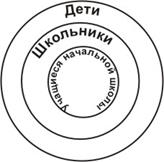
Рисунок  5.  Пример  вложенных  множеств

Задачи,  которые  можно  решить  с  помощью  диаграмм  Эйлера

Задача  №  1

На  стол  бросили  две  салфетки  10  см  х  10  см.  Они  покрыли  площадь  стола,  равную  168.  Какова  площадь  перекрытия?

Решение

1)168  –  10  х  10  =  68;

2)10  х  10  –  68  =  32.

Ответ:  32  см

Рисунок  6.  Рисунок  к  задаче  №  1

Задача  №  2 

В  поход  ходили  80  %  учеников  класса,  а  на  экскурсии  было  60  %,  причем  каждый  был  в  походе  или  на  экскурсии.  Сколько  процентов  класса  были  и  там,  и  там?

Решение

А  —  множество  учеников,  которые  ходили  в  поход

В  —  множество  учеников,  которые  были  на  экскурсии

100  %  –  80  %  =  20  %

60  %  –  20  %  =  40  %

Ответ:  40  %

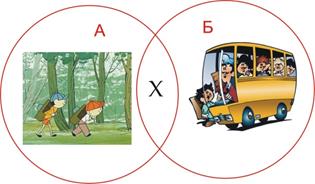
Рисунок  7.  Рисунок  к  задаче  №  2

Задача  №  3

В  нашем  классе  24  ученика.  Все  они  хорошо  провели  зимние  каникулы.10  человек  катались  на  лыжах,  16  ездили  на  каток,  а  12  —  лепили  снеговиков.  Сколько  учеников  смогли  покататься  и  на  лыжах,  и  на  коньках,  и  слепить  снеговика?

А  —  множество  ребят,  катающихся  на  лыжах

В  —  множество  ребят,  катающихся  на  коньках

С  —  множество  ребят,  лепивших  снеговиков

Решение

Пусть  х  —  число  ребят, 

которые  успели  за  эти  каникулы  всё!

(12  -  х)  +  (16  -  х)  +  (10  -  х)  +  х  =  24

Ответ:  7  ребят

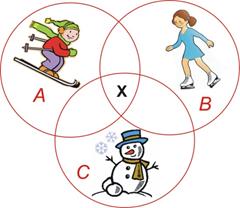
Рисунок  8.  Рисунок  к  задаче  №  3

Задача  №  4

9  моих  друзей  любят  бананы,  8  –  апельсины,  а  7  –  сливы,  5  –  бананы  и  апельсины,  3  –  бананы  и  сливы,  4  –  апельсины  и  сливы,  2  –  бананы,  апельсины  и  сливы.  Сколько  у  меня  друзей?

Решение

5  –  2  =  3  3  –  2  =  1  4  –  2  =  2

9  –  6  =  3  8  –  7  =  1  7  –  5  =  2

3  +  1  +  2  +  3  +  2  +  1  +  2  =  14

Ответ:  14  друзей

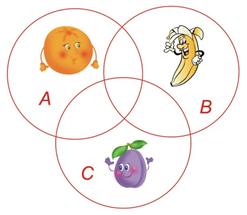
Рисунок  9.  Рисунок  к  задаче  №  4

Задача  №  5

В  пионерском  лагере  «Дубки»  в  смене  актива  отдыхали:  30  отличников,  28  победителей  олимпиад  и  42  спортсмена.  10  человек  были  и  отличниками  и  победителями  олимпиад,  5  —  отличниками  и  спортсменами,  8  —  спортсменами  и  победителями  олимпиад,  3  —  и  отличники,  и  спортсмены,  и  победители  олимпиад.

Сколько  ребят  отдыхали  в  лагере? 

А  —  множество  отличников

В  —  множество  победителей  олимпиад 

С  —  множество  спортсменов

Решение

10  –  3  =  7  5  –  3  =  2  8  –  3  =  5

30  –  12  =  18  28  –  15  =  13  42  –  10  =  32

18  +  13  +  32  +  7  +  2  +  5  +  3  =  80

Ответ:  80  ребят

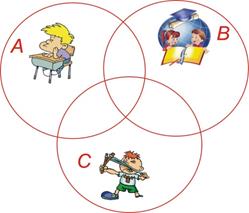
Рисунок  10.  Рисунок  к  задаче  №  5

3.  Заключение

Диаграммы  Эйлера  —  это  общее  название  целого  ряда  способов  графической  иллюстрации ,  широко  используемых  в  различных  областях  математики:  теория  множеств,  теория  вероятностей,  логика,  статистика,  компьютерные  науки,  и  др.  Применение  кругов  Эйлера  позволяет  даже  пятикласснику  легко  решать  задачи,  которые  обычным  путем  решаются  только  в  старших  классах.

Список  литературы:

1.Александрова  Р.А.,  Потапов  А.М.  Элементы  теории  множеств  и  математической  логики.  Практикум  /  Калининград.  1997.  —  66  с. 

2.Депман  И.Я.,  Виленкин  Н.Я.  За  страницами  учебника  математики.  Пособие  для  учащихся  5—6  кл.  М.:  Просвещение,  1999.  с.  189—191,  231.

3.Задачи  для  внеклассной  работы  по  математике  в  V—VI  классах:  Пособие  для  учителей  /  Сост.  В.Ю.  Сафонова.  Под  ред.  Д.Б.  Фукса,  А.Л.  Гавронского.  М.:  МИРОС,  1993.  —  с.  42. 

4.Занимательная  математика.  5—11  классы.  Как  сделать  уроки  нескучными  /  Авт.  сост.  Т.Д.  Гаврилова.  Волгоград:  Учитель,  2005.  —  с.  32—38. 

5.Смыкалова  Е.В.  Дополнительные  главы  по  математике  для  учащихся  5  класса.  СПб:  СМИО  Пресс,  2009.  —  с.  14—20. 

6.Энциклопедия  для  детей.  Т.  11.  Математика  Глав.ред.  М.Д.  Аксёнова.  М.:  Аванта  +,  2001.  —  с.  537—542.