ПРОВЕДЕНИЕ  ОБЩЕЙ  КАСАТЕЛЬНОЙ  К  ГРАФИКАМ  ДВУХ  КВАДРАТИЧНЫХ  ФУНКЦИЙ

Мисякова  Виктория

Протас  Надежда

Класс  10  «Д»,  лицей  БНТУ,  Республика  Беларусь,  г.  Минск

Лях  Алла  Сатуриновна

научный  руководитель,  преподаватель  математики,  лицей  БНТУ,  Республика  Беларусь,  г.  Минск

.(*)

У  данных  квадратичных  функций  старшие  коэффициенты  равны  1  и  -1,  т.  е.  ветви  обеих  парабол  направлены  в  разные  стороны.  Для  определения  точек  пересечения  графиков  приравняем  правые  части  уравнений  системы  (  ⃰⃰  )  и 

исследуем  взаимное  расположение  графиков  заданных  кривых  при  различных  значениях  их  коэффициентов    и  .

1)  Если  ,  то  параболы  имеют  две  общие  точки.

2)  Если  ,  то  параболы  имеют  одну  общую  точку  (касаются  друг  друга).

3)  Если  ,  то  параболы  не  имеют  общих  точек.

Теперь  проведем  общие  касательные  к  параболам:

  —  уравнение  касательной.

Пусть  общая  касательная  касается  параболы    в  точке  ,  а  параболы    —  в  точке  (рис.  1):

Рисунок  1.

Напишем  уравнение  касательной  для  кривой  :

Напишем  уравнение  касательной  для  кривой  :

Условие  полного  совпадения  двух  касательных  есть  равенство  соответствующих  коэффициентов:

Таким  образом,  мы  имеем  систему  уравнений:

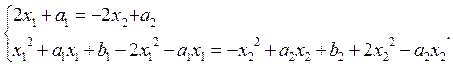
В  результате  преобразований  получим  уравнение:

.

1)  Если  ,  то  параболы  имеют  две  общие  точки  и  в  этом  случае  невозможно  провести  общую  касательную.

Вывод:   для  парабол,  у  которых  старшие  коэффициенты  равны  1  и  -1  и    (параболы  имеют  две  общие  точки),  общей  касательной  не  существует.

Пример  1:

(рис.  2).

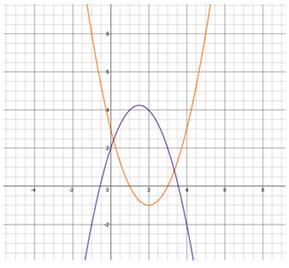
Рисунок  2.

2)  Если  ,  то  параболы  имеют  одну  общую  точку  (касаются  друг  друга)  и  в  этом  случае  существует  единственная  общая  касательная,  проведенная  в  точке  касания  парабол    —  точка  касания.

Уравнение  общей  касательной  имеет  вид:

Вывод:   для  парабол,  у  которых  старшие  коэффициенты  равны  1  и  -1  и  ,  (параболы  будут  иметь  одну  общую  точку  касания),  можно  провести  одну  общую  касательную  в  их  точке  касания.

Пример  2:

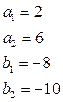  (рис.  3).

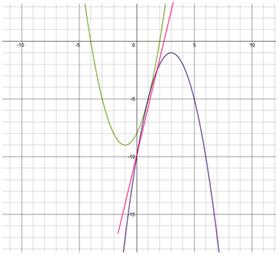
Рисунок  3.

Уравнение  касательной  и  точка  касания:

3)  Если  ,  то  параболы  не  имеют  общих  точек  и  в  этом  случае  можно  провести  две  общие  касательные.

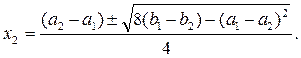
Обозначим  А  и  С  точки  касания  графиков  парабол  в  одном  случае,  В  и  D  –  в  другом. 

Тогда:

;

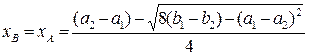.  (рис.4)

Рисунок  4.

Уравнения  общих  касательных  имеет  вид:

Для  прямой  AC:

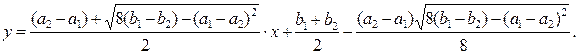
Для  прямой  BD: 

Заметим,  что  четыре  точки  касания  двух  общих  касательных  образуют  четырехугольник  ABCD,  у  которого  стороны  AB  и  CD  параллельны. 

Докажем,  что  данный  четырехугольник  является  параллелограммом.

Пусть  точка  М₁  —  середина  отрезка  АС,  а  точка  М₂  —  середина  отрезка  ВD.  Тогда 

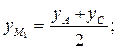
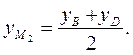
Получим 

Так  как  координаты  точек  M₁  и  M₂  совпадают,  то  четырехугольник  АBCD  -  параллелограмм.

Вывод:   для  парабол,  у  которых  старшие  коэффициенты  равны  1  и  -1  и  ,  (параболы  не  будут  иметь  общих  точек),  можно  провести  две  общие  касательные,  и  точки  касания  будут  являться  вершинами  параллелограмма,  две  стороны  которого  параллельны  оси  ординат.

Пример  3:

  (рис.  5)

Рисунок  5.

Уравнения  касательных  и  точки  касания:

;

;

;

.

Список  литературы:

1.Атанасян  Л.С.,  Бутузов  В.Ф.,  Кадомцев  С.Б.  Геометрия.  Дополнительные  главы  к  учебнику  9  класса  М.:  Вита-Пресс,  2003.  —  176  с.;

2.Энциклопедический  словарь  юного  математика.  Сост.  Савин  А.П.  М.:  Педагогика,  1985.  —  352  с.;