С  ГИПЕРБОЛОЙ  К  ЗВЕЗДАМ

Скрипкин  Владимир

класс  8»А»  МБОУ  «Лицей  №  6  имени  М.А.  Булатова»,  РФ,  г.  Курск

Басенко  Наталия  Владимировна

научный  руководитель,  учитель  математики  МБОУ  «Лицей  №  6  имени  М.А.  Булатова»,  РФ,  г.  Курск

Евдокимова  Мария  Дмитриевна

научный  руководитель,студент  факультета  «Прикладная  математика  и  физика»,  каф.  «Математическая  кибернетика»,  гр.  8О-305Б,  Московский  авиационный  институт  (национальный  исследовательский  университет),  РФ,  г.  Москва

Взгляните  ясным  вечером  на  небо.  Где-то  мелькают  огоньки  самолета,  звук  которого  совсем  не  слышен,  или  далеко-далеко  светится  какая-то  точка.  Может  это  спутник?  Хочется  поближе  это  увидеть,  прикоснуться…  В  ноябре  этого  года  мне  посчастливилось  попасть  в  XIV  Нижне-архызскую  осеннюю  астрономическую  школу  «Специальной  астрофизической  обсерватории  РАН».  Там  на  меня  произвели  большое  впечатление  телескопы  системы  Кассегрена-Шмидта.  На  практических  занятиях  мы  наблюдали  за  различными  космическими  источниками  света.  Интересно  то,  что  телескопах  используются  зеркала  и  линзы,  которые  имеют  форму  гиперболы.  Да,  той  самой  гиперболы,  которую  мы  изучаем  на  уроках  математики.

Меня  очень  заинтересовал  этот  вопрос.  И  я  поставил  себе  следующие  цели  и  задачи:

1.  изучить  основные  свойства  гиперболы,  определить,  как  меняется  вид  гиперболы  в  зависимости  от  значений  ее  параметров; 

2.  проверить  актуальность  данной  тематики  и  узнать,  насколько  окружающим  интересны  эти  вопросы;

3.  разработать  лабораторный  практикум  по  построению  гиперболы  различными  способами:  в  технике  «оригами»,  геометрическими  построениями,  с  помощью  программного  продукта;

4.  попробовать  описать  свойства  двуполостных  гиперболоидов  вращения,  используемых  в  телескопах  и  антеннах  системы  Кассегрена,  Хаббла. 

Итак,  гипербола  (рис.1).  Пересечём  конус  плоскостью,  параллельной  его  оси,  но  не  проходящей  через  вершину  конуса.  Мы  получим  кривую,  это  и  есть  гипербола. 

По  определению  гипербола  это  геометрическое  место  точек,  разность  расстояний  от  каждой  из  которых  до  двух  точек  той  же  плоскости  F1  и  F2,  называемых  фокусами,  есть  величина  постоянная,  равная  2а.

Гиперболу  можно  задать  с  помощью  канонического  уравнения  вида 

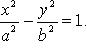
К  такому  виду  можно  свести  уравнение  второй  степени,  используя  формулы  сокращенного  умножения.  Покажем  это  на  конкретном  примере:

x²-y²-8x  -2y+11=0

(x²-8x+16)-16-(y²+2y+1)+1+11=0   (x-4)²  -  (y+1)²=4

Получим

(x-4)²/4  -  (y+1)²/4  =  1

Построить  гиперболу  можно  различными  способами.  Например,  используя  линии  сгибов  при  определенном  складывании  бумаги  (техника  оригами),  или  с  помощью  циркуля  и  линейки  (рис2).  Пошаговое  построение  дает  интересную  «картинку».

Рисунок  1.  Гипербола

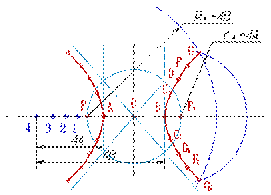
Рисунок  2.  Пошаговое  построение  гиперболы

Но  «ручная  работа»  всегда  утомительна  и  неточна,  поэтому  мы  с  научными  руководителями  задумались  о  программе  построения  гиперболы.  Знакомясь  с  возможными  существующими  программами,  я  изучил  работу  Елисеева  И.Б.  (г.  Красноярск,  научный  руководитель  Ларин  С.В.)  «АНИМАЦИОННЫЕ  ИЗОБРАЖЕНИЯ  КРИВЫХ  ВТОРОГО  ПОРЯДКА  В  СРЕДЕ  GEOGEBRA».  По  результатам  которой  было  видно,  что  компьютерное  моделирование  позволяет  наглядно  и  просто  перейти  от  пространственного  определения  конических  сечений  к  плоскостным  определениям  кривых  второго  порядка  и  получить  способы  их  построения.  Но  изменение  таких  величин,  как  угол  поворота,  смешение  начала  координат  учитывать  в  программе  тяжело  (требуется  введение  дополнительных  операций).  Поэтому  мы  применили  программный  продукт  С++-приложения  интегрированной  среды  разработки  Microsoft  Visual  Studio  2012.  В  данной  программе  возможно  применение  преобразований,  таких  как  параллельный  перенос  вдоль  координатных  осей  и  поворот.  Программа  обладает  небольшими  аппаратными  требованиями,  высоким  быстродействием  и  гарантированной  устойчивостью  работы.

Результаты  построения  представлены  на  рисунках  (рис.  3).

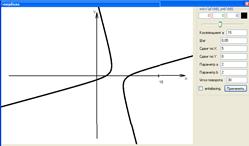
Рисунок  3.  Построение  гиперболы  с  помощью  программного  продукта

Вращая  гиперболу  вокруг  каждой  из  своих  осей,  получают  два  гиперболоида  вращения-однополостной  и  двуполостной.  Однополостной  гиперболоид  как  бы  соткан  из  прямых  линий.  Свойства  однополостного  гиперболоида  использовал  русский  инженер  В.Г.  Шухов  при  строительстве  радиостанции  в  Москве  (башни  Шухова).  Она  состоит  из  нескольких  поставленных  друг  на  друга  однополостных  гиперболоидов.  Также  устроена  и  Эйфелева  башня  в  Париже.

  Свойство  двуполостного  гиперболоида  вращения  отражать  лучи,  направленные  в  один  из  фокусов,  в  другой  фокус,  используется  в  телескопах  системы  Кассегрена  и  в  антеннах  Кассегрена  (рис.  4). 

Рисунок  4.  Схема  работы  телескопов  по  системе  Кассегрена

Свет  приходит  от  опорной  звезды  (естественной  т.  е.  наблюдаемым  объектом  или  искусственной,  созданной  лазерным  лучом),  корректируется  и  направляется  на  аппарат  исследователя  (например,  фотокамеру).

Это  сделано  для  того,  чтобы  при  наблюдениях  все  объекты  были  видны  четко,  без  искажений.

Поле  зрения  системы  таких  телескопов,  как  нам  рассказали,  около  4°  (в  то  время  как  для  телескопов  с  зеркалами  в  форме  параболы  6—8°).

На  базе  такой  же  оптической  схемы  (схема  Ричи-Кретьена)  построен  знаменитый  орбитальный  телескоп  Хаббл. 

По  аналогичному  принципу  работают  и  радиоантенны  Кассегрена.  Они  применяется  для  радаров  и  систем  спутниковой  связи.  Конструкция  антенны  Кассегрена  включает  в  себя  также  гиперболические  зеркала,  в  одном  из  фокусов  которого  расположен  излучатель.  Размеры  излучателя  можно  менять.  Это  позволяет  разрабатывать  разные  конструкции  антенн.

Вот  сколько  интересного  связано  с  гиперболой!  И  как  показал  он-лайн-опрос  в  социальных  сетях,  интересно  было  не  только  нам.  (60  %  опрошенных  проявили  интерес  к  изучению  «интересных»  свойств  гиперболы)

Оказывается,  эта  кривая  второго  порядка  крайне  необходима  и  на  Земле  и  в  космических  пространствах.  И  если  скорость  спутника  увеличить  до  11,1  км/с  он  навсегда  уйдёт  от  Земли,  двигаясь  в  глубины  Вселенной  тоже  по  гиперболе!

Список  литературы:

1.Акопян  А.В.  Геометрические  свойства  кривых  второго  порядка  М.:  МЦНМО,  2007.  —  136  с.

2.Вокруг  гиперболы.  Математический  клуб  «Кенгуру».  Выпуск  №  11.  Составители  Жарковская  Н.А.,  Рисс  Е.А.  СПб.:  «Левша.  Санкт-Петербург»  —  28  с.

3.Шилдт  Г.  Базовый  курс  по  С++;  изд-во  «Вильямс»,  2008.  —  610  с.

4.Шилдт  Г.  Справочник  программиста  по  С/С++;  изд  –во  «Вильямс»,  2006.  —  800  с.