Статья опубликована в рамках: X Международной научно-практической конференции «Проба пера» (Россия, г. Новосибирск, 26 ноября 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ДОКАЗАТЕЛЬСТВ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ТРЕУГОЛЬНИКОВ
Кузиванов Дмитрий
Класс 10, школа МАОУ «Гимназия при Главе МР «Сосногорск», РФ, г. Сосногорск
Кузиванова Надежда Ивановна
научный руководитель, педагог высшей категории, учитель математики МБОУ «Кадетская школа», РФ, г. Сосногорск
Исследовательская работа посвящена вычислению площади треугольника.
Актуальность исследования обусловлена ежегодным усложнением заданий ЕГЭ, что требует углубленных знаний не только в алгебре, но и геометрии.
Цель: доказать и исследовать различные формулы для вычисления площади треугольника.
Формулы для площади треугольника, составленные и доказанные в данной работе, применимы не только для нахождения площади, но и для отыскания других элементов фигур (угла, стороны, периметра и радиуса, вписанной, вневписанной и описанной окружностей).
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
Доказательство этих формул приводить не будем, оно известно большинству учеников.
4. ![]() . Доказательство.
. Доказательство. ![]()
![]() (рисунок 1).
(рисунок 1).
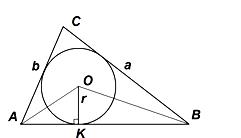
Рисунок 1.
5. ![]() . Доказательство. Воспользуемся формулой
. Доказательство. Воспользуемся формулой ![]() . Для этого умножим на 2 и возведём в квадрат обе части равенства:
. Для этого умножим на 2 и возведём в квадрат обе части равенства: ![]() или
или ![]() .
.
6. ![]() .
.
Доказательство . Воспользуемся формулой Герона: ![]() ;
; ![]() . Следовательно,
. Следовательно, ![]() .
.
7. ![]() . Доказательство. По теореме синусов
. Доказательство. По теореме синусов ![]() и применяя формулу (2), получим:
и применяя формулу (2), получим: ![]() .
.
8. ![]() . Доказательство. По теореме синусов
. Доказательство. По теореме синусов ![]() . Используя формулу (2), имеем:
. Используя формулу (2), имеем: ![]() .
.
9. ![]() . Доказательство. Из теоремы синусов имеем (рисунок 1):
. Доказательство. Из теоремы синусов имеем (рисунок 1): ![]()
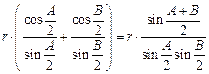 . Учитывая, что
. Учитывая, что ![]() и
и ![]() , получим:
, получим: 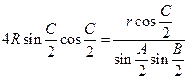 ;
; ![]() . Подставляя в формулу (8) имеем:
. Подставляя в формулу (8) имеем: 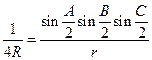 , получим:
, получим: ![]() .
.
10. ![]() . Доказательство. Из прямоугольного ∆AOK:
. Доказательство. Из прямоугольного ∆AOK: ![]() , из прямоугольного ∆COK:
, из прямоугольного ∆COK: ![]() (рисунок 1). Складывая эти равенства, получаем:
(рисунок 1). Складывая эти равенства, получаем: ![]() . Аналогично можно получить, что
. Аналогично можно получить, что ![]() и
и ![]() . Используя формулу (4), получим:
. Используя формулу (4), получим: ![]() .
.
11. ![]() . Доказательство.
. Доказательство. ![]() (рисунок 2). По второй формуле имеем:
(рисунок 2). По второй формуле имеем: ![]() . Аналогично:
. Аналогично: ![]() и
и ![]() . Следовательно:
. Следовательно: ![]() .
.
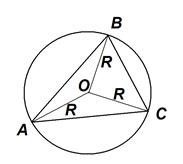
Рисунок 2.
12. ![]() . Доказательство. По теореме косинусов:
. Доказательство. По теореме косинусов: ![]()
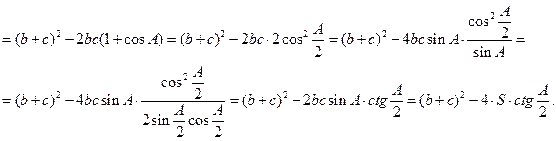
Имеем: ![]() Следовательно:
Следовательно: ![]() Отсюда находим площадь треугольника:
Отсюда находим площадь треугольника: ![]() .
.
13. ![]() . Доказательство. По теореме синусов имеем:
. Доказательство. По теореме синусов имеем: ![]() . Поэтому, используя формулу (2), получим:
. Поэтому, используя формулу (2), получим: ![]() .
.
§ 2. Площадь треугольника, связанная с элементами вневписанной окружности
Вспомогательная задача. Доказать, что а) 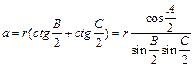 ;
;
б) 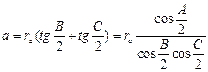 ; в)
; в) ![]() ; г)
; г) ![]() .
.
Доказательство . Пусть вписанная окружность касается стороны ВС в точке К, а вневписанная – в точке L (рисунок 3). Тогда ВС = ВК + КС =![]() и ВС = ВL + LC =
и ВС = ВL + LC =![]() LB
LB![]() +
+ ![]() LC
LC![]() =
= ![]() . Кроме того р–b = ВК =
. Кроме того р–b = ВК = ![]() и р – b=СL=
и р – b=СL= ![]() . Если вневписанная окружность касается продолжений сторон АВ и АС в точках P и Q, то р = АР =АQ =
. Если вневписанная окружность касается продолжений сторон АВ и АС в точках P и Q, то р = АР =АQ = ![]()
![]() .
.
14. ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Доказательство. ![]()
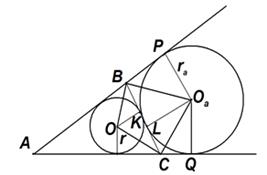
Рисунок 3.
15. ![]() . Доказательство. Согласно задаче
. Доказательство. Согласно задаче ![]() =
=![]() и
и ![]() =
=![]() ;
; ![]() =
=![]() и
и ![]() р. Перемножая эти пары равенств, получаем р(р-a)=
р. Перемножая эти пары равенств, получаем р(р-a)=![]() и (р–в)(р–с) = и подставляя в формулу Герона, получаем исходную.
и (р–в)(р–с) = и подставляя в формулу Герона, получаем исходную.
16. ![]() . Доказательство. Согласно задаче
. Доказательство. Согласно задаче ![]() и
и ![]() . Подставляя в формулу
. Подставляя в формулу ![]() , получаем исходную.
, получаем исходную.
17. ![]() . Доказательство. Согласно задаче
. Доказательство. Согласно задаче ![]() и
и ![]() =
= ![]() . Перемножая эти равенства, получаем rp =
. Перемножая эти равенства, получаем rp = ![]() , следовательно
, следовательно ![]() . Аналогично,
. Аналогично, ![]() . Поэтому
. Поэтому ![]() и
и ![]() , а значит,
, а значит, ![]() .
.
18. а)![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Доказательство . Согласно задаче (приложение 1) р = АР =АQ = ![]()
![]() . Используя формулу
. Используя формулу ![]() , получаем
, получаем ![]() .
.
19. ![]() . Доказательство. Согласно задаче
. Доказательство. Согласно задаче ![]() ;
; ![]() и
и ![]() . Перемножая эти равенства, получаем
. Перемножая эти равенства, получаем ![]() . Подставляя в формулу Герона будем иметь:
. Подставляя в формулу Герона будем иметь: ![]()
![]() . Следовательно,
. Следовательно, ![]() .
.
20. 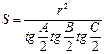 . Доказательство. Используя формулы:
. Доказательство. Используя формулы: 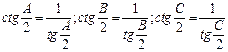 , нетрудно получить исходную формулу.
, нетрудно получить исходную формулу.
21. ![]() . Доказательство. Эту формулу несложно получить, используя задачу и формулу (6). Имеем:
. Доказательство. Эту формулу несложно получить, используя задачу и формулу (6). Имеем: ![]() , тогда
, тогда ![]() .
.
Мы самостоятельно составили и доказали формулы площади треугольника, которые можно использовать в задачах для нахождения неизвестных величин.
Геометрический материал этой работы богат и многообразен, его можно использовать на факультативах учащихся, интересующихся математикой.
Список литературы:
1.Андреев П.П., Шувалова Э.З. Геометрия, М.: «Наука» 1975, — с. 101—109.
2.Гейдман Б.П. Издательство Московского Центра непрерывности математического образования. Москва 2001, — с. 6—20.
3.Шавулова Э.З., Каплун В.И. Геометрия, М.: «Высшая школа» 1980, — с. 120—126.
дипломов

Комментарии (18)
Оставить комментарий