Статья опубликована в рамках: VII Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 07 мая 2013 г.)
Наука: Математика
Секция: Геометрия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИКА В ГЕОГРАФИИ
Гурова Валерия
класс 11 «Б», МОУ гимназия № 11, г. Волгоград
Резниченко Дарья Анатольевна
научный руководитель, учитель первой категории, учитель математики и информатики, МОУ гимназия № 11, г. Волгоград
Введение
Математика и география. Казалось бы, как две эти науки взаимосвязаны между с собой? Некоторые ученые до сих пор скептически относятся к симбиозу этих двух наук. Резонанс мнений исследователей велик, от восторженных взглядов до недоверчивых мыслей на слияние двух дисциплин. Первое использование математических методов относят к временам Эратосфена и Фалеса Милетского. Тогда «Царица наук» использовалась для вычисления астрономических и геодезических задач. В эпоху Великих географических открытий математика также не имела популярность среди географов, так как основной чертой этого времени было непосредственно изучение и открытие новых территорий. Что нельзя сказать о начале XX века. Ученые стали внедрять математику в географию. Многие деятели науки даже создали школы по статической обработке наблюдений.
Объект исследования
Математические методы в географии.
Цель исследования
Изучение применения математических методов при решении задач географического характера.
Причины слияния двух наук.
Как было сказано во введении, внедрение математических методов в решение географических задач не являлось каким-то новаторством, присущим именно для нынешнего времени. Математизация географии произошла уже давно, имев немного другую направленность. Пик изучения математики через географическую призму приходится на 1950—1960 гг. Для многих ученых применение математических алгоритмов в географии явилось новым направлением в данной дисциплине. Но вопреки мнению большинства, часть деятелей науки продолжали видеть нецелесообразность синтеза географии и математики. В 1970-х г. даже стали появляться работы, в которых высказывалась подобная мысль.
Арманд Давид Львович — основоположник изучения географии с помощью математических методов в России. На данный момент в данной дисциплине используются различные методы математического алгоритма. Основным аспектом внедрения математики является необходимость обобщения, полученной за многие годы информации.
В наши дни математика используется для географического прогноза, что помогает получать более правдивые сведения. Но так ли все просто? Нет. Существует ряд причин препятствующих безупречному развитию математики в географии, такие как: отсутствие прочной базы знаний по использованию математических алгоритмов у специалистов; малая официализация знаний и понятий; порой, протекающие природные явления, очень трудно описать математическим языком.
Математизация в наши дни.
Казалось бы, описание разнообразных явлений и теорий путем географического анализа достаточно. Но стремительный рост хозяйственной деятельности стал проявлять все более острую необходимость в точном познании, в более глубоком освоении науки. Поэтому ученым-географам не оставалось выхода, кроме как привлекать разные отрасли науки в географию и способствовать их взаимодействию. Использование математических алгоритмов дало возможность:
1. беспрепятственно вычислять количество жителей в пределах определенного ареала обитания и прогнозировать рост населения;
2. вычислять густоту расселения, площадь государства (города);
3. определять масштаб;
4. измерять высоту гор, находить абсолютную высоту, определять температуру на вершине.
Но математический метод работы дал возможность не только определять географические объекты, но и выявлять математические закономерности. Это предоставило более обширные знания о циклонах и антициклонах, о выборе строительной площадки для возведения здания, о паводках вследствие выпадения осадков, которые могут оказаться губительными, если не предпринимать меры по безопасности.
Все геосистемы взаимосвязаны между собой. Более ярким этому доказательством является развитие знаний в области математического моделирования. С появлением этого метода устройство географических систем двигается вперед с невероятной скоростью. Метод математического моделирования заключается в изображении различных природных явлений путем выражения математических формул, а так же для имитации процессов природы. Чем же удобен процесс моделирования? Ответ очень прост. Математическое моделирование отсеивает второстепенные факторы, предоставляя внимаю лишь те, которые необходимы.
В географии широко применяются три разновидности математических моделей:
1. Построенные без учета пространственного координирования явлений. Результаты осуществления, которых не подлежат картографированию;
2. Модели, результаты которых подлежат картографированию, но пространственное положение учитывается на этапе выполнения математических алгоритмов;
3. Модели, в которых невозможно осуществить математические расчеты без учета пространственного аспекта.
Так же выделяют различные этапы использования метода моделирования:
1. Для анализа, полученных данных;
2. Для систематизации, собранных фактов;
3. Для описания природных явлений;
4. Для прогноза дальнейшего развития ситуации.
В большей степени в разделах географии можно обнаружить использование статистики и теорий вероятности.
Методы математического моделирования в географии.
Смысл метода моделирования в географии заключается в изучении каких-либо явлений, природных процессов, а также целых природных систем, путем создания и исследования полученной модели (рисунок 1). Имеются несколько типов моделей:
1. Пространственно-подобные (материальные) модели. Создаются человеком из различных материалов с учетом всех геометрических правил;
2. логические (идеальные) модели. К ним относятся теории, правила, законы, понятия;
3. образные (фото, зарисовки);
4. знаковые модели;
5. образно-знаковые.
Рисунок 1. Копия горы Маттерхорна (высота образа 25 нм) — Альпийская гора с высотой 4478 м, с масштабом 1:5*109
С помощью применения математического моделирования разрешаются такие вопросы, как:
1. систематизация полученной информации;
2. оценка рельефных особенностей местности;
3. постройка ГИС;
4. автоматическое зонирование, картирование и классификация;
5. управление и прогнозирование явлений с географической точки зрения;
6. оценка антропогенного воздействия на экосистемы;
Если рассматривать физическую географию, то особое место отведено графическим и математическим моделям. Чаще всего методы математического анализа встречаются в экономической географии. Спектр использования математики именно в экономической географии шире, нежели в физической.
Использование математического моделирования в экономической географии.
1.Модель центральных мест Вальтера Кристаллера.
Данная теория, издавшаяся в 1933 г. предлагала наилучшее расположение городов (Схема 1).
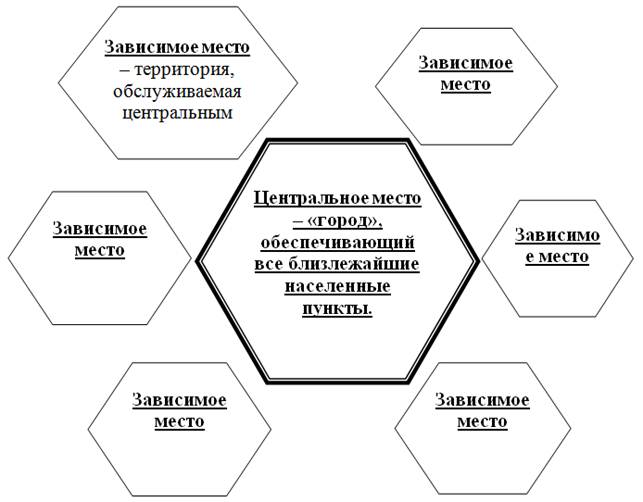
Схема 1. Модель центральных мест Вальтера Кристаллера
Создав абстракционную модель, Вальтер пытался рассмотреть ее в масштабах Европы. Используя данную теорию, освоить незастроенные территории. Но реальное пространство весьма неоднородно. Ведь такие факторы, как транспорт, рельеф, население играют, действительно, важную роль, но задача заключается в определении спроса и предложения на товары, поэтому данную модель можно «упростить». Для данной теории упрощение заключается в том, что для необходимой территории берется ровный рельеф, плодородная почва, однородное распределение жителей с одинаковыми спросами и предпочтениями, движение транспорта в любом направлении. Теорию центральных мест можно назвать идеальной. В этой местности расходы по снабжению населения находятся в зависимости от расстояния между местом, где товар произведен и населенным пунктом. С ростом издержек спрос на большинство товаров уменьшается. Очевидно, что с увеличением расстояния спрос на товар будет уменьшаться до тех пор, пока не достигнет нулевой отметки (точки, в которой на соответствующие товары и услуги не найдется ни одного потребителя). Вследствие того, что расстояние пропорционально транспортным расходам, а также жители распределены равномерно, то зона сбыта будет иметь форму круга; место, производящее товары будет называться «центральным местом», а поселения, куда снабжается товар «зависимым местом»
Изначально, Вальтер Кристаллер разделил изучаемый район на окружности. При таком дроблении участка, возникают некоторые сложности: если, окружности касаются друг друга, то появляются игнорируемые территории, но если окружности пересекают друг друга, вследствие заполнения района, то образуются зоны загораживания. Поэтому форма районов сбыта — шестиугольник. Они равномерно заполняют всю территорию. По углам шестигранника находятся районы сбыта, в центре непосредственно город, производящий продукцию. Размеры района могут отличатся друг от друга. Зависят они от спроса.
Так как количество подчиненных зон равняется шести, то во внимание берется предположение, что независимо от центрального или зависимого положения, при максимальной потребности в каком-либо товаре одним поселением, каждый район сбыта будет иметь по семь единиц спроса(шесть зависимых + одно центральное). Это называется «k-оценки» центрального места. На данный момент k=7.
Также можно спрогнозировать и другую ситуацию. Когда потребители зависимых мест, не все ориентированы на какое-то одно центральное место. Например, в каждом зависимом месте спрос на товар может быть разделен между четырьмя центральными местами, тогда k=2,5. Так как каждый из зависимых мест получает по 0,25 единиц спроса и одно центральное место, тогда k=(6*0,25)+1.
Но необходимо также учитывать во внимание и то, что товары и услуги могут иметь разные ценовые показатели. Услуги, имеющие высокий ценовой порог, будут продаваться в меньшем количестве, нежели услуги, имеющие низкий ценовой порог. Как следствием будет являться удаленность центральных мест друг от друга, предлагающих товары по высокой стоимости. Из-за подобного ценового резонанса, возникает иерархия центральных мест. И зависит она не только от предлагаемых товаров, но и от k-оценок.
Но данная теория о центральном месте у многих ученых вызвала недовольство своим «идеальным» моделированием.
Теория промышленного штандорта Альфреда Вебера.
Вопрос о географическом размещении промышленности является насущной проблемой в хозяйственной деятельности человека. Штандортным фактором (фактор размещения) Вебер назвал экономическую выгоду, заключающаяся в сокращении издержек производства и сбыта товаров, то бишь в таком размещении предприятий промышленного характера, что расходы при изготовлении продукции были бы минимальны.
Основная идея теории заключается в том, что заранее задано размещение сырьевой базы (это имеет отношение как к добывающей промышленности, так и к сельскому хозяйству), приближенное к реальности; установлено размещение центров потребления продукции промышленного характера и объемы спроса. При систематизации полученных данных в ходе работы, не учитывается ни заработная плата, ни интенсивность труда.
Суть теории состоит в том, чтобы определить главенствующий фактор размещения (региональный, агломерационный, природно-технический, культурно-общественный) и определить закономерность действия данных факторов.
Для построения общей теории необходимо знание лишь общих факторов регионального характера. Поэтому особо внимание было уделено 7 видам производственных издержек:
1. Издержки на земельную ренту (аренда, покупка).
2. Издержки на основной капитал (здания, машины, оборудование).
3. Издержки на сырье и энергоресурсы.
4. Издержки на рабочую силу.
5. Транспортные издержки.
6. Процент на заемный капитал.
7. Амортизационные отчисления на основной капитал.
Проведя полный анализ каждой из семи издержек, определилось два штандортных фактора:
1. Издержки на рабочую силу.
2. Транспортные издержки.
Издержки на рабочую силу
Рабочие пункты – места, где производительность труда и заработная плата имеют низкие издержки на рабочую силу, — будут притягивать к себе промышленные штандорты с минимальными транспортными издержками.
Смоделировать этот фактор можно графически с помощью изодапан — кривых линий, соединяющих точки с одинаковыми отклонениями от минимальных издержек транспортной ориентации. Если изодапана, соединяющая точку отклонения от минимальных транспортных затрат, равна изодапане, соединяющей точку экономии на трудовые ресурсы, то такая изодапана называется «критической».
Итак, чем выше рабочий коэффициент, тем сильнее концентрация отрасли в том или ином пункте.
Транспортные издержки
Транспортные издержки определяются только двумя факторами: весом транспортируемых грузов и расстоянием перевозки. При вычислении транспортных издержек во внимание берутся издержки по перевозке материалов к местам перевозки, потом готовой продукции к местам ее потребления. Тогда выходит, что фактор размещения этого производства находится в каком-то из этих мест, либо на прямой между ними. Получается, что постоянной величиной станет один из двух элементов транспортных издержек — расстояние, переменной величиной, дифференцирующей общую величину транспортных издержек от места к месту, будет только вес перевозимых грузов.
Для понимания методики расчета всех затрат в теорию введены понятия «склад» — место добычи промышленного сырья и энергетических ресурсов и «штандортная фигура». Тогда для каждого места потребления по каждому виду продукции можно построить геометрическую фигуру, образованную взаиморасположением n-складов и потребительским местом. Это сочетание и названо Вебером «штандортной фигурой», на которую следует опираться к дому производству при выборе места размещения.
При числе «складов» — 2, штандортная фигура образует простой треугольник, вершины которого образованы 2 «складами» и местом потребления данного продукта (М).
Для вычисления наилучшего по транспортным издержкам штандорта следует учесть соотношение издержек на потребляемые локализованные материалы (сырье, топливо) и на отправляемые к месту потребления готовые продукты. Соотношение веса локализованных материалов к весу продукта называется материальным индексом. Общий вес грузов, перевозимых от «материальных складов» к месту производства и от этого места к местам потребления товаров называется штандортным весом.
Если для производства 100 т. какого-либо продукта потребуется 300 т. одного локализованного материала и 200 т. другого локализованного материала, то материальный индекс данного производства (отрасли) будет равен: (300 + 200): 100 = 5. Исходя из этих же величин, штандортный вес в целом будет равен 600, а в расчете на единицу продукции — 6.
Поиск штандорта — оптимального места размещения, ведется в рамках штандортной фигуры следующим образом, «Положим, — пишет Вебер, — мы имеем перед собой производство, работающее с 2 локализованными материалами, причем для выработки 1 т. продукта требуется ¾ т. одного материала и ½ т. другого. В таком случае мы получаем штандортную фигуру на «материальных компонентах» (линиях, соединяющих штандорт с «материальными складами») которого передвигаются веса в 3/4 и 1/2, в то время как «потребительская компонента» отягощена 1,0. Отсюда, исходя из принятого выше допущения, что единственными факторами, определяющими транспортные издержки, служат вес и расстояние, мы приходим к следующему выводу: веса, соответствующие различным компонентам, представляют те силы, с которыми различные вершины углов штандортной фигуры притягивают к себе штандорт производства».
На основе этого подхода с использованием материальных индексов и штандортных весов Вебер проанализировал более сложные случаи расчета штандортных фигур, что позволило ему придти к ряду общих закономерностей, связанных с размещением промышленности при транспортной ориентации.
Заключение.
Сколько новых знаний открывает для нас математика в географии. Все-таки, я считаю, что математизация географии это новые двери, за которыми спрятан огромный кладезь знаний, которые нам еще необходимо изучить.
Список литературы:
1.Масляев В.Н. Методы эколого-географических исследований (конспект лекций) — Саранск: копи-центр «Референт», 2009. — 134 с.
дипломов

Комментарии (2)
Оставить комментарий