Статья опубликована в рамках: VII Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 07 мая 2013 г.)
Наука: Математика
Секция: Геометрия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОД «МАЛЫХ ШЕВЕЛЕНИЙ». РЕШЕНИЕ ЗАДАЧ
Денисова Анастасия
класс 11 «А», МБОУ СОШ с углубленным изучением отдельных предметов № 103, г. Нижний Новгород
Курганова Галина Алексеевна
научный руководитель, педагог высшей категории, преподаватель математики, МБОУ СОШ с углубленным изучением отдельных предметов № 103, г. Нижний Новгород
При испытании геометрических высказываний на правдоподобие, при поиске контрпримеров математик нередко рассуждает так: «Возьму случай, когда высказывание подтверждается, и «пошевелю» одну точку (или отрезок, или какое-либо другое множество точек). Не могу ли я таким способом получить такой случай, когда высказывание не подтверждается?» [1, с. 4]
Задача 1. Из точки Р, расположенной внутри выпуклого многоугольника, опускаются перпендикуляры на его стороны или на их продолжения. Условимся основание такого перпендикуляра называть «приятным», если оно принадлежит стороне, и «неприятным» в противном случае. Верно ли, что всякая внутренняя точка любого многоугольника имеет по крайней мере две приятные проекции?
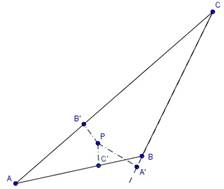
Рисунок 1.Треугольник ABC
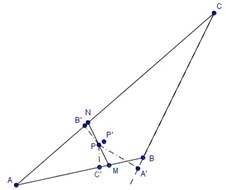
Рисунок 2.Четырехугольник MNCB
Решение:
Возьмем сначала в качестве искомого выпуклого многоугольника треугольник ABC. Если он остроугольный, то все проекции любой его внутренней точки — приятные. Пусть тр. ABC тупоугольный. В этом случае внутри него легко выбрать такую точку Р, у которой будут две приятные проекции (рис. 1). Теперь нетрудно построить выпуклый четырехугольник и точку, лежащую на его контуре, так, чтобы эта точка имела только одну приятную проекцию. Таков, например, четырехугольник MNCB (рис. 2 — MN — любая прямая, оставляющая снаружи проекции А', В', С'). Точка Р на его контуре имеет одну приятную проекцию (этой проекцией будет сама точка Р). Но точка Р не лежит внутри многоугольника MNCB. Поэтому «пошевелим» точку Р — сдвинем ее немного внутрь четырехугольника. При малом «шевелении» точки Р мало пошевелятся и ее проекции. Поэтому при достаточно малом шевелении те проекции, которые были неприятными до шевеления точки Р, останутся такими и после шевеления. Значит, после шевеления точки Р мы получим внутри четырехугольника точку Р', у которой будет ровно одна приятная проекция (а именно — проекция на сторону MN).
Использованный в задаче приём «шевеления» в научной литературе носит название метода «малых шевелений». Прием «малых шевелений» используется для задач, в которых требуется выбрать из некоторого множества фигур ту, которая является наилучшей (берем произвольную фигуру и пытаемся малыми шевелениями ее улучшить, т.е. из нескольких ее свойств изменяем только одно, стараясь сохранить остальные) [1, с. 6], а также в задачах, где требуется рассматривать вариации параметров при определенных неизменных условиях. Идею «малых шевелений» полезно привлечь и тогда, когда в каком-то множестве фигур требуется выбрать (построить, найти) ту, которая в том или ином смысле является «наилучшей» (например, найти наименьший периметр, наибольшую площадь и т. п.). На практике этот метод имеет достаточно широкое применение: это решение задач повышенного уровня сложности (в т. ч. олимпиадных) и планиметрические задачи с неоднозначностью в условии, встречающиеся в Едином Государственном Экзамене РФ.
Задача 2 (олимпиада «Росатом» НИЯУ МИФИ, очный тур, 2013 г.)
Дана полуокружность радиусом 5 см (AO=OB=R). Равнобедренный треугольник EDC (EC=DE, DE — основание) располагается внутри нее так, что сторона EC лежит на диаметре, а вершина D принадлежит полуокружности. EC = 7 см. Найдите максимально возможную длину DC.
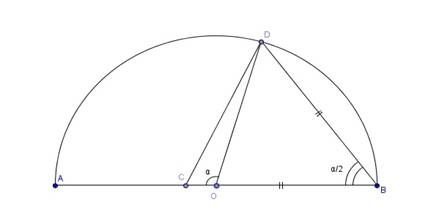
Рисунок 3. Треугольник CBD (CED)
Решение:
1) Методом ММШ несложно убедиться, что наибольшая длина DC достигается, если точка E совпадает с точкой B (рис. 3). Тогда:
OC=BC(EC)-OB(R)=2 (см)
DO=R=5 (см)
2) Пусть угол ![]() , а угол DBC соответственно
, а угол DBC соответственно ![]() (как вписанный и центральный углы, опирающиеся на одну дугу)
(как вписанный и центральный углы, опирающиеся на одну дугу)
3) По теореме косинусов:
![]()
В то же время:
![]()
4) Приравнивая правые части уравнений и подставляя численные значения получаем: ![]() , а так же
, а так же ![]() (данное значение невозможно)
(данное значение невозможно)
5) Подставляя полученное значение ![]() получаем, что DC примерно равно 5,42 (
получаем, что DC примерно равно 5,42 (![]() )
)
Ответ: DC=5,42
Задача 3. В трапеции KLMN известны боковые стороны KL = 36, MN=34 верхнее основание LM =10 и ![]() . Найдите диагональ LN.
. Найдите диагональ LN.
Решение:
1) По условию задачи ![]() , значит
, значит ![]() .
.
2) Из вершины L опустим перпендикуляр к KN (LF).
3) Для вычисления LF найдем синус угла LKF.
![]() ,
, ![]() .
.
4) Проведем LE || MN, E принадлежит KN.
![]()
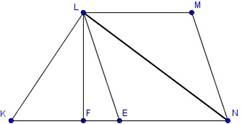
Рисунок 4.Случай 1
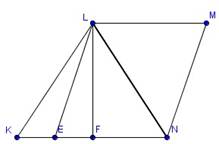
Рисунок 5.Случай 2
Случай первый (рис. 4).
FN = FE+EN = 12, LN=36
Случай второй — передвинем точку N (рис. 5).
Тогда будем иметь:
FN = EN-FN = 8, ![]()
Ответ: 36 или ![]() .
.
Задача 4. Трапеция ABCD с основаниями AD=6 и BC=4 и диагональю BD=7 вписана в окружность . На окружности взята точка К , отличная от точки D так, что BK=7. Найдите длину отрезка АК (рис. 6).
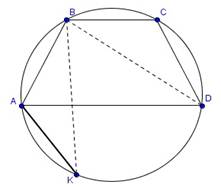
Рисунок 6. Трапеция ABCD
Решение:
1) Равные отрезки стягивают равные дуги, т.е. дуга BD равна дуге BK.
2) Дуга BD = дуга BС + дуга CD; дуга BK = дуга BA + дуга AK
3) Дуги CD и ВА равны (их стягивают стороны р/б трапеции;трапеция равнобедренная, т.к. только около р/б трапеции можно описать окружность), следовательно дуги АК и ВС также равны, т.е. отрезки, стягивающие их имеют одинаковую длину, АК=ВС=4.
Второй случай невозможен, в чем можно убедиться шевелением точки К по окружности при прочих неизменных параметрах.
Ответ: 4.
Таким образом, метод малых шевелений представляет большой интерес, так как с его помощью можно решать, не прилагая больших усилий, геометрические задачи повышенного уровня сложности. Метод помогает улучшить проективное мышление, а также облегчает возможность нахождения инварианта в задачах с неоднозначностью в условии.
Список литературы:
1.Балк Г., Балк М., Болтянский В. — Метод малых шевелений — М.: МЦНМО, журнал «Квант», 1979, № 4.
дипломов

Комментарии (1)
Оставить комментарий