ПРИМЕНЕНИЕ  ТРЕУГОЛЬНИКА  РЁЛО

Артюшкин  Алексей

класс  11  «Б»,  МОУ  гимназия  №  11,  г.  Волгоград

Резниченко  Дарья  Анатольевна

научный  руководитель,  учитель  первой  категории,  учитель  математики  и  информатики,  МОУ  гимназия  №  11,  г.  Волгоград

Актуальность:  в  современном  мире,  при  быстро  развивающихся  технологиях  нельзя  обойти  стороной  фигуру  постоянной  ширины  —  треугольник  Рёло,  позволяющий  сократить  затраты  при  производстве,  к  примеру,  при  конструировании  деталей. 

Объектом  исследования  является  треугольник  Рёло.

Цель  исследования:  привести  достаточное  количество  примеров  применения  свойств  треугольника  Рёло.

Для  решения  поставленной  цели  были  выделены  следующие  задачи  исследования: 

·изучить  главные  свойства  треугольника  Рёло; 

·отсмотреть  видео  материал  про  треугольник  Рёло;

·на  основе  изученных  материалов  предложить  области  использования  треугольника  Рёло. 

Методами  исследования  являются  изучение  документации  и  информационных  материалов,  наблюдение,  анализ,  эксперимент.

Как  и  большинству  подростков  старшего  школьного  возраста  поколения  90-х,  меня  интересуют  спортивные  автомобили.  Особое  внимание  я  уделяю  эксклюзивным  моделям.  Поэтому  сильно  привлекает  моё  внимание  машина  Mazda  RX-7  и  чуть  позже  RX-8,  где  интерес  вызывает  двигатель  этих  машин.  Речь  идет  о  «двигателе  Ванкеля»,  или  о  «роторном  двигателе». 

В  свое  время  Ванкель  сделал  прорыв  в  машинной  индустрии,  создав  двигатель  кардинально  отличавшиеся  от  поршневого.  Главным  отличаем  является  количество  движущихся  частей,  такой  главной  деталью  в  двигателе  будет  ротор.  Только  благодаря  особой  форме  ротора  такой  двигатель  возможен.  Эта  форма  носит  название  —  «Треугольник  Рёло»,  или  в  простонародье  круглый  треугольник  (Рис.1).  Фигура  «треугольник  Рёло»  меня  заинтересовала,  и  я  решил  разобраться  в  её  свойствах  и  способах  применения. 

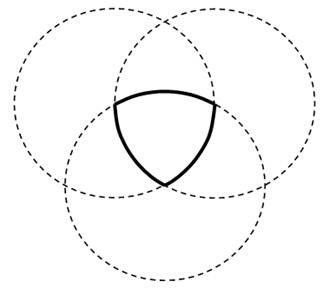
Рисунок  1.  Треугольник  Рёло

Я  начал  с  того,  что  решил  изучить  все  свойства  фигуры.  И  остановиться  на  тех,  которые  помогут  понять,  куда  её  можно  применить.  Первое  —  её  построение.  Такую  фигуру  очень  просто  построить,  используя  только  циркуль.  Для  этого  нужно  провести  две  окружности  с  одинаковым  радиусом,  но  так,  чтобы  центр  второй  совпадал  с  одной  из  точек  первой  (кроме  центра).  Проводим  третью  окружность,  так  что  бы  её  центр  совпадал  с  точкой  пересечения  первых  окружностей  (Рис.  1).  Область,  которая  принадлежит  всем  трем  кругам  и  есть  треугольник  Рёло.

Треугольник  Рёло,  является  фигурой  постоянной  ширины.  Это  означает,  что  если  провести  две  параллельные  прямые  на  некотором  расстоянии,  то  фигура  при  качении  будет  касаться  обеих  прямых  постоянно.  Расстояние  между  ними  и  будет  фигура  постоянной  ширины.  Простейшей  такой  фигурой  будет  всем  известный  круг.  На  самом  деле  таких  фигур  не  мало.  Среди  ряда  таких  фигур  наименьшая  площадь  у  треугольника  Рёло.  Это  утверждение  носит  название  теоремы  Бляшке  —  Лебега.  К  примеру,  если  его  вписать  в  круг,  то  разница  очевидна  (Рис.  2). 

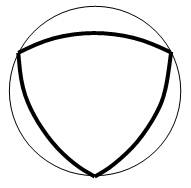
Рисунок  2.  Отношение  площадей

Пусть  а  —  это  ширина  фигуры,  тогда  площадь  ,  а  периметр    (Рис.  3).

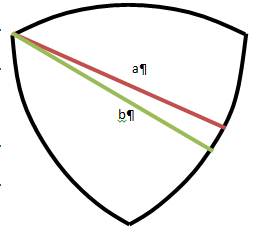
Рисунок  3.  Треугольник  Рёло

Треугольник  Рёло  обладает  тремя  осевыми  линиями,  которые  проходят  из  вершины  в  середину  противоположной  стороны  b.

Являясь  фигурой  постоянной  ширины,  треугольник  Рёло  обладает  всеми  общими  свойствами  фигур  этого  класса.  А  именно:

·с  каждой  из  своих  опорных  прямых,  треугольник  Рёло  имеет  лишь  по  одной  общей  точке;

·расстояние  между  двумя  любыми  точками  треугольника  Рёло  ширины  не  может  превышать  а;

·отрезок,  соединяющий  точки  касания  двух  параллельных  опорных  прямых  к  треугольнику  Рёло,  перпендикулярен  к  этим  опорным  прямым;

·через  любую  точку  границы  треугольника  Рёло  проходит,  по  крайней  мере,  одна  опорная  прямая;

·через  каждую  точку  границы  треугольника  Рёло  проходит  объемлющая  его  окружность  радиуса,  причём  опорная  прямая,  проведённая  к  треугольнику  Рёло  через  точку,  является  касательной  к  этой  окружности;

·радиус  окружности,  имеющей  не  меньше  трёх  общих  точек  с  границей  треугольника  Рёло  ширины,  не  превышает;

·по  теореме  Ханфрида-Ленца  о  множествах  постоянной  ширины  треугольник  Рёло  нельзя  разделить  на  две  фигуры,  диаметр  которых  был  бы  меньше  ширины  самого  треугольника;

·треугольник  Рёло,  как  и  любую  другую  фигуру  постоянной  ширины,  можно  вписать  в  квадрат,  а  также  в  правильный  шестиугольник;

·по  теореме  Барбье  формула  периметра  треугольника  Рёло  справедлива  для  всех  фигур  постоянной  ширины.

Не  опровержим  тот  факт,  что  свойство  треугольника  Рёло  —  качение  по  квадрату,  позволяет  применять  его  в  интересных  областях  (Рис.  4). 

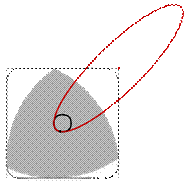
Рисунок  4.  Качение  по  квадрату

Треугольник  Рёло  вписан  в  квадрат  и  может  вращаться  в  нём,  постоянно  касаясь  всех  четырёх  сторон.  Каждая  вершина  треугольника  при  его  вращении  «проходит»  почти  весь  периметр  квадрата,  отклоняясь  от  этой  траектории  лишь  в  углах  —  там  вершина  описывает  дугу  эллипса.  Центр  этого  эллипса  расположен  в  противоположном  углу  квадрата,  а  его  большая  и  малая  оси  повёрнуты  на  угол  в  45°  относительно  сторон  квадрата  и  равны  (Рис.4).  Все  4  эллипса  касаются  смежных  сторон  квадрата  на  расстоянии    от  угла  (Рис.5).

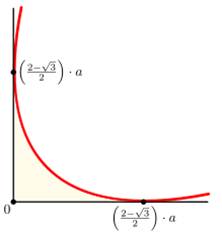
Рисунок  5.

Изучив  научную  и  справочную  литературу  по  треугольнику  Рёло,  я  выделил  4  области  применения  фигуры  постоянной  ширины. 

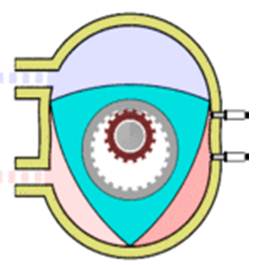
Рисунок  6.  Двигатель  Ванкеля

Во-первых,  это  двигатель  Ванкеля  (Рис.  6),  который  возможен  благодаря  форме  ротора.  Он  вращается  внутри  камеры,  поверхность  которой  выполнена  по  эпитрохоиде[1].  Вал  ротора  жёстко  соединён  с  зубчатым  колесом,  которое  сцеплено  с  неподвижной  шестерёнкой.  Такой  трёхгранный  ротор  обкатывается  вокруг  шестерни,  касаясь  вершинами  внутренних  стенок  двигателя  и  образуя  три  области  переменного  объёма,  каждая  из  которых  по  очереди  является  камерой  сгорания.  Благодаря  этому  двигатель  выполняет  три  полных  рабочих  цикла  за  один  оборот.

Во-вторых,  кинематография,  а  более  точно  —  «Грейферный»  механизм  (Рис.  7),  который  осуществляет  покадровое  перемещение  плёнки  в  кинопроекторах.  В  данном  случае  треугольник  Рёло  находится  внутри  квадрата  и  двигает  рамку,  посредством  вращения  вокруг  одного  из  своих  углов.  Зуб,  который  находиться  на  рамке,  входит  в  перфорацию  киноплёнки,  протаскивает  её  на  один  кадр  вниз  и  выходит  обратно.

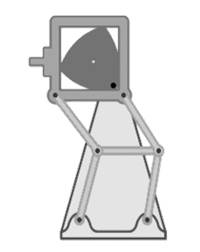
Рисунок  7.  Грейферный  механизм

В-третьих,  с  помощью  сверла  формы  треугольника  Рёло  можно  сверлить  квадратные  отверстия!  Замечено  что  вершины  треугольника  Рёло  описывают  квадрат  только  при  вращение  центра  строго  по  фигуре  состоящей  из  4  дуг  эллипсов  (Рис.4).  Отсюда  и  сложность  создания  такого  сверла,  так  как  обычная  дрель  вращает  сверло  вокруг  своей  оси.  Но  все-таки,  конструкция  позволяющая  воплотить  такое  сверло,  было  придумано  Гарри  Уаттсу  в  1917  году  (Рис.  8). 

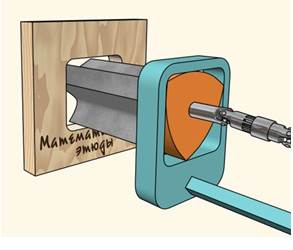
Рисунок  8.  Сверло  Уаттсу

В-четвертых,  это  медиатор  музыкантов-струнников,  а  так  же  диаграммы  Эйлера  RGB.

Основываясь  на  теоретических  данных,  предполагаю,  что  свойства  треугольника  Рёло  возможно  использовать  в  следующих  направлениях:

1.  Создание  и  использование  машины  для  дробления  камней  в  шахтах.  Для  этого  необходимо  изготовить  два  вала,  которые  при  фронтальном  срезе  будут  в  форме  треугольника  Рёло,  причем  вершины  треугольника  имеют  зубья,  глубина  которых  равна  разнице  расстояния  от  центра  до  вершины,  и  расстоянию  от  центра  до  самой  удаленной  точки  на  стороне  (Рис.  9). 

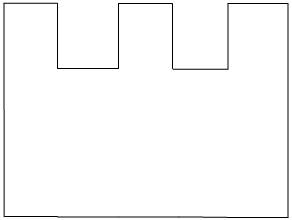
Рисунок  9.  Вал  дробильной  машины  (вид  сбоку)

Которые  надо  расположить  таким  образом,  что  их  оси  будут  находиться  на  расстоянии,  равном  двум  расстояниям  от  самой  удаленной  точки  стороны  треугольника  (назовем  её  х)  до  его  центра,  плюс  15  %  от  этого  расстояния,  и  начать  их  вращать.  При  вращение  мы  будем  наблюдать  две  фазы.  Первая,  когда  точки  х  обоих  валов  будут  на  не  большом  (15  %)  расстоянии  друг  от  друга  (Рис.10),  и  вторая,  когда  зубчатые  вершины  треугольника  Рёло  будут  входить  друг  в  друга  с  небольшим  зазором  (Рис.  11). 

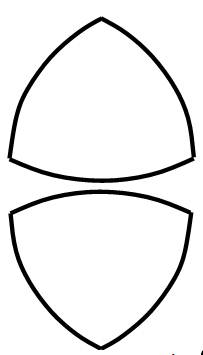
Рисунок  10.  Первая  фаза

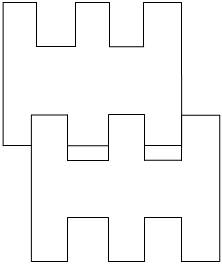
Рисунок  11.  Вторая  фаза

В  первой  фазе  камни  будут  попадать  в  зазор,  а  во  второй  дробиться.  Причем,  если  по  той  же  технологии  расположить  круглые  валы,  то  вероятность  того,  что  конструкция  заклинит  выше,  потому  что  при  вращение  круглых  валов,  всего  одна  фаза,  при  которой  камни  и  попадают  в  дробильный  механизм,  и  дробятся  одновременно.  В  случае  с  машиной,  в  которой  применен  треугольник  Рёло,  фазы  две,  и  даже,  если  при  дроблении  камень  застрял,  то  в  следующей  фазе  механизм  образует  зазор,  и  машина  не  застопорится.  К  тому  же,  современная  дробилка  устроена  таким  образом,  что  в  ней  присутствует  возвратнопоступательный  механизм.  На  примере  сравнения  двигателя  Ванкеля  и  поршневого  двигателя  (и  здесь  можно  выделять  те  же  плюсы).

2.  Тренажеры  для  развития  различных  групп  мышц.  Главная  цель  современных  тренажеров,  это  изолированная  тренировка  мышцы.  Но  время  не  стоит  на  месте  и  биомеханика,  позволила  понять,  что  важно  не  только  изолировать  мышцу,  но  и  правильно  давать  на  нее  нагрузку.  Так  как  мышца  не  способна  одинаково  сильно  работать  на  протяжении  всего  своего  «рабочего  хода»,  то  надо  давать  слабую  нагрузку  в  момент,  когда  она  находиться  в  одном  из  крайних  положений  и  когда  она  проходит  «центральное»  положение,  нагрузка  может  возрастать.  Но  такого  эффекта  сложно  добиться,  для  этого  используют  различные  кулачковоблочные  механизмы,  и  такие  тренажеры  отличаются  дороговизной.  В  свою  очередь  использования  треугольника  Рёло  для  этой  цели  очень  эффективно  заменяет  все  сложные  механизмы.  Работая  пятое  лето  подряд  у  отца  на  заводе  по  изготовлению  тренажеров,  и  занимаясь  последние  два  лета  непосредственно  разработкой  такого  вида  тренажеров,  как  никто  другой,  я  знаю,  как  сложно  создать  такой  механизм.  И  вот  теперь  я  произвел  расчеты,  что,  если  тянуть  трос  не  через  кулачковоблочный  механизм,  а  через  блок  в  виде  треугольника  Рёло,  то  экономиться  приблизительно  2  метра  троса  который  проходит  через  такую  систему,  и  сокращается  расход  метала.  А  результат  изменения  нагрузки  будет  таким  же,  нагрузка  будет  с  начало  возрастать,  а  затем  она  станет  пиковой  в  момент  прохождения  вершины  треугольника  Рёло,  а  затем  снова  сходить  на  нет,  при  условии,  что  мы  тянули  один  и  тот  же  вес.  Нагрузка  на  мышцу  получилась  плавная  и  равномерная.

3.  Люки  канализации.  Фигура  постоянной  ширины  не  может  проходить  через  отверстие  такой  же  фигуры  с  меньшей  шириной.  Благодаря  чему  можно  треугольник  Рёло  использовать  и  в  этом  направление  тоже.  Тут,  конечно,  можно  рассуждать,  что  и  круглый  люк  не  проваливается,  так  как  круг  тоже  фигура  постоянной  величины,  но  нам  уже  известен  тот  факт,  что  у  треугольника  Рёло  меньше  площадь,  чем  у  круга,  а  значит  и  материала  меньше  расходуется  на  крышку  люка.  Это  придумал  не  я.  Но  я  думаю  это  актуально  и  сейчас. 

4.  Музыкальные  инструменты.  Я  окончил  музыкальную  школу  по  классу  баян.  Поэтому  знаю,  какие  минусы  есть  у  моего  инструмента.  Один  из  них  это,  что  при  нажатии  на  клавиши  близко  стоящие  во  2  и  3  ряду  они  цепляют  друг  за  друга  в  виду  небольшого  смешения,  что  не  приемлемо.  Если  же  клавиши  сделать  в  форме  треугольника  Рёло,  и  расположить  их,  как  показано  на  рисунке  12,  то  такой  проблемы  можно  избежать.  Причем  инструмент  будет  более  экстравагантный. 

Рисунок  12.Клавиши  баяна

5.  Также  нашел  применение  треугольника  Рёло  в  мотоиндустрии.  Сам  я,  с  недавних  пор,  увлекся  мотоциклами,  и,  соответственно,  туда  тоже  применил  эту  фигуру.  Всем  известно,  для  того,  чтобы  приводить  мотоцикл  в  движение  необходимо  «крутить  ручку  газа».  В  мотоиндустрии  проблема  с  хорошим  хватом  этой  ручки  стоит  остро.  Её  решали  по-разному,  к  примеру:  используя  материалы,  повышающие  трение  между  перчаткой  и  грипсой  (ручкой  газа).  К  тому  же,  при  длительной  езде  рука  попросту  устает.  Ради  решения  моей  проблемы,  я  изготовил  из  дерева  ручку,  которая  при  фронтальном  разрезе  имела  форму  треугольника  Рёло  и,  как  оказалось,  она  идеально  повторяет  внутренние  контуры  закрытой  ладони,  и  удерживать  такую  рукоять  гораздо  легче.  Как  оказалось,  при  простейшем  изучении  вашей  ладони  вы  увидите,  что  если  собрать  руку  «трубочкой»,  как  будто  вы  держите  что-нибудь  круглое,  то  вторая  и  третья  фаланга  второго,  третьего  и  четвертого,  а  также  вторая  фаланга  первого  пальца  (замыкающего  «кольцо»  из  вашей  ладони)  образуют  вершины  круглого  треугольника,  что  полностью  доказывает  мою  гипотезу.  Данное  открытие  можно  использовать  не  только  для  ручек  мотоцикла,  но  и  везде  где  необходимо  удерживать  с  сопротивлением  поворотную  рукоять  такого  типа.

На  самом  деле,  треугольник  Рёло  называется  так  не  по  праву.  Потому  что  сам  Рёло,  только  описал  и  изучил  круглый  треугольник,  но  никак  не  придумал  его.  Это  легко  проверить,  заглянув  в  работы  Леонардо-де  Винчи.  Еще  можно  встретить  эту  фигуру  в  архитектуре  ранее. 

Что  же  я  получили  в  ходе  работы?  Изучив  литературу,  просмотрев  видео  материалы,  рассмотрев  большое  количество  областей,  которые  укладываются  в  мой  кругозор,  где  только  возможно  применение  треугольника  Рёло,  мы  получили  интересный  результат.  А  заключается  он  в  том,  что  применение  данного  треугольника  в  окружающем  нас  мире,  может  быть  гораздо  большем,  чем  мы  могли  бы  подумать.  Я  считаю,  что  нельзя  так  беззаботно  обходить  треугольник  Рёло,  его  можно  использовать  в  различных  механизмах.  Это  подобно  великому  русскому  языку.  Ведь  столько  слов,  которые  мы  можем  использовать,  не  заимствуя  их  с  других  языков.  Не  применяя  русские  слова,  мы  используем  иностранные.  Так,  не  учитывая  во  внимание  существование  данной  фигуры,  мы  стараемся  изобрести  что-то  новое.  А  так  ли  это  необходимо?  Не  всегда.  Иногда  необходимо  лишь  углубить  свои  знания  в  той  или  иной  области.  И  ответ  окажется  очень  простым.  Знание  о  треугольнике  Рёло,  действительно  облегчает  нашу  жизнь.

Список  литературы:

1.Радемахер  Г.,  Тёплиц  О.  Кривые  постоянной  ширины  //  Числа  и  фигуры.  Опыты  математического  мышления  /  Пер.  с  нем.  В.И.  Контовта.  —  М.:  Физматгиз,  1962.  —  С.  195—211.  —  263  с.  —  («Библиотека  математического  кружка»,  выпуск  10).  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://ru.wikipedia.org/wiki/Треугольник_Рёло  (дата  обращения  22.04.13).