Статья опубликована в рамках: VII Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 07 мая 2013 г.)
Наука: Математика
Секция: Алгебра
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ НА УРОКАХ МАТЕМАТИКИ
Резникова Ольга
обучающая 1 курса 12 группы ГБОУ СПО РО РТТС, г. Ростов-на-Дону
Сидельник Анна Игоревна
научный руководитель, преподаватель математики, ГБОУ СПО РО РТТС, г. Ростов-на-Дону
Занимательные задачи формируют у учащихся логическое мышление и математическую культуру. И под определением «занимательное» подразумевается нечто интересное и увлекательное, с необычным сюжетом. Занимательной можно считать задачу, содержащую занимательные элементы в структуре задачи, или в содержании задачи, или в иллюстрации к задаче. К занимательным можно отнести задачи на перекладывание элементов или переливания, на отгадывание задуманного числа или зачеркнутой цифры, на составления магических квадратов, задачи на подсчет количества элементов фигуры или самих фигур, задачи, связанные с шахматными фигурами, и т. д. [8—9] Любая математическая задача, в том числе и задача на смекалку, для какого бы возраста она ни предназначалась, несет в себе определенную умственную нагрузку, которая чаще всего замаскирована занимательным сюжетом, данными или условием задачи и т. д.
Изучая различный задачный материал по математике [1—7], мы встретились с достаточно большим количеством таких задач, особенно много занимательных задач встречается в математических олимпиадах. Однако в учебниках и задачниках для общеобразовательных школ таких задач не очень много, хотя их наличие могло бы способствовать повышению познавательного интереса. И поскольку в большинстве случаев решение занимательных и нестандартных задач находится далеко не сразу, а только после ряда попыток, то это вырабатывает и настойчивость в достижении цели.
Многообразие занимательного материала — игр, задач, головоломок, позволяет классифицировать занимательные задачи на несколько различных типов (диаграмма 1):

Диаграмма 1. «Классификация занимательных задач»
Рассмотрим подробнее некоторые из данных видов задач.
Исторические задачи
Поскольку история обогащает математическую науку, активизирует умственную деятельность учащихся, особый интерес представляют исторические математические задачи — это задачи, которые решались различными народами в разные времена и эпохи, и способствующие развитию мышления, памяти, воображения и представления. Прежде всего задача воспитывает своим текстовым содержанием. Содержание многих математических задач существенно изменяется в различные периоды развития общества. Так, в русских дореволюционных задачах, которые решали школьники, сюжетное содержание многих математических задач связано с вопросами получения выгоды при купле и перепродаже товара, расчетов выигрыша-проигрыша в азартной игре, хозяйственными вопросами того времени и т. п. Совсем иное сюжетное содержание у задач в современных учебниках: в них сюжет направлен на воспитание у учащихся высоких моральных качеств, научного мировоззрения, на то, чтобы показать связь математики с повседневной жизнью. В качестве примера исторической задачи можно рассмотреть следующую задачу: «Два человека хотят купить корову. Говорит первый второму: «Если ты дашь мне две трети твоих денег, то я смогу один заплатить ее цену». А второй отвечает первому: «Ели же ты мне дашь три четверти твоих денег, то и я заплачу ее цену». Сколько у каждого денег, если корова стоит 24 рубля?».
Задачи на спичках
Обычно мы привыкли к использованию спичек в быту и хозяйственных нуждах, однако стоит отметить еще одну их важную сторону — коробок спичек — отличное пособие для математических развлечений — это задачи, в которых для достижения требуемого результата необходимо совершать манипуляции со спичками. Чаще всего такие задачи предполагают задания на перекладывание спичек из исходной конфигурации данных в новую, чтобы получить нужную фигуру. Несомненно, задачи со спичками развивают быстроту и логичность мышления, память и внимание. Примером может служить следующая задача: «Как из трех спичек сделать число девять?»
Задачи-шутки
Задачи-шутки — это игровые задачи с математическим смыслом, для решения которых нужно проявить скорее находчивость, смекалку, понимание юмора, нежели познания в математике. К таким задачам можно отнести следующую задачу: «По небу летели птицы: воробей, стрекоза, ласточка и шмель. Сколько всего летело птиц?»
Рассмотрим занимательную многоуровневую задачу, которую можно использовать как для учащихся младших, так и для учеников средних и старших классов: «Посчитать количество квадратов и прямоугольников на рисунках (рис. 1—4)».
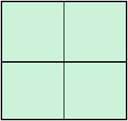
Рисунок 1.
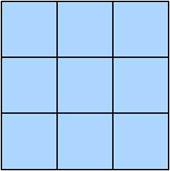
Рисунок 2.
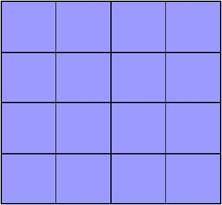
Рисунок 3.
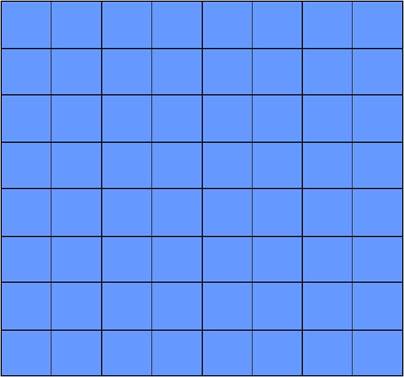
Рисунок 4.
При подсчете можно увидеть, что на первом рисунке квадратиков со стороной в 1 клеточку всего 4, но есть еще один квадрат — его сторона 2 клеточки. Итого квадратов получается пять. При подсчете прямоугольников, следует догадаться, что прямоугольники, которые являются квадратами уже посчитаны – их 5, осталось посчитать прямоугольники. Не трудно заметить, что их 4. Итого получаем, что прямоугольников на рисунке 9. Аналогичные подсчеты следует провести и при нахождении фигур со второго рисунка. Получим, что на втором рисунке 14 квадратов и 36 прямоугольников.
При подсчете фигур с рисунков 3 и 4 можно заметить некоторую закономерность.
Обозначив Ккв. — количество квадратов на рисунке, Кпр. — количество прямоугольников, получим
в квадрате размера 2х2: ![]()
в квадрате размера 3х3: 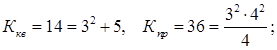
в квадрате размера 4х4: 
в квадрате размера 5х5: 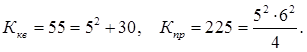
Таким образом, можно вывести общую формулу для нахождения квадратов и прямоугольников, изображенных на рисунках:
![]()
![]()
Учебные задания занимательного характера ценны тем, что они наряду с развитием интереса к обучению способствуют также определенному накоплению учебных знаний, умений и навыков. Лучше усваиваются те знания, которые изучаются с интересом. Благодаря этому учебный навык, на формирование которого направлено это задание, вырабатывается быстрее, т. к. он связан с продуктивной мыслительной деятельностью ученика.
Список литературы:
1.Алимов Ш.А. . Алгебра: учеб. для 7 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
2.Алимов Ш.А. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
3.Алимов Ш.А. Алгебра: учеб. для 7 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
4.Алимов Ш.А. Алгебра и начала математического анализа: учеб. для 10—11 кл. общеобразоват. учреждений. — М.: Просвещение, 2010.
5.Атанасян Л.С. Геометрия: учеб. для 7—9 кл. общеобразоват. учреждений. — М.: Просвещение, 2010.
6.Атанасян Л.С. Геометрия: учеб. для 10—11 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
7.Виленкин В.Я. Математика: учеб. для 5 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
8.Виленкин В.Я. Математика: учеб. для 6 кл. общеобразоват. учреждений. — М.: Просвещение, 2011.
9.Михайлова И.А. Технология историзации школьного математического образования. — Ростов-н/Д., 2009.
10.Мордкович А.Г. Алгебра и начала математического анализа: задачник для 10—11 кл. общеобразоват. учреждений. — М.: Мнемозина, 2010.
11.Олехник С.Н. Старинные занимательные задачи. М.: «Наука», 1995 г.
12.Перельман Я.И. Занимательные задачи и опыты. М.: «Знание»,1992 г.
отправлен участнику

Комментарии (3)
Оставить комментарий