Статья опубликована в рамках: V Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 12 марта 2013 г.)
Наука: Математика
Секция: Геометрия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ОБОБЩЕНИЕ ПОНЯТИЯ ПАРАЛЛЕЛЬНОСТИ
Осокина Елизавета
класс 10 «Б», лицей-интернат «Лидер», г. Волгоград
Коломиец Тамара Владимировна
научный руководитель, педагог высшей категории, преподаватель математики, лицей-интернат «Лидер», г. Волгоград
В окружающем нас мире, мы повсеместно сталкиваемся с параллельными кривыми: железнодорожные рельсы, следы автомобиля на снегу, фрезерование по шаблону, а так же с кривыми преследования, свойства которых применяются при строительстве дорог, горных серпантинов, парков, гоночных трасс и т. д. Чтобы проектировать такие объекты или автоматизировано управлять прогрессивными технологическими процессами промышленного производства, необходимо математическое описание этих объектов или процессов. Итак, нам предстоит ввести понятие параллельных кривых и кривой преследования. В разных источниках можно встретить разные формулировки указанных понятий. Мы считаем, что определение параллельных кривых и кривой преследования нуждается в дальнейшем рассмотрении, доработке и формулировке точного полного определения.
Цель работы: сформулировать обобщенное определение параллельных кривых, опирающееся на свойство постоянства расстояния между ними, и кривой преследования, исследовать их свойства. Продемонстрировать роль математики в современной жизни и в автоматизации производства на примере движения велосипеда, вывести уравнение кривой следа, оставляемого задним колесом велосипеда.
Если учесть, что прямые это тоже линии, то было бы естественно попытаться перенести понятие параллельности прямых линий на линии кривые. В Интернете такое понятие встречается только в связи с понятием огибающей семейства окружностей. Нам кажется, что это понятие можно расширить и обобщить так, чтобы они описывали и другие кривые, которые можно было бы назвать параллельными. Ниже мы сформулируем эти определения и изучим свойства полученных понятий параллельности.
Свойство параллельных прямых — постоянство расстояния — можно использовать для определения параллельности, как аксиому. Используем это свойство для определения параллельных кривых.
Параллельность кривых в терминах расстояния
Дадим два возможных определения параллельности кривых, аналогичные определениям параллельности прямых.
·Если любая точка, принадлежащая кривой b находится на расстоянии r до кривой а, то кривую b назовём параллельной к а.
·Если любая точка, принадлежащая кривой b находится на расстоянии r до кривой а, и любая точка, принадлежащая кривой а находится на расстоянии r до кривой b то кривые а и b назовём параллельными.
При замене в этих определениях слова «кривая» на слово «прямая” мы получим эквивалентные определения параллельных прямых. Так ли это для кривых? Для ответа на вопрос, уточним понятие расстояния от точки до кривой.
Расстояние между двумя множествами, согласно wikipedia, это
![]() ,
,
что следует понимать как «точную нижнюю грань расстояний между точками ![]() и
и ![]() ». Расстояние от точки до кривой — наименьшее из расстояний между этой точкой и произвольной точкой на кривой. Очевидно, что такое расстояние следует измерять как отрезок перпендикуляра, опущенного из точки на кривую. А перпендикуляр к кривой — это перпендикуляр к касательной в точке основания перпендикуляра. Уравнение касательной [1] в точке (x,y) имеет вид Y = f′(x)(X – x) + f(x), а уравнение нормали (перпендикулярной прямой): Y = -
». Расстояние от точки до кривой — наименьшее из расстояний между этой точкой и произвольной точкой на кривой. Очевидно, что такое расстояние следует измерять как отрезок перпендикуляра, опущенного из точки на кривую. А перпендикуляр к кривой — это перпендикуляр к касательной в точке основания перпендикуляра. Уравнение касательной [1] в точке (x,y) имеет вид Y = f′(x)(X – x) + f(x), а уравнение нормали (перпендикулярной прямой): Y = - ![]() (X – x) + f(x).
(X – x) + f(x).
Теперь для каждой точки 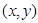 кривой y = f(x), найдём точки, отстоящие от неё на расстояние R. Ясно, что таких точек на нормали будет две по разные стороны от кривой. Выберем на нормали пару векторов длины R, направленных в разные стороны.
кривой y = f(x), найдём точки, отстоящие от неё на расстояние R. Ясно, что таких точек на нормали будет две по разные стороны от кривой. Выберем на нормали пару векторов длины R, направленных в разные стороны.
Векторы 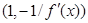 и
и  будут параллельны нормали и разнонаправлены. Сделаем их нужной длины. Для этого поделим их на их длину
будут параллельны нормали и разнонаправлены. Сделаем их нужной длины. Для этого поделим их на их длину
и умножим на R. Окончательно, искомые вектора будут иметь такие координаты:
(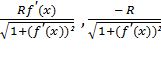 ) и (
) и (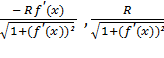 ).
).
Если к точке 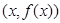 прибавить эти векторы, то мы найдём точки, отстоящие от исходной кривой на расстояние R, т. е. точки двух параллельных кривых к данной кривой. При этом мы получим параметрическое задание параллельных кривых, с параметром
прибавить эти векторы, то мы найдём точки, отстоящие от исходной кривой на расстояние R, т. е. точки двух параллельных кривых к данной кривой. При этом мы получим параметрическое задание параллельных кривых, с параметром 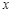 . Вот эти уравнения:
. Вот эти уравнения:
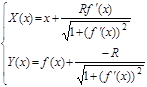 и
и 
В качестве примера рассмотрим параболу y = x²,
здесь 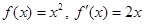 , поэтому уравнения параллельных кривых имеют вид
, поэтому уравнения параллельных кривых имеют вид
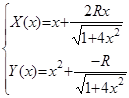 и
и 
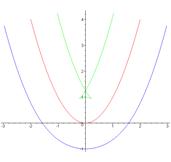
Ниже приведены графики этих кривых, выполненные на компьютере (рис.1)
Рисунок 1.
На графике мы наблюдаем «ласточкин хвост», который оказывается к исходной кривой на расстоянии ближе чем R=1. Следовательно, для параболы глобально не существует верхней параллельной кривой, удовлетворяющей нашим определениям. Нижняя же параллельная существует. Легко найти локальные дуги, для которых существуют обе параллельные: (рис.2—4)
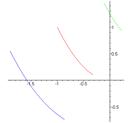


Рисунок 2. Рисунок 3. Рисунок 4.
Наложение этих дуг на одну систему координат и составляет «ласточкин хвост». Ничего подобного среди множества параллельных прямых мы не наблюдаем.
Кривые преследования
Проблемой так называемых «кривых преследования» занимался еще в 1732 г. Пьер Буге. Он опубликовал мемуар «О новых кривых, которые могут быть названы кривыми преследования». Задача состояла в определении кривой, по которой должно двигаться судно, преследующее другое судно, совершающее прямолинейное движение, если отношение скоростей судов постоянно. Такую кривую Буге назвал «кривой преследования» (в работах XIX в. эта кривая именовалась «погонной линией» или «собачьей кривой») или «кривой погони» [6].
Представим себе, что мы наблюдаем за движением велосипеда. Его переднее и заднее колеса соединены негнущейся рамой, которая имеет определенную длину R. Переднее колесо является рулевым и движется по некоторой кривой, а заднее следует за ним по какой-то иной траектории. Выясним, как эти кривые связаны между собой.
Очевидно, что расстояние между задним и передним колесом всегда будет одинаковым. Значит в любой момент времени две точки кривых, которые образуются следами задних и передних колес, будут равноудалены друг от друга. Принятого в научной литературе и на «бескрайних просторах Интернета» названия для таких кривых мы не нашли, поэтому предлагаем свои.
Назовем кривую, которую образует след заднего колеса, кривой преследования, а след переднего — ведущей кривой. Попробуем сформулировать определение для пары описанных кривых.
Определение. Пусть отрезок [B,A] фиксированной длины движется так, что точка A описывает кривую a, а точка ![]() перемещается за точкой A в направлении вектора
перемещается за точкой A в направлении вектора ![]() . Кривую β, которую описывает точка
. Кривую β, которую описывает точка ![]() , назовём кривой преследования, а кривую a — ведущей кривой.
, назовём кривой преследования, а кривую a — ведущей кривой.
Если кривая a является прямой, то кривая преследования будет являться трактрисой. Эта кривая математикам хорошо известна.
Изучим зависимость кривой преследования от ведущей кривой и рассмотрим некоторые её свойства. Ответим на вопрос, однозначно ли определяет кривая a кривую β
Кривая преследования не будет повторять форму ведущей кривой. Более того, они, вообще говоря, не будут даже похожими. Легко себе представить, вспоминая следы велосипеда, что они могут пересекаться, и не раз. Хотя расстояние между соответствующими точками A и B этих кривых будут одинаковы, что позволяет рассматривать их в качестве обобщения понятия параллельных кривых, используя свойство параллельных прямых (постоянство расстояния).
Обобщение введённого понятия можно легко продолжить, соединив несколько отрезков шарнирами в цепочку прицепов.
В реальной жизни определение этой кривой, ее свойства и уравнение может применяться, к примеру, при построении дорог и горных серпантинов. Огромная фура с прицепом, если не учитывать длину прицепа и траекторию его движения, может не вписаться в поворот. Для этого надо либо расширить дорожное полотно, либо сделать радиус кривизны поворота менее заметным. Для крупных дорожных тягачей также надо использовать более широкое дорожное полотно, чтобы они не выезжали за пределы дороги и не способствовали ДТП.
Уравнение кривой преследования
Зададим кривую a уравнением y = f’(x). Bозьмём отрезок [B,A] длины R с концом, лежащим на кривой a, в точке A(x,y) с координатами(x,y), и началом в некоторой точке B(u,v) с координатами. (u,v) Координаты этих точек связаны соотношением
( x – u )² + ( y – x )² = R² (1)
Сделаем бесконечно малый сдвиг точки A(x,y) по кривой ![]() в точку
в точку ![]() . Сдвиг
. Сдвиг ![]() произведён по касательной к a в точке A с тангенсом угла наклона f’(x), следовательно
произведён по касательной к a в точке A с тангенсом угла наклона f’(x), следовательно
Δy ≈ ![]() Δx (2).
Δx (2).
Вызванный этим движением сдвиг ![]() произведён в направлении вектора
произведён в направлении вектора ![]() , поэтому
, поэтому
Δν ≈![]() Δu. (3).
Δu. (3).
Расстояние между точками A’ и B’ равно R, поэтому
(( x – u ) + ( Δx – Δu ))² + (( y – x ) + (Δy - Δν))² = R² (4)
Раскрывая скобки и учитывая равенство (1), получаем
2(x - u)(Δx - Δu) + 2 (y - ν)( Δy - Δν) + (Δx - Δu)² + (Δy - Δν)² = 0 (5)
а после исключения величин ∆y и ∆v равенствами (2) и (3) получаем:
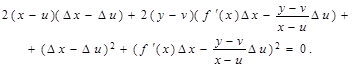
Разделим это равенство на 2∆x
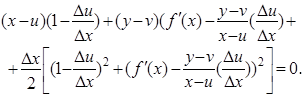
Переходя в этом равенстве к пределу при ![]() и, учитывая, что
и, учитывая, что
![]() ,
,
находим, что
 ,
,
или, после преобразований, получаем систему
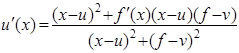 , (6)
, (6)
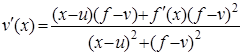 , (7)
, (7)
дифференциальных уравнений, с начальными условиями u(xₒ) = uₒ, ν(xₒ) = νₒ.
Решение этой задачи задаёт траекторию точки B — кривую β.
Если переднее колесо велосипеда будет двигаться по прямой y=0, то система (6)-(7) примет вид

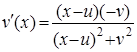 .
.
Решением этой задачи является кривая трактриса.
Примеры кривых преследования и ведущих
1) Ведущая кривая задана уравнением
y = 3 + arctg( x - 3) (рис. 5)
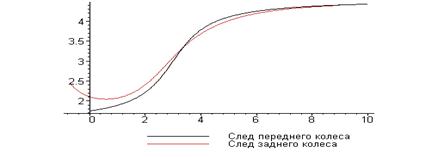
Рисунок 5.
2) Ведущая кривая задана уравнением
y = 5 + sin2x (рис.6)

Рисунок 6.
3) Ведущая кривая задана уравнением: y = 5sin2x (рис.7)
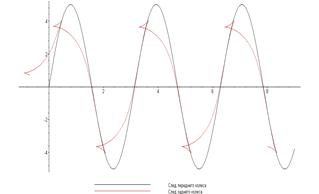
Рисунок 7.
Заключение
1. Множество параллельных кривых, соответствующее нашему определению, существует и является объектом богатым для исследования. Такие исследования мы намерены продолжить.
2. Параллельные кривые в нашем понимании обладают свойствами, существенно отличающимися от свойств параллельных прямых.
3. Предложенное нами определение параллельных кривых, является одним из множества возможных формализаций интуитивного понятия параллельности.
4. В работе мы сформулировали определение «кривой преследования», вывели её формулу и рассмотрели различные виды этой кривой.
Список литературы.
1.Касательная прямая. [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org (дата обращения 16 декабря 2012).
2.Компьютерная графика [Электронный ресурс] — Режим доступа. — URL: http://compgraphics.info
3.Кривая погони. [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org (дата обращения13 декабря 2012).
4.Потоскуев Е.В., Звавич Л.И. Геометрия. 10 кл.: учебник для общеобразоват. учреждений с углубл. и профильным изучением математики. М.: Дрофа, 2010. — 223 с.
5.Трактриса [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org (дата обращения 16 декабря 2012).
6.Яковлев В.И.. Предыстория аналитической механики. Ижевск: НИЦ «Пьер и теория управления кораблем», 2011. — Глава 5.
отправлен участнику

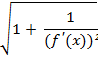
Комментарии (2)
Оставить комментарий