ФЕНОМЕН КРУГЛОГО ТРЕУГОЛЬНИКА

Шорин Алихан

Мачнев Александр

класс 8 «А», комплекс школа-детский сад № 33, г. Караганда

Ковалева Ольга Александровна

научный руководитель, педагог высшей категории, преподаватель математики, Комплекс школа-детский сад № 33, г. Караганда

«Изобретением велосипеда» называют бессмысленное повторение и переоткрытие давно пройденного и известного, и совершенно напрасно. Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. Однажды в интернете я прочитал об одном удивительном изобретении китайского пенсионера — велосипеде с треугольными колесами. Меня заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура — круглый треугольник. Я узнал, что он называется треугольником Рело и посвятил свою работу изучению его свойств и областей применения, поставил задачу выяснить, как геометрия позволяет этому чуду катиться и иметь удивительно плавный ход.

Цель работы — изучить основные свойства треугольника Рело, историю его изобретения, рассмотреть области применения.

Достижение поставленной цели предполагает решение следующих задач:

·     Познакомиться с историей изобретения;

·     Рассмотреть и изучить свойства треугольника Рело;

·     Выяснить области применения треугольника Рело.

·     Найти объяснение плавности хода велосипеда с «треугольными колесами»

Объект исследования: треугольник Рело, как технический феномен.

Предмет исследования: основные свойства треугольника Рело. Методы исследования. Для решения поставленных задач использованы: изучение научной литературы по теме, сбор и систематизация материалов, анализ и интерпретация полученных данных, эмпирические методы.

Гипотеза: Треугольнику Рело присущи свойства обеих геометрических фигур, используемых в его построении, кроме того он обладает собственными свойствами, которые используются в технике.

Структура работы обусловлена целью, задачами и логикой исследования.

В первой главе рассмотрены определение, основные геометрические характеристики и свойства. Треугольник Рёло можно построить, не прибегая к линейке, с помощью одного циркуля. Для этого нужно выбрать произвольно центр первой окружности и провести три равных окружности так, что центр второй — любая точка первой, а центр третьей окружности лежит на пересечении уже построенных окружностей.

1.  Треугольник Рёло — также как и круг — кривая постоянной ширины [1]. Данные утверждения проверены опытным путем, вращением трех геометрических фигур между двумя опорными прямыми:

Рисунок 1. Доказательство постоянства ширины

2.  Периметр треугольника Рело  и совпадает с периметром круга. Формула доказана опытным путем рис. 2, в математике носит название теоремы Барбье [7].

Рисунок 2. Определение периметра круга и треугольника Рело

3.  Площадь. Также как и обычный треугольник, круг, треугольник Рёло является плоской выпуклой геометрической фигурой, которая имеет определенную площадь, которая может быть вычислена по формуле S=(. Формула выведена аналитическим методом, используя соотношение: S=S_cегм, и методом разрезания и сложения площадей (рис. 3). Площадь треугольника Рело меньше площади круга.

Рисунок 3. Определение площади треугольника Рело

4.  Симметричность:

Треугольник Рёло обладает осевой и центральной симметрией

5.  Замечательные точки треугольника

Центры вписанной, описанной окружностей, ортоцентр и центр тяжести совпадают. Сумма радиусов вписанной и описанной окружностей равна ширине треугольника Рело. )a (рис. 4)

Рисунок 4. Замечательные точки

6.  Треугольник Рело можно вписать в квадрат, он может вращаться квадрате со стороной а, всё время касаясь каждой из сторон. В работе рассмотрена траектория движения вершины треугольника при вращении в квадрате и при движении треугольника по прямой. Показано, что так же как и у круга, траектория движения по прямой — циклоида.

Каждая вершина треугольника при его вращении в квадрате «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса [6].

Вывод: Первоначально выдвинутая гипотеза о том, что треугольник Рело, будет сочетать в себе свойства круга и равностороннего треугольника, а также характеризуется только ему присущими свойствами, подтверждена в ходе исследования.

Во второй главе рассмотрены история изобретения треугольника Рело и сферы его применения, дано объяснение плавности хода велосипеда с «треугольными» колесами.

Треугольник Рело назван по имени Франца Рело — немецкого учёного-инженера, подробно исследовавшего его. Однако, впервые эта фигура встречается XV веке в трудах Леонардо да Винчи, созданная им карта мира имеет вид четырех сферических треугольников. Позднее, в XVIII веке встречается идея построения треугольника в трудах Леонардо Эйлера.

Применение треугольника Рело основано на его свойствах. Основные сферы применения в технике: сверло Уаттса (сверление квадратных отверстий), роторно-поршневой двигатель Ванкеля (внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень — треугольник Рело), грейферный механизм в кинопроекторах (используется свойство вращения треугольника Рело в квадрате со стороной ), кулачковые механизмы паровых двигателей, швейных машин и часовых механизмов, катки для транспортировки тяжелых грузов, крышки для люков (свойство постоянной ширины), в качестве медиатора. Кроме того, еще с XIII века используется свойство симметричности и гармонии в архитектурных сооружениях на основе стрельчатых арок и элементов орнамента.

Свойство постоянства ширины использовано и при проектировании велосипеда с «треугольными колесами», повозки с подвеской как на рис. 5. Седло велосипеда при вращении, казалось бы, угловатых колес, остается почти на постоянной высоте относительно земли, качка лишь ненамного превышает привычную. Дабы убедиться, что тряски повозки нет, можно поставить, как учат автомобилистские традиции, на тележку стакан с водой (рис. 5).

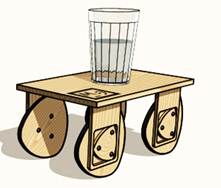
Рисунок 5. Повозка с подвеской на основе треугольника Рело

Заключение

Несколько тысяч лет назад было изобретено колесо, которое произвело переворот в жизни человека. Определяющим свойством, следствием которого стало техническое завоевание им мира, стало свойство постоянства ширины. Но, как оказалось, круг — не единственная фигура, которая обладает этим свойством. Вызвавший мой интерес, треугольник Рело, также принадлежит этому семейству.

В своей работе я не только изучил его свойства, геометрические характеристики, историю изобретения, но и рассмотрел сферы применения этой выпуклой, симметричной фигуры постоянной ширины. Выдвинутая мною гипотеза о свойствах этой фигуры нашла свое подтверждение. Кроме того, я ответил для себя на ряд вопросов познавательного характера: какие геометрические свойства обеспечивают плавность хода велосипеда с «треугольными» колесами, почему канализационные люки делают круглыми или в форме треугольника Рело? Не менее познавательной оказалась информация о сферах применения «круглого» треугольника не только в технике, но и в архитектуре, литературе.

Таким образом, поставленные мною задачи, реализованы в полном объеме.

За рамками представленной работы осталось много интересного: лежащую в основе треугольника Рело, идею построения можно обобщить для построения многоугольников Рело, используя для создания кривых постоянной ширины, не равносторонний треугольник, а звёздчатый многоугольник, образованный отрезками прямых равной длины. Эти направления могут стать перспективой дальнейшей работы. Кроме того, интересным кажется изучение свойств тел постоянной ширины.

Список литературы:

1.Бронштейн И.Н., Семендяев К.А., Справочник по математике для инженеров и учащихся вузов.// — М.:Просвещение,1992.

2.Коксетер С.М., Грейтцер С.Л., Новые встречи с геометрией. // — М., Наука, 1978. — 223 с.

3.Конфорович А.Г., Некоторые математические задачи//. — Киев, Родная школа, 1981. — 189 с.

4.Кушнир И.А., Треугольник в задачах//. — Киев, Лебедь, 1994. — 104 с.

5.Радемахер Г, Тёплиц О. Числа и фигуры — М., Физматгиз, 1962. — 263 с.

6.Треугольник Рёло// Материал из Википедии — свободной энциклопедии [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org/wiki/

7.Яглом И.М., Болтянский В.Г. Фигуры постоянной ширины // Выпуклые фигуры. — М.-Л.: ГТТИ, 1951. — С. 90—105. — 343 с.