ИССЛЕДОВАНИЕ ПОЛОЖЕНИЯ ОРТОЦЕНТРОВ ТРЕУГОЛЬНИКОВ, ВПИСАННЫХ В ГИПЕРБОЛУ

Пятин Илья

10 класс Б школа № 24, г. Северодвинск

Паршева Валентина Васильевна

научный руководитель, заслуженный учитель РФ, учитель математики, школа № 24, г. Северодвинск

Введение

Замечательные геометрические объекты — кривые линии привлекают внимание не только изяществом своей формы, но и многими удивительными свойствами. Одним из таких объектов является гипербола. Эта кривая второго порядка интересна, прежде всего, тем, что это первая линия, которая имеет асимптоты. Эта кривая заинтересовала меня еще и следующим фактом.

Рисунок 1.

В одном старом журнале «Математика в школе! я обнаружил задачу, которая заинтересовала меня: прямые, содержащие высоты треугольника, вписанные в гиперболу y=, пресекаются в точке, лежащей на гиперболе. Сделав соответствующие чертежи в ИГС «Живая геометрия», я пришел к выводу: утверждение верно. Но для достоверности необходимо сделать обоснование. Одновременно возник и другой вопрос: будут ли прямые, содержащие высоты треугольника, вписанного в гиперболу y=, пересекаться в точке, лежащей на этой гиперболе. Графиком функции  является гипербола. Обладают ли указанным свойством кривые, являющиеся графиком дробно-линейной функции?

Проблемные вопросы. Действительно ли прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на гиперболе? Справедливо ли это утверждение для любого выбора вершин треугольника? Чтобы ответить на поставленные вопросы, решил провести собственное исследование данной проблемы.

Цель работы: доказать достоверность утверждения, что прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на гиперболе, или опровергнуть справедливость этого утверждения.

Задачи:

1.  Рассмотреть место положения точек пересечения прямых, содержащих высоты (ортоцентров) треугольников, вписанных в гиперболу вида y = k/x .

2.  Обобщить полученный результат, проведя исследование места положения ортоцентра треугольника, вписанного в гиперболу вида .

Объект исследования: гипербола

Предмет исследования: точки пересечения прямых, содержащих высоты (ортоцентры) треугольников, вписанных в эту кривую.

Методы исследования: построения, выполненные в тетради; компьютерное моделирование, выполненное с помощью интерактивной геометрической среды GeoGebra; аналитические рассуждения.

Гипотеза: Видимо, прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на гиперболе.

Основная часть

Была выдвинута гипотеза: прямые, содержащие высоты треугольника, вписанного в гиперболу , пересекаются в точке, лежащей на этой гиперболе. Выполним моделирование в ИГС GeoGebra.. Гиперболу построим, применяя инструмент «Гипербола», задавая фокусы и одну точку гиперболы

Рисунок 2.

Вершины треугольника DEF принадлежат гиперболе: две вершины — одной ветви гиперболы, третья — другой ветви. Прямые DG и FG содержащие высоты треугольника перпендикулярны прямым FE и DE. Точка G — точка их пересечения лежит на гиперболе.

Будем менять положение вершин треугольника на гиперболе, для чего используем инструмент «Перемещать» Изменяется вид треугольника, но точка пересечения прямых, содержащих высоты треугольника лежит на гиперболе. Изменим гиперболу, выбрав другие фокусы и точку гиперболы. Перемещая вершины треугольника, видим ту же картину. Пусть вершины треугольника принадлежат одной ветви гиперболы. Выполнив необходимые построения, видим, что прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на этой

Компьютерное моделирование в ИГС GeoGebra подтвердило выдвинутую гипотезу: прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на этой же гиперболе. Так ли это на самом деле? Проведем аналитическое доказательство на основании знаний, полученных на уроках алгебры и геометрии.

Первоначально доказательство гипотезы было сделано для гиперболы . Выбирая различные вершины треугольника (точки принадлежат гиперболе) составили уравнения прямых, содержащих стороны треугольника, и уравнения двух прямых, содержащих высоты, нашли координаты ортоцентра и путем подстановки в уравнении гиперболы, убедились, что ортоцентр принадлежит гиперболе. Можно сделать выводы:

1.  Прямые, содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на этой гиперболе;

2.   — координаты этой точки.

Будет ли выдвинутая гипотеза верна для любой гиперболы y=k/x. Зададим треугольник его вершинами:  После рассуждений, аналогичных для гиперболы у=12/х, приходим к выводам:

1.  Прямые содержащие высоты треугольника, вписанные в гиперболу , пересекаются в точке, лежащей на этой гиперболе.

2.  Коорданиты этой точки: , где и  — абсциссы вершин треугольника, вписанного в гиперболу.

Обладают ли таким свойством треугольники, вписанные в кривые, задаваемые уравнением ?

Пример .  . ; ;

Прямая :

    .

Прямая, содержащая высоту треугольника  к стороне

    или .

Прямая :

Прямая, содержащая высоту треугольника  к стороне :

   или

Прямая AC:

Прямая содержащая высоту треугольника ABC к стороне AC:

Найдем точку пересечения прямых, содержащих высоты треугольника  и стороны и , для чего решим систему уравнений:

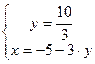
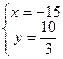
 — искомая точка.

Проверим, принадлежит ли она данной кривой .

Действительно, найденная точка лежит на данной кривой.

Так как графиком функции  является гипербола, то можно сделать общий вывод: прямые содержащие высоты треугольника, вписанного в гиперболу, пересекаются в точке, лежащей на этой гиперболе.

Заключение

В результате проведенного исследования была выполнена цель работы: доказана достоверность утверждения, что прямые, содержащие высоты треугольника, вписанного в гиперболы  и , пересекаются в точке, лежащей на гиперболе.

Выполнение компьютерного моделирования в двух ИГС GeoGebra и «Живая геометрия» позволило сравнить их возможности при выполнении построений.

Для того, чтобы выполнить построения в «Живой геометрии», надо задать уравнение гиперболы, программа сама выполнит ее построение. Чтобы построить прямые, содержащие стороны треугольника, заданными тремя вершинами, лежащими на гиперболе, и прямые, содержащие высоты треугольника, надо сделать соответствующие расчеты по формулам, изученным на уроках математики (составление уравнений прямой по координатам двух точек, составление уравнения прямой, перпендикулярной данной прямой, решение систем уравнений), составить уравнения этих прямых), ввести в программу, и только тогда программа построит чертеж, который будет только иллюстрацией к рассуждениям.

Для того, чтобы выполнить построения в ИГС GeoGebra надо задать уравнение гиперболы, программа сама выполнит ее построение. Далее с помощью инструментов программы строятся все названные прямые. После построения мы можем сразу сделать вывод о расположении точки пересечения прямых, содержащих высоты треугольника. Кроме того, перемещая вершины треугольника вдоль гиперболы, мы можем наблюдать происходящие изменения в чертеже и выдвинуть гипотезу, которую доказать затем математическими расчетами.

В результате проведенного исследования было расширено представление о гиперболе, которое сформулировано в процессе изучения алгебры и геометрии в 8—9 классах, что позволило расширить геометрические представления и углубить знания о гиперболе, установили, что треугольник можно вписать не только в окружность, но и в гиперболу. Компьютерные моделирование и эксперименты позволили повысить уровень работы с ИГС Живая геометрия и GeoGebra, что в свою очередь помогло проведению исследования и осмыслению полученных новых знаний.

Список литературы:

1. Акопян А.В. Геометрические свойства кривых второго порядка — М.: МЦНМО, 2007. — 136 с.;

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. Учебник для 7—9 классов — М.: Просвещение, 2009. — 176 с.;

3. Вокруг гиперболы. Математический клуб «Кенгуру». Выпуск № 11. Составители Жарковская Н.А., Рисс Е.А. — Санкт-Петербург: «Левша. Санкт-Петербург» — 28 с.