КАСАТЕЛЬНЫЕ К ПАРАБОЛЕ

Торопова Анастасия

10 класс Б, школа № 24, г. Северодвинск

Паршева Валентина Васильевна

научный руководитель, заслуженный учитель РФ, учитель математики, школа № 24, г. Северодвинск

Введение

Понятие касательной — одно из важнейших в математическом анализе. «Изучение прямых, касательных к кривым линиям, во многом определили пути развития математики» [2, с. 229]. Но касательную можно провести к различным кривым, в том и числе и к параболе, интерес к которой проявляли древние математики, такие как Апполоний Пергский, Архимед, Папп, Исидор Милетский. Интерес к касательным не ослабевал и у математиков последующих поколений. Исследования, связанные с построением касательных с помощью аналитических методов, проводили Р. Декарт, Г.В. Лейбниц, И. Ньютон.

С помощью циркуля и линейки нетрудно построить касательную к окружности в данной ее точке. В Древней Греции умели строить с помощью циркуля и линейки касательные ко всем коническим сечениям: эллипсам, гиперболам и параболам, что свидетельствует о высоком уровне развития геометрии в то время.

Актуальность работы в том, что понятия касательной к параболе, ее уравнение изучается только в 11 классе, и ее свойства не рассматриваются. В то же время исследование вопроса о касательной к параболе расширяет знания о параболе и круг решаемых задач. Одновременно актуальной является идея применения ИГС GeoGebra для проведения компьютерного моделирования исследуемого вопроса.

Проблемный вопрос: Понятие касательной к кривым вводится в школьном курсе математики только в 11 классе с помощью производной функции. Понятие производной функции возникло на много позже (XVII век) понятий параболы и касательной к ней. Можно ли без понятия производной функции дать определение параболы, сделать вывод ее уравнения и полученные знания применить для построения касательной к параболе?

Цель исследования: применить имеющиеся знания о касательной для исследования новых свойств функции y=x² и попытаться использовать эти свойства для построения касательных к параболе y=x² без вычисления производной.

Задачи исследования

1.Установить геометрическое место точек, являющихся точками пересечения взаимно-перпендикулярных касательных к параболе у=ах².

2.Установить, что касательная к параболе, проходящая через точку А параболы, является прямой, содержащей биссектрису угла, образованного лучом AF, где А — фокус параболы, и перпендикуляром, опущенном из точки А на директрису параболы.

3.Установить, что точки, симметричные фокусу параболы относительно всевозможных ее касательных, расположены на директрисе параболы.

4.Установить, что касательные в концах фокальной хорды параболы пересекаются на директрисе параболы.

5.На основании установленных свойств касательной к параболе выявить способы построения касательной.

Методы исследования

·Анализ школьных учебников математики, математической, справочной литературы, литературы по истории математики.

·Компьютерное моделирование математических объектов с помощью ИГС GeoGebra (компьютерный эксперимент).

·Анализ полученных с помощью компьютерного эксперимента данных.

·Обобщение найденных с помощью компьютерного эксперимента закономерностей.

·Аналитические рассуждения.

Объект исследования: парабола

Предмет исследования: касательные к параболе.

Гипотеза исследования Видимо, касательная к параболе, как любой геометрический объект, имеет свои свойства, которые расширят наши знания о параболе.

Основная часть

В учебной литературе даются такие определения касательной к параболе:

Определение 1. Прямая, имеющая с параболой только одну общую точку и не параллельная ее оси, называется касательной к параболе.

В математическом анализе касательная к кривой в точке М определяется как предельное положение секущей МN при приближении точки N по кривой к точке М.

Определение 2. Касательной к кривой в данной точке МО называется предельное положение секущей М₀М₁ при условии, что точка М₁ стремится к точке М₀ по данной кривой [1, с. 21].

Вывод уравнения касательной к параболе у = ах² в точке М₀ (х₀; ах₀²)

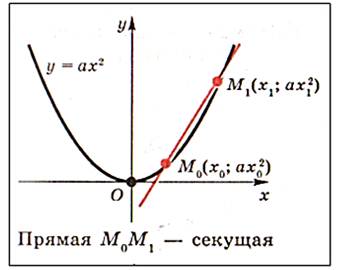
Рисунок 1.

 •Точки М₀(х₀; ах₀²) и М₁(х₁; ах₁²) принадлежат параболе у=ах2. Уравнение секущей М0М1 имеет вид:

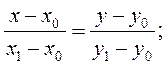
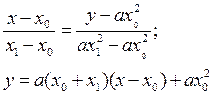
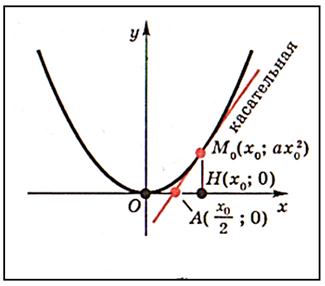
Рисунок 2.

Пусть точка М₁ стремится к точке М₀. Тогда х₁ стремится к х₀ и в пределе уравнение секущей переходит в уравнение касательной в точке М₀(х₀; ах₀²)

Касательная пересекает ось абсцисс в точке А (х₀/2; 0), что следует из уравнения касательной при у=0. Этот факт дает возможность построить касательную к параболе в данной точке М₀ с помощью циркуля и линейки. Для этого нужно провести перпендикуляр М₀Н из данной точки М₀ к оси абсцисс, а затем построить середину отрезка ОН. Это точка А. Проведем прямую через точки А и М₀.

• Прямая АМО является касательной к параболе в данной точке М0.

Построение касательной в ИГС GeoGebra

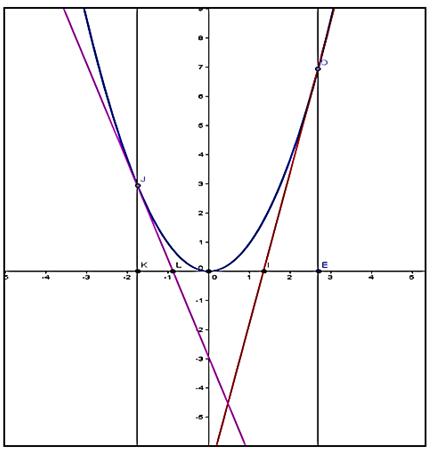
Рисунок 3.

Алгоритм построения с помощь. ИГС аналогичен, только выполняется с помощью инструментов программы:

• перпендикулярная прямая;

• середина или центр;

• прямая по двум точка.

Задача. К параболе y = x² составить уравнения взаимно-перпендикулярных касательных. Найти точку их пересечения.

Решение. Уравнение касательной к параболе y = ax² в точке с абсциссой х₀. Угловой коэффициент этой касательной k₀ = 2ax₀. Уравнение касательной к параболе y = ax² в точке с абсциссой х₁. Угловой коэффициент этой касательной k₁ = 2ax₁.

Найдем соотношение между абсциссами х₀ и х₁. k₀·k₁=-1 — условие перпендикулярности двух прямых. Тогда: 2ax₀∙2ax1 = -1; 4a²x₀x₁ = -1;

Искомое уравнение

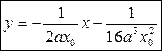
Составим уравнения взаимно-перпендикулярных касательных к параболе у = х² в различных точках, найдем их точки пересечения и сделаем сравнение

Таблица 1.

Выполнив аналогичные рассуждения для параболы у = ах² и сравним координаты точек пересечения взаимно-перпендикулярных касательных к параболе у = ах² можно сделать вывод: абсциссы этих точек разные, а ординаты равны -1/4а, т. е. все такие точки находятся на прямой у = -1/4а, т. е. взаимно-перпендикулярные касательные пересекаются на директрисе параболы.

Возникает вопрос: всегда ли к параболе можно провести две взаимно-перпендикулярных касательных. Ответ очевиден — исключением является вершина параболы.

Теорема параболы. Пусть A — точка на параболе с фокусом F, директриса d, АD — перпендикуляр, опущенный на директрису. Тогда касательной к параболе, проходящей через точку A, будет прямая, содержащая биссектрису угла FAD.

Доказательство. Пусть касательная t в точке M параболы пересекает ее директрису в точке Q и пусть P — основание перпендикуляра, опущенного из точки M на директрису.

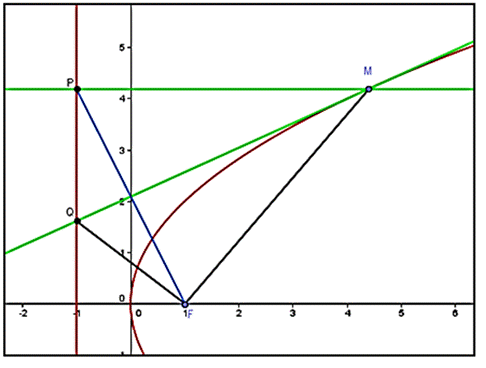
Рисунок 4.

В четырехугольнике MFQP два противолежащих угла — прямые и стороны MP и MF равны. 

Следовательно, ΔPMQ = ΔQMF и касательная t является биссектрисой угла, образованного фокальным радиусом и прямой, проходящей через данную точку параллельно оси x.

Если MP — перпендикуляр, опущенный из точки M параболы на директрису, то биссектриса угла FMP есть касательная к параболе в точке M.

Вывод. Отсюда, далее, следует, что основания перпендикуляров, опущенных из фокуса параболы на ее касательные, принадлежат касательной к параболе в ее вершине.

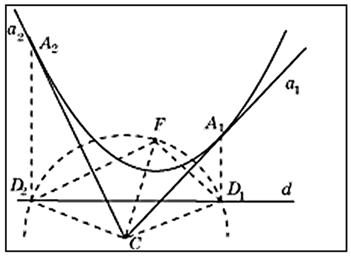
Рисунок 5.

На основании свойств касательной можно выполнить построение касательных к параболе, проведенных из точки P. Пусть парабола задана фокусом F и директрисой d. Используя циркуль и линейку, построим касательную к параболе, проходящую через данную точку C. С центром в точке C и радиусом CF проведем окружность и найдем ее точки пересечения с директрисой d. Если расстояние от точки C до фокуса больше, чем расстояние до директрисы, то таких точек две. Обозначим их D₁ и D₂. Проведем биссектрисы углов FCD₁ и FCD₂соответственно. Прямые a₁ и a₂, содержащие эти биссектрисы являются серединными перпендикулярами к отрезкам FD₁ и FD2 и, значит, будут искомыми касательными к параболе. Для построения точек касания через точки D₁ и D₂ проведем прямые, перпендикулярные директрисе и найдем их точки пересечения

A₁ и A₂ с прямыми a₁ и a₂. Они и будут искомыми точками касания. Через точку C проходят две касательные к параболе.

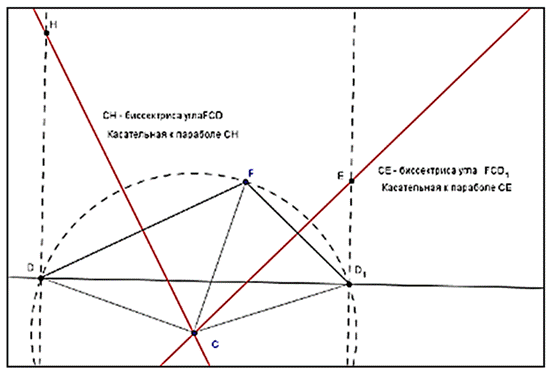
Рисунок 6.

Построение касательных, проходящих через точку С выполнено в ИГС GeoGebra с помощью инструментов: Окружность по центру и радиусу, Отрезок по двум точкам, Пересечение двух объектов, Серединный перпендикуляр.

Заключение

В результате выполнения работы установлено, что:

•геометрическое место точек, являющихся точками пересечения взаимно-перпендикулярных касательных к параболе у = ах².

•касательная к параболе, проходящая через точку А параболы, является прямой, содержащей биссектрису угла, образованного лучом AF, где А — фокус параболы, и перпендикуляром, опущенном из точки А на директрису параболы.

•точки, симметричные фокусу параболы относительно всевозможных ее касательных, расположены на директрисе параболы.

•На основании установленных свойств касательной к параболе выявлены способы построения касательной

При выполнении работы были продемонстрированы возможности применения ИГС GeoGebra, что явилось новизной в исследовании поставленной проблемы.

Список литературы:

1.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. Дополнительные главы к учебнику 9 класса — М.: Вита — Пресс, 2003. — 176 с.;

2.Энциклопедический словарь юного математика. Сост. Савин А.П. — М.: Педагогика, 1985. — 352 с.;