«ЗОЛОТОЕ СЕЧЕНИЕ» В МАТЕМАТИКЕ

Балахничёва Люда

класс 11 «Б», физико-технический лицей, г. Херсон, Украина

Радомская Валентина Александровна

научный руководитель, учитель математики высшей категории, физико-технический лицей, г. Херсон, Украина

В геометрии существует два сокровища — теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем

Иоганн Кеплер

Постановка проблемы. Самым известным математическим сочинением античной науки являются «Начала» Евклида (III век до н. э.), содержащее основы античной математики: элементарную геометрию, теорию чисел, алгебру, теорию пропорций и отношений, методы определения площадей и объемов и др. Именно из «Начал» Евклида к нам пришла следующая геометрическая задача, называемая задачей «о делении отрезка в крайнем и среднем отношении» (золотое сечение), сущность которой сводилась к разделению отрезка АВ точкой С в таком отношении, чтобы большая часть отрезка СВ так относилась к меньшей части АС, как отрезок АВ к своей большей части СВ.

Но задолго до Евклида о золотом сечении, судя по всему, знали еще в древнем Египте, Вавилоне и Китае. Помимо геометрии принцип золотого сечения широко использовался в живописи, скульптуре, при изготовлении музыкальных инструментов и особенно в архитектуре. Строители египетских пирамид, Парфенона, средневековых соборов, Витрувий, Фидий, Леонардо да Винчи, Пифагор, Евклид, Платон, Кеплер и Пачоли, скрипичный мастер Страдивари — вот лишь малая, но представительная часть списка тех, чьи имена так или иначе связаны с историей золотого сечения.

Можно только удивляться тому факту, что в последствии в течение многих столетий ученые не уделяли должного внимания развитию математического аппарата для моделирования «золотого» мира, который существует в реальной действительности, а ведь практическое применение принципов «Золотого сечения» и «Золотого правила», несомненно, будет способствовать развитию нашей цивилизации в правильном направлении.

Цель исследования — рассмотреть гармонию «золотого сечения».

Основной материал. В математике пропорцией (лат. proportio) называют равенство двух отношений: a/b = c/d.

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему (рис. 1):

Рисунок 1. Золотое сечение или деление отрезка в крайнем и среднем отношении

Такая задача имеет решение в виде корней уравнения:

x² — x — 1 = 0,                                                  (1)

единственный положительный корень которого

=1,61803 39887 49894 84820 45868 34365 63811 77203 …

и есть число (константа) золотого сечения.

Как известно, это число называется числом j (PHI) в честь выдающегося греческого скульптора Фидия (Phidias), который широко использовал это уникальное число в своих скульптурах.

Термин «золотое сечение» (aurea sectio) идет от Клавдия Птолемея, который дал это название числу 0,618, убедившись в том, что рост человека правильного телосложения естественно делится именно в таком отношении. Закрепился же данный термин и стал популярным благодаря Леонардо да Винчи, который часто его использовал [3].

Вот первое поразительное свойство j:

 то есть

Такое невозможно ни с одним другим числом.

Вот еще одно удивительное равенство:

то есть:

К уникальным математическим свойствам золотого сечения относятся:

1.  Цепная дробь. Если записать уравнение (1) в виде  а затем все члены тождества разделить на х, то мы придем к следующему выражению:

Далее, раз за разом заменяя х в знаменателе значением (1+1/х), придем к единственной в своём роде цепной дроби:

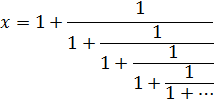
2.  Золотой радикал. Рассмотрим снова тождество  Если взять корень квадратный из правой и левой частей тождества, то получим следующее выражение:  Далее, если в правой части выражения вместо х подставить его же задаваемое выражение, то получим следующее:

 .

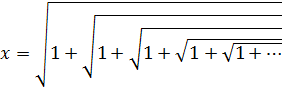3.  Числа Фибоначчи. Используя цепную дробь получим бесконечную последовательность рациональных дробей:

Здесь каждое число в числителе или знаменателе равно соответственно сумме числителей и знаменателей двух предыдущих дробей. В обоих случаях имеем ряды, строящиеся по правилу третьего члена: каждый член последовательности чисел, начиная с третьего, равен сумме двух предыдущих членов [1, с. 3]. Это ряд Фибоначчи, который в простейшем классическом варианте представляет собой бесконечную последовательность чисел Fn:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181 …

Исследуя свойства полученной числовой последовательности, Фибоначчи заметил, что отношения её соседних членов (начиная с пятого) соответствуют условиям гармонического деления. Число, выражающее сумму двух предыдущих, соотносится с большим из них так же, как большее число соотносится с меньшим. Например: .

Золотое сечение можно найти, рассматривая некоторые геометрические фигуры.

Из «Начал Евклида» известен следующий способ геометрического построения «золотого сечения» с использованием линейки и циркуля (рис.2). Построим прямоугольный треугольник ABC со сторонами AB = 1 и ВC = ½. Для начала с помощью линейки отмеряем отрезок АВ. Затем из точки В возводится перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. Треугольник АВС готов.

Рисунок 2. Геометрическое построение золотого сечения

В соответствии с теоремой Пифагора сторона  Проведя дугу DС с центром в точке С до пересечения с отрезком АС в точке D мы получим отрезок 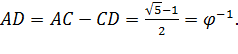 Проведя дугу АD с центром в точке А до её пересечения с отрезком АВ в точке Е мы получим деление АВ в точке Е «золотым сечением», поскольку

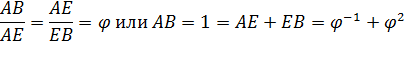
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая равна 38 частям.

Таким образом, хорошо известный в древнем мире простой прямоугольный треугольник с отношением катетов 1:2 мог послужить основой для открытия «теоремы квадратов», золотой пропорции и, наконец, «несоизмеримых отрезков» — трех великих математических открытий, приписываемых Пифагору.

Двумерным символом золотого сечения вправе считаться пентаграмма (пентальфа, пентагерон), обычно понимаемая как пятиугольная звезда, вписанная в правильный пятиугольник (рис. 3). В этой фигуре наблюдается удивительное постоянство отношений составляющих ее отрезков.

Рисунок 3. Пентаграмма

На рисунке 3 AD/AC = AC/CD = AB/BC = AD/AE = AE/EC. Пользуясь симметрией звезды, этот ряд равенств можно продолжить. Все эти отношения равны числу  (1,618...).

Список трёхмерных золотых тел всегда начинается со знаменитых ещё со времен Платона, позже «Начал» Евклида додекаэдра и икосаэдра — двух из пяти платоновых тел (рис. 4), то есть многогранников составленных из однотипных правильных многоугольников.

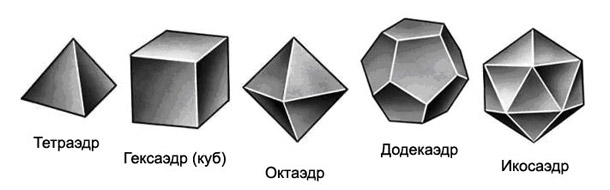
Рисунок 4. Платоновы тела

Известны также золотые призмы, эллипсоиды, ромбоэдры, 13 архимедовых тел — полуправильных многогранников составленных из правильных многоугольников двух или более типов, столько же двойственных им каталановых тел (табл. 1), составленных подобно правильным многогранникам из одинаковых, но уже неправильных многоугольников, а также множество трёхмерных тел менее благородного происхождения [1, с. 2].

Таблица 1.

Примеры архимедовых и каталановых тел [2]

Таким образом, почти половина наиболее важных трёхмерных тел непосредственно причастна к золотой пропорции. Понятно, что через константу  выражаются и другие параметры тел: двугранные углы, радиусы вписанных и описанных сфер, площади граней и всей поверхности, объёмы тел.

Выводы. В современной науке интерес к Золотому Сечению возрос с новой силой. Золотое Сечение оказалось источником новых и плодотворных идей в математике, теоретической физике и кристаллографии, экономике, биологии, ботанике, компьютерной науке, теории кодирования и криптографии. В современной науке сделано ряд выдающихся открытий, основанных на числах Фибоначчи и Золотом Сечении. Два наиболее крупных научных открытия ХХ-го века — квазикристаллы и фуллерены (Нобелевская Премия 1996 г.) основаны на Платоновом икосаэдре и Архимедовом усеченном икосаэдре, главной пропорцией которых является Золотое Сечение.

И наконец, самое, пожалуй, главное — структура ДНК генетического кода жизни, представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная — от Метагалактики и до живой клетки — построена по одному принципу — бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции Золотого Сечения!

Список литературы:

1.Аракелян Г. О мировой гармонии, теории золотого сечения и её обобщениях [Электронный ресурс] — Режим доступа. — URL: http://w.trinitas.ru/rus/doc/0232/013a/2065-ar.pdf

2.Полуправильный многогранник [Электронный ресурс] — Режим доступа. — URL: http://ru.wikipedia.org/wiki

3.Стахов А. Код да Винчи и ряды Фибоначчи / А. Стахов, А. Слученкова, И. Щербаков. [Электронный ресурс] — Режим доступа. — URL: http://e-noosphere.com/noosphere/ru/magazine/Default.asp?file=20060208_Stakhov_Sluchenkova_Scherbakov.htm