КРИВЫЕ ВТОРОГО ПОРЯДКА В КОНСТРУИРОВАНИИ ШВЕЙНЫХ ИЗДЕЛИЙ

Анисимова Олеся

группа 303 ГБОУ СПО СО «Первоуральский политехникум» г. Первоуральск

Ногина Наталья Александровна

научный руководитель, преподаватель математики высшей категории ГБОУ СПО СО «Первоуральский политехникум» г. Первоуральск

Профессия закройщик, которую я получаю, предполагает построение лекал для раскроя, конструирование одежды. При конструировании одежды используются следующие основные элементы графических построений:

·построение базисной сетки;

·определение положения конструктивных точек чер­тежа засечками дуг;

·построение лекальных кривых;

Эти три метода широко используются в практике и изучаются на уроках. Но ч прочитала еще об одном методе: построение кривых второго порядка с помощью проек­тивных дискриминантов. Меня заинтересовали кривые второго порядка, поэтому целью моей работы является рассмотреть некоторые кривые второго порядка и показать, как их использовать в профессии закройщика.

Задачи данной работы ответить на ряд вопросов:

1. Что такое полярная система координат?

2. Как строятся кривые в этой системе?

3. Есть ли интересные кривые в прямоугольной декартовой системе координат?

4.  Возможно ли применение кривых второго порядка в профессии «закройщик»?

1.  Полярная система координат

Полярная система координат задается произвольной точкой (полюсом) О и лучом ОХ — полярной осью. Тогда положение точки М на плоскости определяется двумя величинами: 1) ее расстоянием ρ = |ОМ| от полюса О или полярным радиусом; 2) величиной угла φ, образованного отрезком ОМ с полярной осью ОХ (рис.1). Угол φ считается положительным при отсчете от полярной оси против часовой стрелки.

Рисунок 1. Полярная система координат

Положение точки М заданием ρ и φ определяются однозначно: отрезок ρ — положение точки на луче ОМ, а угол φ определяет направление луча. Однако, угол φ определяется не однозначно, через 2πk, где k — целое число полярный угол повторяется. При этом, расстояние до точки М может быть различным или постоянным. Для устранения неоднозначности в случае повторения значений ρ в качестве полярного угла обычно выбирают наименьший (по абсолютной величине) угол φ, составляемый ОМ с полярной осью, т. е. выбирают φ в диапазоне от π до 2π.

Связь между полярными и декартовыми координатами устанавливается из соотношения между углами и сторонами треугольника ОМА (рис. 2).

х = ρ cosφ; y = ρ sinφ;                  ρ² = х² + у² ;                  tg φ = .

Рисунок 2. Связь полярных и декартовых координат

2.  Кривые второго порядка в полярной системе координат

2.1. Спираль Архимеда

Рассмотрим линию, определяемую уравнением

r = а j,

где: а — некоторая положительная постоянная (коэффициент пропорциональности).

Построим график этой функции при а = 1, для этого найдем несколько её точек, записывая расчеты в таблице.

Таблица 1.

Откладывая полученные значения на соответствующих лучах, получим точки A,B,C,D,E,F, принадлежащие графику функции r = j. Соединяя полученные точки плавной кривой, получим спираль Архимеда (рис. 3). Расстояния между витками одинаковы, так АА₁ = А₁А₂ = А₂А₃

Рисунок 3. Спираль Архимеда

Рисунок 4. Логарифмическая спираль

2.2.    Логарифмическая спираль

Кривая, пересекающая все лучи, выходящие из точки О под одним и тем же углом φ. В полярной системе координат задается уравнением ρ=а е ^{к φ}.

Точка кривой делает бесчисленное множество оборотов вокруг полюса, неограниченно удаляясь от него при φ > 0 (рис.4). Расстояния между витками, по сравнению со спиралью Архимеда не одинаковы! При отрицательных значениях φ кривая совершает бесчисленное множество оборотов вокруг полюса, безгранично к нему приближаясь, но никогда его не достигая, т. е. полюс для логарифмической спирали является асимптотической точкой.

2.3.    Лемниската Бернулли

Лемнискатой называется геометрическое место точек М, произведение расстояний МF₁ · МF₂ = а², т. е. величина постоянная. Уравнение Лемнискаты в декартовых координатах имеет вид: (х² + у²)^{2 —} 2а²(х² — у²) = 0

Исследовать кривую по этому уравнению довольно сложно. Если же перейти к полярным координатам, то уравнение примет более простой вид:

ρ² = b² cos 2φ.

Начало координат — узловая точка с касательными у =  х, таким образом, кривая проходит через полюс при φ =  + , к Z.

Рисунок 5. Лемниската Бернулли

2.4.    Улитка Паскаля

Улиткой Паскаля называется кривая, определяемая уравнением

ρ= а cosφ + l,

где: а — диаметр круга.

Вид кривой зависит от величин а и l: при а > l получаем кривую с внутренней петлей, при а = l кривая имеет точку возврата — начало координат (рис. 6), в этом случае кривую называют кардиоидой.

Рисунок 6. Улитка Паскаля

2.5.    Розы

Розы — плоские кривые, уравнения которых в полярных координатах имеют вид

ρ = α sin κφ,

где: α и κ — постоянные.

Если κ = m/n — число рациональное, то роза — алгебраическая кривая четного порядка. Порядок этой кривой равен m + n, если m и n — нечетные числа, и равен 2(m + n), если одно из чисел m и n — нечетное. Вся кривая расположена внутри круга радиуса α, состоит из одинаковых лепестков. Если κ — целое, то роза состоит из κ лепестков при κ нечетном (рис. 7) и из 2κ лепестков при κ четном (рис. 8).

Рисунок 7. Трехлепестковая роза

Рисунок 8. Четырехлепестковая роза

3.  Кривые второго порядка в прямоугольной декартовой системе координат

В прямоугольной декартовой системе координат чаще всего рассматриваются окружность, эллипс, гипербола и парабола. При этом уравнения этих линий приведены к каноническому (типовому) виду.

(х — а)² + (у — b)² = R² — окружность

х²/а² + у²/в² = 1 — эллипс

х²/а² — у²/в² = 1 — гипербола

х² = 2p y — парабола.

В школьном курсе математики не упоминается о других кривых — циклоидах, эпициклоидах и гипоциклоидах, а эти линии невероятно красивы!

Циклоида — это линия, которую описывает закрепленная в плоскости круга точка, когда этот круг катится (без скольжения) по некоторой прямой.

Уравнение циклоиды в параметрической форме:

х = а(t — sin t);                      y = a(1 — cos t),

где: а — радиус окружности

Циклоида называется обыкновенной, если точка взята на окружности (рис. 9. линия 1), укороченной, если точка взята внутри круга (рис. 9. линия 2), удлиненной, если точка — вне круга (рис. 9. линия 3).

Рисунок 9. Циклоиды

Эпициклоида получается при качении круга по окружности внешним образом, гипоциклоида — внутренним образом. В декартовой системе координат эти линии задаются параметрически:  

Эпициклоида (рис. 10)

x = (А + а)cosφ — a cos (A+a)φ/a

y = (А+ а)sin φ — a sin (A+a)φ/a

гипоциклоида (рис. 11) получается при замене а на (-а).

Рисунок 10. Эпициклоида

Рисунок 11. Гипоциклоида

5.  Применение кривых второго порядка в профессии «закройщик»

Спираль Архимеда используется в качестве линии, позволяющей разделить заданный угол на любое количество равных частей. В некоторых готовальнях в старину в состав рабочих инструментов входила металлическая пластинка с тщательно выгравированной на ней спиралью Архимеда. С помощью такого приспособления было нетрудно разделить угол на несколько равных частей.

Спираль Архимеда находит широкое применение в механике, например в кулачковых механизмах, которые преобразуют вращательное движение кулачка в поступательное движение толкателя. Представление о спирали Архимеда дают звуковая дорожка на грампластинке, торец рулона обоев, шарик на нитке, разматывающейся от стержня. Эту кривую получаем при равномерном наматывании ниток на шпульку в механизме швейных машин.

Спираль Архимеда дает линию кроя декоративного элемента — волан. Этим способом можно нарисовать волан прямо на ткани и выкроить его с минимальными отходами ткани. Таким способом можно из небольшого кусочка ткани выкроить волан достаточно большой длины. Этот способ хорош, если нужны воланы для оформления платья или юбки с ассиметричной линией кроя — то есть в тех случаях, когда равномерность и одинаковость завихрений волана не важна. На рисунке 12 представлен орнамент ткани с применением спирали Архимеда.

Рисунок 12. Орнамент ткани со спиралью Архимеда

Многие вещи в природе могут дать представление о логарифмической спирали, например раковина улитки последовательные витки которой не одинаковы, а все более и более утолщаются. Семена подсолнуха расположены в соцветии по дугам логарифмической спирали, длина листьев растений от нижних к верхним часто подчинена логарифмическому закону.

По логарифмическим спиралям закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система.

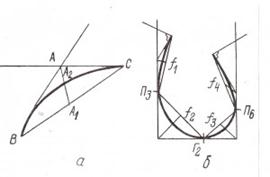
В основу алгоритма графических построений, осуществляемых в автоматизированном режиме, положен метод проективных дискриминантов кривой. Такой способ графического построения кривых второго порядка является более сложным и в то же время более точным способом оформления криволинейных срезов деталей. Проективный дискриминант (f) ха­рактеризует степень кривизны кривой линии. Он определяется отношением отрезка А₁А₂, отсекаемого кривой на медиане тре­угольника АВС, образованного касательными к кривой в на­чальной и конечной точках, и хордой ВС, к длине медианы АА₂  f = А₁А₂/АА₂

Пример использования проективных дискриминантов (f₁ = f₄ = 0,5 и f₂ = f₃ = 0,42) для построения линии среза проймы по­казан на рисунке 13.

Рисунок 13. Построение линии среза проймы

Кривые второго порядка широко применяются в построении орнаментов кружева. Вот несколько примеров: на рисунке 14, а) мы видим гипоциклоиду в качестве основного мотива; на рисунке 14, б) листья образуют логарифмическую спираль; на рисунке 14, в) — трехлепестковые розы.

а)                                                     б)

в)

Рисунок 14. Примеры кривых второго порядка в орнаментах кружева:

а) гипоциклоида; б) логарифмическая спираль; в) роза

6.  Заключение.

В своей работе я рассмотрела полярную систему координат, построила некоторые кривые второго порядка в этой системе и декартовой прямоугольной системе координат. Рассмотрела применение кривых второго порядка в профессии «закройщик».

Список литературы:

1.Выгодский М.Я. Справочник по высшей математике. — М., 1973 г. — 872 с.

2.Полный курс современного рукоделия. — Издательство: Харвест, 2007 г, 336 с.

3.Радченко И.А. Конструирование и моделирование одежды на нетиповые фигуры. Учеб пособие. — издательство «Академия» 2009 г.