МНОГОГРАННИКИ

Донгак Кузел

Класс 10 «б», ГБОУ Аграрный лицей Республики Тыва

Серен-оол Саяна Александровна

научный руководитель, педагог первой категории, преподаватель математики,

ГБОУ Аграрный лицей Республики Тыва

Введение

Симметрией связаны представления о красоте с давних времен. Особенно это касается правильных многогранников. Многогранники характерны для философии Платона, в честь которого получили название «платоновы тела». О многогранниках Платон писал в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух – октаэдру, вода – икосаэдру, а огонь – тетраэдру. Евклид математически полностью описал правильных многогранников XIII книге Начал.

Так же известен ряд совершенных тел, получивших название «полуправильных многогранников» или «Архимедовых тел». Эти «Архимедовы тела» делятся на несколько групп, одну из которых составляют пять многогранников, получившихся из «Платоновых тел»в результате их усечения. Для «Платоновых тел» усечение выполняется таким образом, что и получающиеся новые грани и остающиеся части предыдущих тел будут правильными многоугольниками. Удивительная красота форм многогранников невольно наталкивает на мысль: «А что, если их модели сделать не по их разверткам, а используя технику оригами?»… Искусство оригами существует уже несколько сотен лет. Искусство складывания из бумаги своими корнями уходит в древний Китай, где была изобретена бумага. Первоначально оригами использовалось в религиозных обрядах. На протяжении многих лет этот вид искусства был доступен только представителям высших сословий, где признаком хорошего тона было владение техникой складывания из бумаги. После второй мировой войны оригами вышло за пределы Востока и попало в Америку и Европу, где сразу обрел своих поклонников.

Актуальность

Оригами может быть интересно людям разного возраста. При помощи оригами я получаю возможность создавать своими руками красивые геометрические фигуры из бумаги. Используя оригами, можно сделать что-то оригинальное своими руками из бумаги. Оригами это всегда красиво и оригинально.

Цели и задачи: вписать в модуль Сонобе тетраэдр.

Методы исследования:

1.Изучить историю возникновения оригами, необходимый материал, приемы и технологию выполнения

2. Изучить лист бумаги, выполнив необходимые измерения.

3.Изучить каскадное вписывание многогранников.

4.Решить ряд задач.

5.Выполнить каскадное вписывание в модуль Сонобе тетраэдра изготовить образцы изделий в технике оригами.

Гипотеза: Возможно, для того, чтобы выполнить каскадное вписывание многогранников, необходимо вычислить площадь необходимой бумаги для тетраэдра и для гексаэдра, выполнить необходимые измерения их ребра.

1.Красота и сложность многогранников.

“Правильных многогранников так мало,но это весьма скромный по численностиотряд сумел пробратьсяв самые глубины различных наук”.(Л.Кэрролл). [8,9]

«Теория многогранников, в частности выпуклых многогранников,– одна из самых увлекательных глав геометрии»(русский математик Л.А. Люстернак). [8,9]

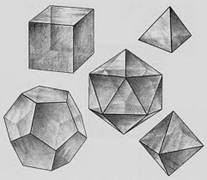
Правильный многогранник – это многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. [6, стр. 32]

Известно 5 правильных многогранников.Для того чтобы получить какой-нибудь правильный многогранник, в каждой вершине должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником. Сумма плоских углов многогранного угла должна быть меньше 360^о. Перебирая возможные целые решения неравенств: 60к < 360, 90к < 360 и 108к < 360, можно доказать, что правильных многогранников ровно пять (к - число плоских углов, сходящихся в одной вершине многогранника).

«Теорема Эйлера

Для любого выпуклого многогранника справедливо соотношение:

Г+В-Р=2,

где Г-число граней, В-число вершин, Р- число ребер данного многогранника.

Грани + Вершины - Рёбра = 2.»[6, стр.29]

 Названия правильные многогранники связано с числом их граней:

1.тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре,

2.гексаэдр (куб) имеет 6 граней, в переводе с греческого "эдрон" - грань,"гекса" - шесть;

3.октаэдр - восьмигранник, в переводе с греческого "окто" - восемь;

4.додекаэдр - двенадцатигранник, в переводе с греческого "додека" двенадцать;

5.икосаэдр имеет 20 граней, в переводе с греческого "икоси" - двадцать.

2.Процесс каскадного вписывания

Правильные многогранники можно вписывать друг в друга. При этом возможны следующие случаи:

1.Вершинами вписанного многогранника являются некоторые вершины описанного многогранника.

2.Вершинами вписанного многогранника являются середины ребер описанного многогранника.

3.Вершинами вписанного многогранника являются центры граней описанного многогранника.

4.Серединами ребер вписанного многогранника являются центры граней описанного многогранника.

5.Центрами граней вписанного многогранника являются некоторые центры граней описанного многогранника.

Последовательное вписывание друг в друга правильных многогранников называется каскадным вписыванием.

 Правильные многогранники можно вписывать друг в друга. В куб можно вписать октаэдр. Центры граней куба образуют вершины вписанного в него октаэдра. Центры граней октаэдра образуют вершины вписанного в него куба. Многогранники, обладающие таким свойством, называются взаимно двойственными. Таким образом, октаэдр и куб - взаимно двойственные многогранники (рис. 1, а, б [8, 9 ])

 Взаимно двойственными правильными многогранниками являются додекаэдр и икосаэдр. Центры граней додекаэдра находятся в вершинах вписанного в него икосаэдра. И наоборот, центры граней икосаэдра служат вершинами вписанного в него додекаэдра (рис. 2, а, б[8,9]).

Правильные многогранники вписываются друг в друга не только таким способом, о котором сказано выше. Например, в куб можно вписать тетраэдр. При этом вершины тетраэдра будут лежать в вершинах куба (рис. 3[8,9]). Куб можно вписать в додекаэдр так, чтобы вершины куба лежали в вершинах додекаэдра (рис. 4[8,9]). Известно, что при вписывании одного правильного многогранника в другой, вершины первого лежат на серединах ребер второго. Такими многогранниками являются тетраэдр и вписанный в него октаэдр (рис. 5[8,9 ]).

Существует еще один способ: середины ребер вписываемого многогранника лежат в центрах граней описываемого. Для этого можно построить на гранях куба отрезки, параллельные ребрам и середины которых лежат в центрах граней. Таким отрезком является отрезок AB (рис. 6[8,9]). Если, соединить концы этих отрезков, как показано на рисунке 6, то получится многогранник, гранями которого являются двадцать треугольников и в каждой вершине сходится пять ребер. Для того, чтобы этот многогранник был икосаэдром, нужно подобрать такую длину отрезка AB, чтобы все его ребра были равны.

Пусть ребро куба равно 2. Обозначим длину отрезка AD, являющуюся серединой АВ, через x. Вычислим длину ребра BC. На рисунке 6 изображено сечение куба, перпендикулярное AB и проходящее через его середину D.

 CD² = 1 + (1 – x)² = x² – 2x + 2. BC² = BD² + CD² = 2x² – 2x + 2. Из условия AB = BC получается уравнение 4x² = 2x²– 2x + 2.
Откуда находится x = , т. е. x равно золотому отношению.

Теперь, для того, чтобы сделать мне каскадное вписывание тетраэдра в гексаэдр, необходимо научиться из бумаги конструировать тетраэдр и модуль Сонобе [приложение: рис 1-4, рис. 6-11[8,9]], затем, изучив бумагу, решить ряд задач.

Задача 1. Найдите ребро тетраэдра, вписанного в куб с ребром х.

Рис.*[8,9]

Решение. Так как ребро у тетраэдра является диагональю грани куба, а грань куба – есть квадрат, то диагональ является гипотенузой прямоугольного треугольника внутри квадрата. По теореме Пифагора: += . y=

Ответ:

Задача 2. Вычислить, используя 1 модуль Сонобе, отрезок равный ребру тетраэдра, если берется квадрат из бумаги формата А4, т.е. сторона квадрата равна 21 см.

Решение. На 4 шаге [приложение: рис. 5] заметим, что ребро тетраэдра, вписанного в куб с данным размером, совпадает с длиной, равной половине длины куба. Следовательно, отрезок, равный ребру тетраэдра, составляет: 21:2=10,5(см).

Ответ: 10,5 см.

Задача 3. Исследовать, какого размера нужно брать квадрат, чтобы ребро тетраэдра, вписанного в искомый куб, составляло 10,5 см?

Решение. Возьмем бумажный квадрат со стороной 21 см. Используя метод оригами, будем строить тетраэдр. На 3шаге [приложение: рис. 5] заметим, что длина ребра тетраэдра равен длине диагонали куба, куда будет вписан тетраэдр: 10,5 см.

Вывод: чтобы построить каскадное вписывание тетраэдра в гексаэдр по методу оригами, нужно брать квадратный лист одного итого же размера.

Задача 4. Выполнить модель каскадного вписывания тетраэдра в гексаэдр, используя модуль Сонобе , метод оригами, результаты 1-3 задач.

Решение. См. приложение рис. 12-18.

Заключение.

В результате моего исследования можно сделать вывод, что моя гипотеза подтвердилась. Вывод заключается в том, что искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения. Занимаясь оригами, я вышел за границы стандартной программы по математике и познакомился на практике с элементами геометрии в пространстве, а также выяснил, что оригами выступает как иллюстративный материал при проведении исследовательской работы.

По началу выполнения данной исследовательской работы мне было трудновато, но потом я прочитал определённую литературу и стало мне гораздо легче и понятнее. При завершении исследования работы я посмотрел на мир иными глазами. Оказывается, в этом мире есть такие чудеса и красоты математики, о которых я и не задумывался.

Строить модели мне очень понравилось, особенно используя оригами. Планирую продолжить моделирование каскадных вписываний многогранников в дальнейшем.

Приложение

Список литературы:

1.Журнал «Наука и техника»

2.Журнал «Квант», 1973, № 8.

3.Журнал «Математика в школе», 1994, № 2; № 3.

4.Ковалев Ф.В. Золотое сечение в живописи. К.: Высшая школа, 1989.

5."Математика - Энциклопедия для детей" М.: Аванта +, 1998

6.Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995

7.Стахов А. Коды золотой пропорции.

8.http://festival.1september.ru

9.http://ru.wikipedia.org